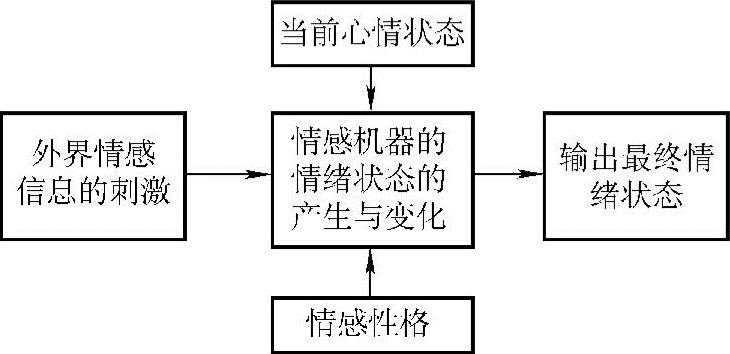
图5-10 情绪状态刺激转移过程基本模型框图

相对于情绪状态自发转移过程，情绪状态刺激转移过程则显得更加重要。根据心理学理论，在有外界情感信息刺激的情况下，情感状态主要体现在情绪的变化，而情绪的变化又受到多方面的影响，概括地说，主要由外界情感信息的刺激（类型、强度）、当前心情状态以及情感性格三个因素共同作用而发生影响，其基本的模型框架如图5-10所示。

隐马尔可夫链（Hidden Markov Model，HMM）是在马尔可夫链的基础上发展起来的。由于实际问题比Markov链模型所描述的更为复杂，观察到的事件并不是与状态一一对应，而是通过一组概率分布相联系，这样的模型就称为HMM。它是一个双重随机过程，其中之一是Markov链，这是基本随机过程，它描述状态的转移。另一个随机过程描述状态和观察值，不像Markov链模型中的观察值和状态一一对应，因此不能直接看到状态，而是通过一个随机过程去感知状态的存在及特性。因而称之为“隐”Markov模型，即HMM。

一个HMM可以由下面的五个参数描述：

N：模型中Markov链状态的数目。记N个状态为θ₁，…，θ_N，记t时刻Markov链所处状态为q_t，显然q_t属于（θ₁，θ₂，…，θ_N）。

M：每个状态对应可能的观察值的数目，记M个观察值为V₁，…，V_M，记t时刻观察到的观察值为O_t，其中O_t属于（V₁，…，V_M）。

π：初始位置概率矢量

π=（π₁，…，π_N） （5-6）式中 π_i=P（q_t=θ_i） 1≤i≤N

A：状态转移概率矩阵

A=（a_ij）_N×N （5-7）式中 a_ij=P（q_t+1=θ_j|q_t=θ_i） 1≤i，j≤N(www.daowen.com)

B：观察值概率矩阵

B=（b_jk）_N×M （5-8）式中 b_jk=P（O_i=V_k|q_t=θ_j）1≤j≤N，1≤k≤M

由此，可以记一个HMM为

λ=（N，M，π，A，B） （5-9）

或简写为

λ=（π，A，B） （5-10）

更形象地说，HMM可以分为两个部分，一个是Markov链，由π、A描述，产生输出状态序列；另一个是随机过程，由B描述，产生的输出为观察值序列，如图5-11所示，T为观察值时间长度。

图5-11 HMM结构示意图