传统的强化传热的方法虽已取得相当广泛的应用，但是它们普遍存在一个相同的问题，即在传热强化的同时，流动阻力（或功耗）也相应地增加，甚至增加得更多。这就大大限制了它们工程应用的价值和范围。当前强化技术发展的另一不足之处是，它们基本上是现有技术的改进，缺乏一些基于新概念的创新性的传热强化技术。为此我国学者过增元院士在研究对流换热强化时，提出了著名的场协同原理。下面对强化对流换热的场协同原理予以简要介绍，更详细的介绍参见参考文献［1］。

1.对流换热的物理机制

从对流换热的物理机制可知，由于流体的宏观运动能携带能量，所以对流换热的热量传递速率高于纯导热时的传递速率。如果从另一角度来审视对流换热的物理机制，即将对流换热看作有流体运动时的导热，则可得到一些有趣的结论。

为简单起见，以二维平板层流边界层问题为例（见图2-1（a））。图中，U是来流速度，来流温度Th高于平板温度Tc，并把它与具有内热源的两平行平板之间的导热（见图2-1（b））相对比，其中温度Th的平板处为绝热的。由于流体流经边界层中某一元体时将把热量留在元体中，起着热源的作用，所以它们温度剖而的形状很类似。相应的能量守恒方程如下：

层流边界层的能量守恒方程

导热的能量守恒方程（忽略x向的导热）

其中λ是流体介质的导热系数，ρ是密度，cp是定压比热容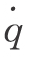，是内热源强度，即单位时间、单位体积所产生的热量。

图2-1　平板层流边界层流动示意图

无论是从温度剖面的形状，还是从两式的对比，均可认为式（2-3a）中的对流项可以看作源项，所以对流换热可以比拟为具有内热源的导热问题，只不过式（2-3a）中的源项（或对流项）是流体运动速度的函数。方程两边在讨论域中积分后得

其中δ1，x代表x处的热边界层厚度。

方程（2-4b）的左边是两平板间x处截面处热源的总和，右边是x处的壁热流。显然，该截面的热源强度愈高，该处的壁热流就愈大。因为热源释放出的所有热量必须从冷板传出，这就是导热问题中的源强化传热概念。

方程（2-4a）的左边是x处边界层中对流热源项的总和，右边则是x处的壁热流，它正是我们想要强化（或控制）的对象。显然对流源项总和值愈大，则对流换热的强度愈高。这同样属于源强化。对于流体加热固壁，热源的存在是换热强化。如果存在热汇，则它将减弱换热的强度。反之，当流体冷却热壁时，热汇时换热强化，而热源则使换热弱化。从式（2-4a）可知，当流体温度高于固壁温度时，流体流动相当于热源；当流体温度低于固壁时，流体流动相当于热汇。

虽然上述分析和结论是基于二维层流边界层问题，但过增元院士证明对更普遍的对流换热问题它同样适用。为了探索强化对流换热的途径，过增元院士将式（2-4a）左边的对流项改写成矢量形式：

其中U是流体的速度矢量。然后再引入无因次变量：

将式（2-6）代入式（2-5）并进行整理后得无因次关系式：

其中Rex、Nux的定义与通常边界层流动分析中相同，而被积因子则可写成

其中β是速度矢量和温度梯度矢量（热流矢量）的夹角。从式（2-7）、式（2-8）可以看到，要使换热强化，有三种途径：①提高Re数，例如增加流速，缩小通道直径等；②提高Pr数，改变流动介质的物理性质，例如增加流体的比热容或黏度，可以增大Nu数；③增加无因次积分值。前两种途径是通常采用的，而第三条强化换热的途径则是我国过增元院士首次提出的。(www.daowen.com)

上述无因次积分的物理意义就是在x处热边界层厚度截面内的无因次热源强度的总和。可以想象，热源强度愈大，换热强度就愈高。这个积分的数值一般与流动、物性因素等有关。也就是说，它是Re、Pr的函数，即

一般来说，由于其复杂性，很难写出积分I的分析表达式。但是有一点是明显的，即提高被积函数的数值，就能增加I值，从而强化换热。因为被积函数是两个矢量的点积，它不仅与速度、热流的绝对值有关，还取决于它们夹角的大小。也就是说，在速度、温度梯度一定（或Re、Pr不变）的条件下，减小它们之间的夹角（β＜90°时），就能提高积分I的数值，从而使Nu增大，即强化换热。因此当β＜90°时，通过减小速度矢量与热流矢量的夹角是强化换热的一种新的途径。

2.对流换热的场协同

对于对流换热问题，有流体流动时必然存在着一个流体速度场（或称流场），它是一个矢量场。此外，流体的温度是不均匀的，还存在一个流体温度梯度场。当ρ、cp、λ给定时，速度场和温度梯度场的特性就确定了边界上的热流，即确定了边界上的对流换热系数。所以对流换热域中存在着两个矢量场：

（1）速度场　　　　　U（x，y，z）

（2）温度梯度场　　　∇T（x，y，z）或者三个标量场：

（1）速度绝对值　　|U|（x，y，z）

（2）温度梯度绝对值　|∇T|（x，y，z）

（3）夹角余弦场　　　cosβ（x，y，z）

在前述分析的基础上，过增元院士提出了对流换热的场协同概念。在流速和流体的物理性质给定的条件下，对流换热强度不仅取决于速度场和温度梯度场本身，而且取决于它们之间的夹角。即不仅取决于速度场、温度梯度场、夹角场的绝对值，还取决于这三个标量值的协同。具体而言，速度场与温度梯度场的协同体现在以下二个方面：

（1）速度矢量与温度梯度矢量的夹角余弦值尽可能大，即两矢量的夹角β尽可能小（β＜90°时）或β尽可能大（β＞90°时）；

（2）流体速度剖面和温度剖面尽可能均匀（在最大流速和温差一定条件下）；

（3）尽可能使三个标量场中的大值与大值搭配，也就是说，要使三个标量场的大值尽可能同时出现在整个场中某些域上。

过增元院士将对流换热的场协同原理具体表述为：“对流换热的性能不仅取决于流体的速度和物性以及流体与固壁的温差，而且还取决于流体速度场与温度梯度场间协同的程度。在相同的速度和温度边界条件下，它们的协同程度愈好，则换热强度就愈高。”

经过我国科学工作者努力，对流换热的场协同原理不但得到了实验验证，而且可以从边界层（抛物线形）流动推广至回流（椭圆形）流动，从层流流动推广至湍流流动，从稳态流动推广至一维瞬态流动，从单股流流动推广至两股（多股）流换热器，从无外场的热对流推广至磁场作用下的热对流。理论分析还证明，现有的许多强化对流换热的方法也是符合场协同原理的。现在对流换热的场协同原理已经得到国内外学者的公认，依据场协同原理提出的一些强化传热的方法也已获得工业应用。