在前面几章中，我们已经介绍过很多图表表述方法和图表推理方法。通过多种不同的图表技术，不同类型的应用以及大量的图表推理方法来帮助我们推知问题的解决方法。在这点上，倒退一步以反映出图表推理的主要内容和潜在内涵是非常有用的。那么，图表有哪些通用的规范呢？我们又该如何评判图表的质量？（在回答这些问题的过程中，又有哪些是图表方法的局限或者难点？）如何评估图表的有效性？我们能否将从本书中学到的图表推理技术推广到更多类型？通过对这些问题以及其他问题的回答，我们将会获得对于图表推理和其他更大问题的更广阔前景。在本章中，将提供一种理解图表推理的框架。

首先，我们考虑一些图表的通用规范是什么。各种图表表示法都有许多共同点。第一，相对于语句（语言）表示法，它们都是可视化的图形。这样，就使索引位置在一个平面上成为可能——这就意味着相关的信息可以组合在一起，并按主旨排列。这也使得系统中各种组件的连接可以可视化表示。由于高度的可视化，图表表示法可以利用人类视觉信息处理系统，使得感性的推论更加容易。另一方面，这是我们用语句表示法无法实现的（或者实现起来异常困难）。

图表主要但不总是由几何图形通过直线和箭头相互连接而成（一个重要的例外是维恩图，它是通过重叠圆圈而不是直线连接表示了集合之间的关系）。其中几何图形可以表示多种事物：人、物、概念、事件、活动、决策点、集合、行为、步骤等，几乎所有类型的实体均可建模。同一个图表中的不同形状用来表示不同事物。例如，在决策树中，方块表示决策点，圆圈表示偶然事件；在基本流程图中，矩形表示行为过程，菱形表示决策点。多年以来，图形化工具中已将各种图形代表的意义形成统一的规范。总的来说，与各自独立的标准相比，这种统一的规范要好得多。

如第3章中所介绍的，直线用来表示图表中两个物体的连接。而根据不同的图表类型，直线也有不同的含义，主要包括以下6种连接类型：

1）事物连接（拓扑关系）；

2）时间先后（时序关系）；

3）某一类型（分类关系）；

4）某一部分（成分关系）；

5）相关涉及（关联关系）；

6）起因/影响（因果关系）。

直线可以是直接的，也可以是间接的。箭头通常用来表示直接关系。某些类型的连接总是直接的，比如上述的时序关系、分类关系、成分关系以及因果关系。举例来说，因果关系的连接总是描述为一种直接关系，其中原因在开始的部分，而结果在直线中箭头指向的另一端。(www.daowen.com)

在拓扑关系连接中，系统拓扑框图的连接可以是直接的，也可以是间接的。例如，在液压系统中，连接可以表示水管如何连接到系统组件（如水泵、水库、水阀等）。若水流方向是唯一的，则连接就是直接的。另一方面，在其他的物理系统中，组件之间的相互连接并没有一定的方向。例如在图3-3中，图示了计算机网络中的组件是如何连接的。信息传向各个方向，因此没有直接的连接方式。

在关联关系的连接中，同样可以有直接连接，也可以有间接连接。图3-14是一个语义网络，用来阐述《哈姆雷特》中所有角色的相互关系。其中一些关系是单向的，而另一些关系则是双向的。图9-1为原图的一部分。

在此语义网络中，表示“兄弟”和“夫妻”的连接是双向的（适用于两个方向），而连接“谋杀”（克劳迪亚斯杀害哈姆雷特国王）以及“痛恨”（哈姆雷特王子痛恨克劳迪亚斯）都是单向的。其中双向关系就是间接关系，此时箭头很容易就会忽略掉。

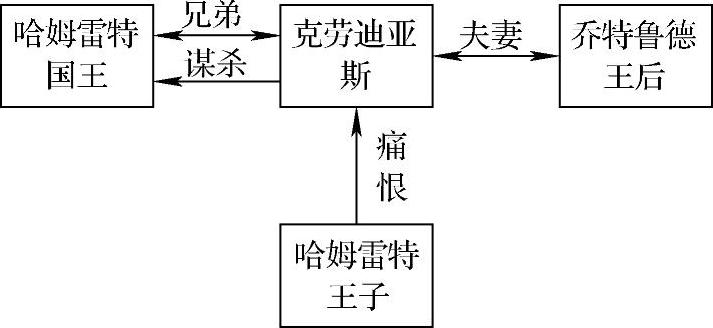
图9-1 语义网络中的单向和双向关系

一般说来，单一的图表一般仅仅包含一种类型的连接。因果图中包含一个因果关系的网络（起因/影响连接），一个系统的拓扑图将包含系统组件之间如何连接（拓扑连接）的描述，流程图用来描述事件的时序进展（时序关系）。然而，如果必须在单一的图表中使用多种类型的连接去进行建模，则必须使用标注来区分不同类型的连接。例如，图3-16是一个使用两种连接方式的实体关系图：一种用来显示基数，另一种用来显示连接类型。为了避免标注含糊不清，通常使用箭头（未填充的）来表示连接类型。有时图表中有隐含的省略箭头的直线。第3章中介绍的决策树就是一个很好的例子（见图3-24和图3-26）。决策树总是从左往右读取，因此没有必要在图表中添加箭头。有时图表是从上到下读取，因此箭头也可以忽略。例如，分层结构，包括组织结构图，继承体系以及组成模式都不会因为移除箭头使得清晰度丧失。但是，当相互关系的方向出现歧义时，就应该在图表中添加箭头（一些图示化工具为了表示的正确性，在所有的分层结构中都添加了箭头表示）。

这实际上就是基本图表中所需了解的全部内容。毕竟，这确实是一个很简单的概念：它由各种图形通过直线直接或间接的相连而成（正如已经指出的，简单的定义也存在一些例外情况）。通过这个基本的描述，说明图表具有呈现各种各样的类型并适用于不同的应用领域的能力。

有时在匆忙中构造的图表，可以用内部表示法帮助我们理解现实世界。第2章中我们学习了有时候人类如何形成像脑海中的图表一样的构思模型。我们形成构思模型去帮助我们理解系统组件是如何互相联系的（内部连接），或者我们形成构思模型去批出一个新系统与我们所熟悉的事物是如何相似或可比拟（外部连接）。由于内部表示是在人的脑海中形成，因此受到人类思想以及短时记忆的局限，其本身可能是不正确的、不完整的、不一致的、不稳定的，甚至是充满迷信和偏见的。

由于内部表示法的这些局限，我们可能将图表变换成某种形式的外部表示。最典型的情况就是在纸上或者是计算机文件中绘制图表。如此一来，我们就可以构建相比于内部表示法更加准确的图表。随着时间推移，我们还可以改善图表，使其对于目标系统的描述更加完整、更加准确、更加一致。由于我们将图表储存于一些外部设备，因此我们可以保留其以便未来的使用和参考，而不是依靠我们的短期记忆。并且，由于我们将图表表示存储于计算机中，就可以进一步通过程序对图表做出各种不同的修改和操作。图形表示的未来就在于智能的用户界面，使得图表可以更加动态有效的使用。