近些年来，作为处理不确定信息的一类方法，贝叶斯网络在人工智能领域得到了广泛的应用。这一概念最初是由Judea Pearl在1985^[9]年提出，是用来反映输入信息的主观性质和根据实际事件的观测利用贝叶斯定理去更新相关概率。

贝叶斯网络的设计思想和实验方法并不太容易理解，因为它们需要深奥的概率论和数学方面知识。这一部分将对于概率论了解有限的人，提出一系列通俗易懂的基本概念（如果你可以回顾起上一部分中的条件概率和基本概率计算的知识，那么也就可以掌握这部分的概念）。希望进一步深入彻底了解贝叶斯网络的读者，请查阅其他相关资料，以获得更深刻的理解和掌握^[10]。

我们可以将一个贝叶斯网络想象成一个用来表示因果关系的分析图（或者贝叶斯网络也可以表示成一个信度网络，用来表示影响假设信度的因素）。图8-11是一个简单的贝叶斯网络示例，其中节点用长方形表示，代表变量。在图中所有变量均为离散变量，只有两个可能的值：是或否。在更复杂的应用中，变量可能呈现出多于两个的离散值，例如恶劣天气可以假定为：（1）非常恶劣；（2）恶劣；（3）有点恶劣；（4）不恶劣四种。当然，也可以是连续值，例如飞机延误可以看作飞机迟到的小时数，从0到无穷大。为了简化问题，后面为了简化条件概率的计算，我们只考虑具有两个可能值的离散节点。

贝叶斯网络中的定向链接用来指定变量间的因果关系或影响关系。在图8-11中，机械故障和恶劣天气都可能导致飞机延误。同样地，恶劣天气也可能导致飞机延误和道路危险，从而导致约翰迟到（若约翰是驾车，则更有可能会因为危险的道路条件而工作迟到）。

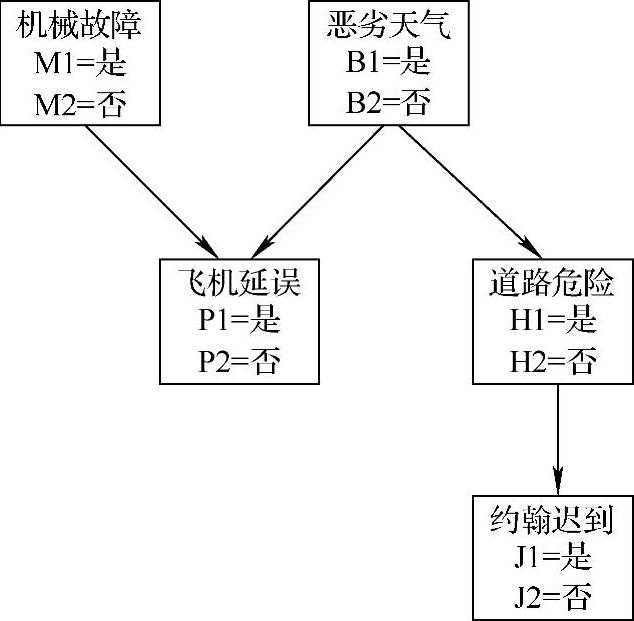
图8-11 简单的贝叶斯网络

在因果关系连接中，对于节点的标注非常重要（见图8-11），但并不是绝对确定的。例如，机械故障与/或恶劣天气的出现都不会必然导致飞机延误，但却肯定会增加飞机延误事件出现的几率。因此，为了表示这种不确定性，我们需要为每个节点分配相应的概率，用以表现某一特定事件发生的可能性。

此外，我们希望能够根据对事件实际的观测数据来更改其相应的概率。例如，我们假设发现飞机确实发生延误。根据直觉，应该考虑观测数据来修改系统中网络节点的参数。特别是我们预计机械故障和天气恶劣的概率会增大。不仅如此，我们也预计道路危险和约翰迟到的概率也会增大（根据天气恶劣概率增大的事实）。贝叶斯推理的真正作用就是它可以基于互联结点的结构，使概率的传播成为可能。接下来我们给出一个特例，用来说明贝叶斯网络如何根据新证据来更新概率。

处理概率推理问题的一种方法是详细指定整个贝叶斯网络的联合概率分布。这里我们提出联合概率分布的意义是什么？在我们继续贝叶斯推理的讨论之前，先花一些时间来看一个联合概率的简单示例。

定义一组随机变量（X₁，X₂，…，X_n）的联合概率分布为P（X₁，X₂，…，X_n）。对于两变量的情况，我们假设这两个随机变量为X和Y，可以使用概率表来详细描述一个离散的两变量的分布情况。假设某一大学有三种宿舍类型，用X表示这三种宿舍：宿舍1、宿舍2和宿舍3。其中宿舍1中男女学生各有一半，宿舍2中全是男生，宿舍3中全是女生。用Y表示学生性别：男生和女生。我们可以将其联合概率分布表示成表8-2的形式：

注意到表格中概率总和为1：

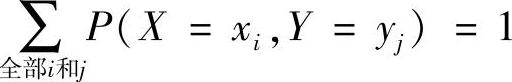
表8-2 关于宿舍类型（X）和性别（Y）的联合概率分布

我们可以将某一特定的联合概率表述为P（X=宿舍2，Y=男生）=0.40（大学中有40%的学生住在宿舍2中，并且是男生）。我们也可以对表格中行或列的概率求和以获得其边缘概率。例如，学生是女生的边缘概率可以通过求取表格中第二行的和得到：

P（Y=女生）=0.15+0.00+0.30=0.45

通过一个充分细化的联合概率表来计算条件概率比较容易。举个例子来说，我们观测到一个学生是女生。给定学生为女生，则X的概率将要如何变化？我们需要计算条件概率P（X|Y=女生）。由式（8-5）得

图8-12形象地说明了这个两节点的贝叶斯网络。图中性别节点用黑体字标出以表明它已经被实例化——也就是说，已观测到的证据说明这个学生是女生。因此基于这个观察资料，X的概率就可以相应的更新。

在条件概率的计算中联合概率使用的一个问题就是，联合概率分布的充分细化需要大量的数据。对于一个两节点实例，需要相关的数据较少，因为只有2×3=6个联合概率。然而，一般说来，假设一个节点有n_i个离散值，则需要指定n₁n_2...nk条概率。对于有k个节点的贝叶斯网络而言，这个数字将大的不可想象。例如，对于一个有12个节点的贝叶斯网络，且每个结点都是二进制的（比如是/否），则需要指定2¹²=4096条联合概率（实际上，对于所有可能的组合而言，并不是所有联合概率都是有用的，因此即便对于最严谨的人而言，这种方法也会立刻陷入停顿）。

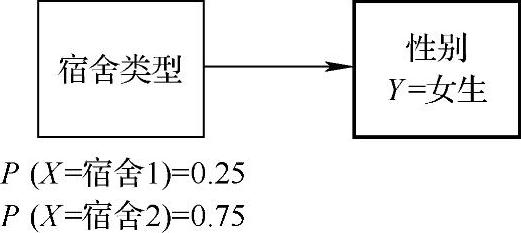
图8-12 性别节点实例化的两节点贝叶斯网络

幸运的是，贝叶斯网络的构建可以保持某些独立的假设（两个独立节点之间，其中一个事件的发生与否与另一个节点没有任何关系或影响^[6]）。后文中我们将进一步介绍关于贝叶斯网络中节点的独立性问题。现在，我们注意到这些独立的假设将使所需网络变量中指定概率分布的概率数目极大减少^[11]。

为了指定贝叶斯网络的概率分布，需要提供两种类型的概率：（1）根节点的先验概率（即无前驱节点）；（2）由母节点所有组合给定的非根节点的条件概率。接下来我们看一个具体的例子。图8-13所示为我们先前描述过的贝叶斯网络。

这里有两个根节点：机械故障和恶劣天气，图中给出了它们的先验概率。所谓先验概率，指的是不给出任何证据的前提下，一个事件发生的概率。图中给定的机械故障发生的先验概率是P（M1）=0.1，而恶劣天气发生的先验概率是P（B1）=0.2。

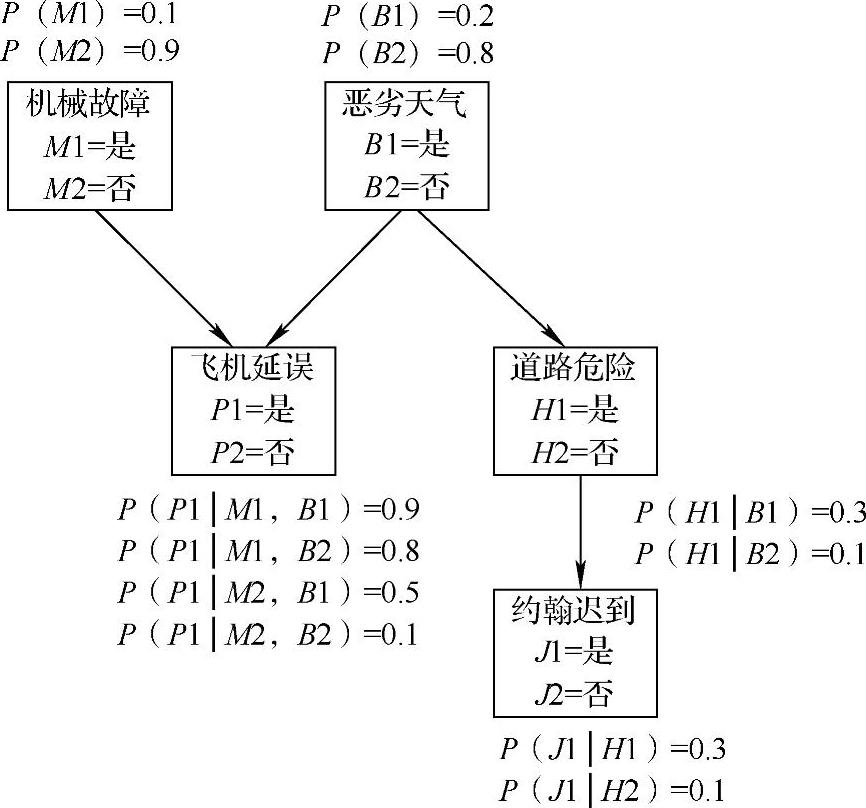
图8-13 指定了全部初始概率的贝叶斯网络

另外，图8-13中包括了给定母节点所有可能的组合情况下，全部非根节点的条件概率。例如，对于节点飞机延误来说，需考虑其母节点机械故障和恶劣天气的所有组合。因此其条件概率P（P1|M1，B1）、P（P1|M1，B2）、P（P1|M2，B1）和P（P1|M2，B2）均需要指定。因为由式（8-3）可以推算出P（M2）=1-P（M1），所以我们不必指定事件M2的条件概率。

从哪里得到这些先验概率和条件概率呢？幸运的话，可以根据历史数据得出。例如，可能有资料记录表明飞机有10%的概率会经历机械故障，同样从气象资料中可以查出恶劣天气的先验概率为20%（为了使系统更有规律，我们需要校正概率以反映一年的情况，举例来说，我们预计冬天出现恶劣天气的可能性要远高于夏天）。

条件概率的确定则是非常困难的。比如，假设同时出现了机械故障和恶劣天气，这时飞机延误的概率为P（P1|M1，B1）。这一数据可以从历史记录中得出，但是如果这些数据并不可用，或者非常难以获取，此时我们就需要根据专家观点来寻求其主观概率。贝叶斯方法的优点之一，就是可以同时使用历史数据和主观概率来决定先验概率和条件概率。当然，由于客观概率不经由人类专家观点中的偏差和可能的矛盾情况，因此更为可取。

结果对于5个二进制节点的贝叶斯网络来说，仅仅需要规定10个概率（2个先验概率和8个条件概率）。完整的联合概率分布却需要2⁵或者说是32个概率。对于更大的贝叶斯网络，这个数量的减少就会是极其显著的。实际上，贝叶斯网络的真正作用就是允许我们根据小得多的概率子集来推算出条件概率（接下来我们会看到一个例子，说明如何很快地计算条件概率）。这个显著地减少是由于贝叶斯网络的独立假设引起的，从而我们只需要考虑非根节点的母节点，或是上级节点即可。

通过使用条件概率及其母节点的先验概率信息，我们可以计算所有非根节点的先验概率。举例来说，飞机延误的先验概率可以通过如下方程计算：

P（P1）=P（P1|M1，B1）P（B1）+P（P1|M1，B2）P（M1）P（B2）+P（P1|M2，B1）P（M2）P（B1）+P（P1|M2，B2）P（M2）P（B2） （8-11）

因此在本例中的先验概率为

P（P1）=（0.9×0.1×0.2）+（0.8×0.1×0.8）+（0.5×0.9×0.2）+（0.1×0.9×0.8）=0.244

在没有给定其他任何条件的情况下，通过计算我们得出飞机发生延误的可能性为0.244。

同样地，道路危险的先验概率也可以通过公式计算，即

P（H1）=P（H1|B1）P（B1）+P（H1|B2）P（B2）=（0.3×0.2）+（0.1×0.8）=0.14

最后，根据公式来计算约翰迟到的概率：

P（J1）=P（J1|H1）P（H1）+P（J1|H2）P（H2）=（0.5×0.14）+（0.1×0.86）=0.156(www.daowen.com)

注意到P（H1），即H1的先验概率为0.14，可以求得P（H2）=1-0.14=0.86。

现在我们已经计算了所有非根节点的先验概率，如图8-14所示。我们现在将要介绍贝叶斯网络中最有趣的方面，即处理新近出现的证据，以及相应更新节点概率的能力。首先我们假设我们已经发现有道路危险的情况（即P（H1）=1.0）。图8-14b显示了作为这个新信息的反应节点概率如何变化。

首先，我们预计约翰迟到的概率将会增大。由于P（J1|H1）=0.3，P（J1）从0.156增大到0.3。我们同样预计天气恶劣的概率将会增加，因为我们注意到道路危险必然出现。因此我们需要计算P（B1|H1）。由式（8-6）我们求得

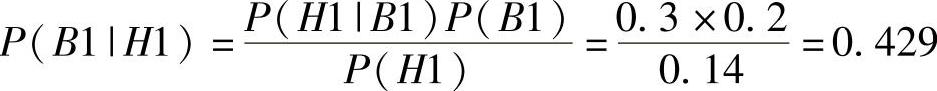
所以在已知发生道路危险的情况下，P（B1）将从0.2增加到0.429。如果天气恶劣的概率增加，那么我们同样会预计飞机延误的概率增加。我们先前由式（8-3）求得P（P1）。将P（B1）=0.429和P（B2）=1-0.429=0.571代入式（8-11）可得到以下结果：

P（P1）=（0.9×0.1×0.429）+（0.8×0.1×0.571）+（0.5×0.9×0.429）+（0.1×0.9×0.571）=0.329

P（P1）从0.244增加到0.329。我们认为节点机械故障不受道路危险的影响，因此其概率不变。图8-14b中给出了相应的计算结果，其中节点道路危险用黑体表示，用来说明此结点上的证据已经被观测到——也就是，节点情况一定发生。根据道路危险发生的证据，一个新的计算概率，也叫做后验概率，用来反映已知某一事件发生之后所计算出的条件概率。贝叶斯网络允许考虑逐渐增加的证据，即新的观测结果以及新证据将可能逐一出现，同时它们对贝叶斯网络的影响也将即时更新。继续我们先前的例子，我们进一步假定，可能在稍后的时间点，发现飞机的确是延误了。图8-14为更新了的贝叶斯网络。

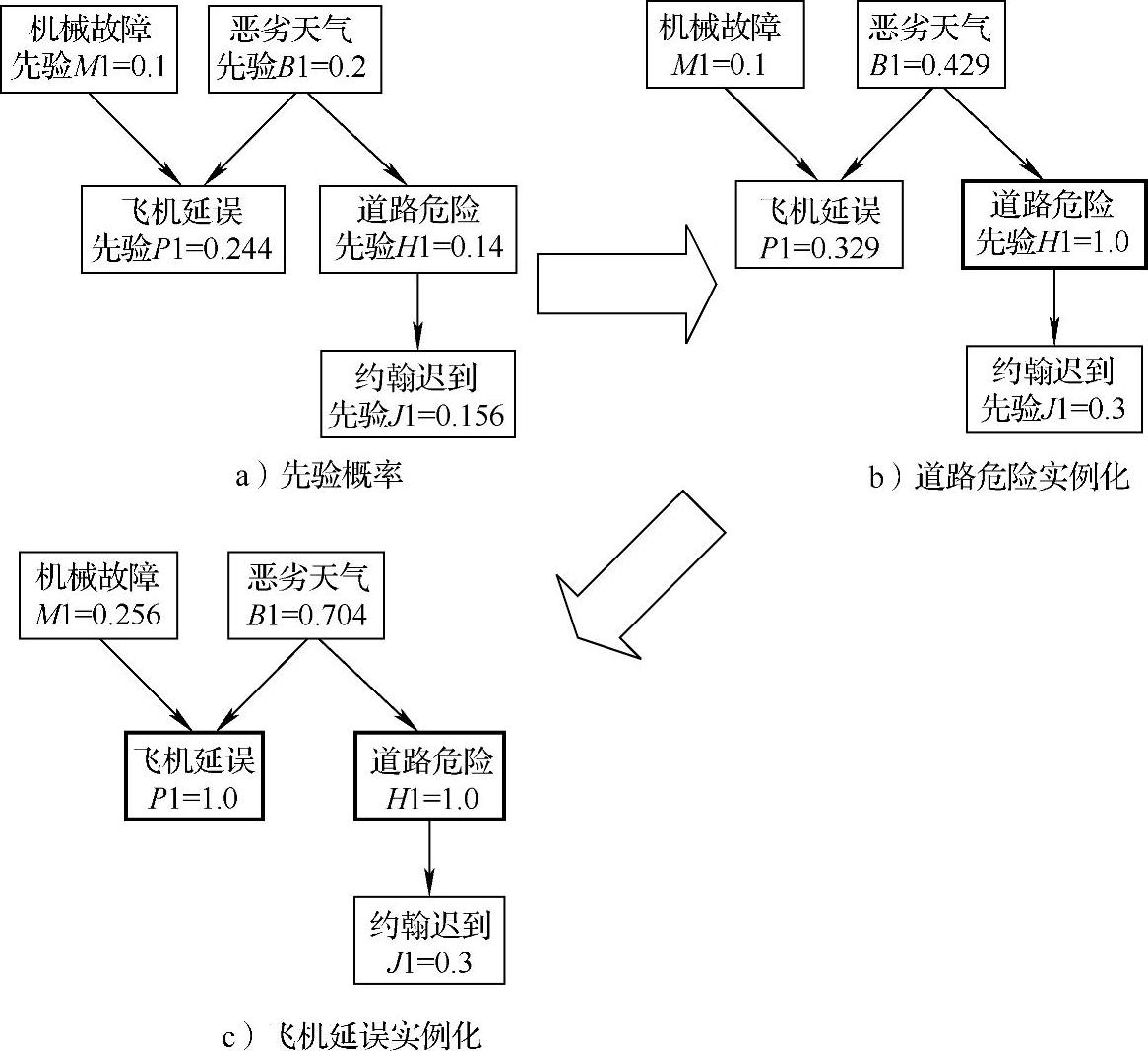
图8-14 更新了的贝叶斯网络

节点飞机延误的发生将会影响另外两个节点：机械故障和天气恶劣。我们预计新证据的出现，这两条概率均会增加。首先考虑P（M1|P1），或者是在飞机延误发生的前提下出现机械故障的概率。由式（8-6）可以知道：

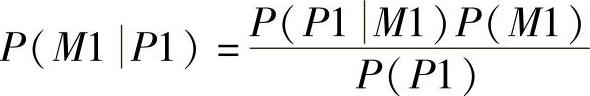
已知P（M1）=0.1，P（P1）=0.329，P（P1|M1）是多少？为了计算此概率，我们首先观测我们最初规定的P（P1|M1，B1），P（P1|M1，B2），P（P1|M2，B1），P（P1|M2，B2），或者是给定其母节点的所有组合时P1的条件概率。我们假定出现M1情况，因此无需考虑P（P1|M2，B1）和P（P1|M2，B2）两个条件概率。先前已知P（P1|M1，B1）=0.9，P（P1|M1，B2）=0.8，因此我们用下列方程进行计算：

P（P1M1）=P（P1M1，B1）P（B1）+P（P1M1，B2）P（B2）=0.9×0.429+0.8×0.571=0.843

代入先前的式中，有

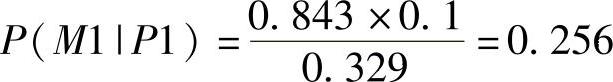
在已知飞机延误的前提下，机械故障发生的概率P（M1）从0.1增加到了0.256。

同样地，由式（8-6）计算P（B1|P1）：

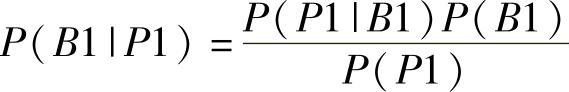
我们已知P（B1）=0.429，P（P1）=0.329，与计算P（P1|M1）相似，利用式（8-12）来计算概率P（P1|B1）：

P（P1|B1）=P（P1|M1，B1）P（M1）+P（P1|M2，B1）P（M2）=（0.9×0.1）+（0.5×0.9）=0.54

将这些数据代入得到最后的结果：

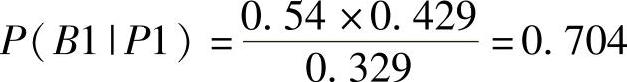
正如我们所预期的，天气恶劣的概率也从0.429增加到了0.704。

这个例子说明了在贝叶斯网络中因果关系的结构如何用来传播概率。因此贝叶斯网络的一个明显的特征就是它具有推断问题结构和传播概率的能力。在这方面，贝叶斯网络的确是一种基于模型推理的类型（详见第7章）。由于系统行为由系统结构决定，因此贝叶斯网络是一种问题的解决通过系统结构知识支持的推理类型。为了使这些想法更加精确具体，我们来考虑贝叶斯网络中各种可能的结构，参见图8-15给出了三种类型。

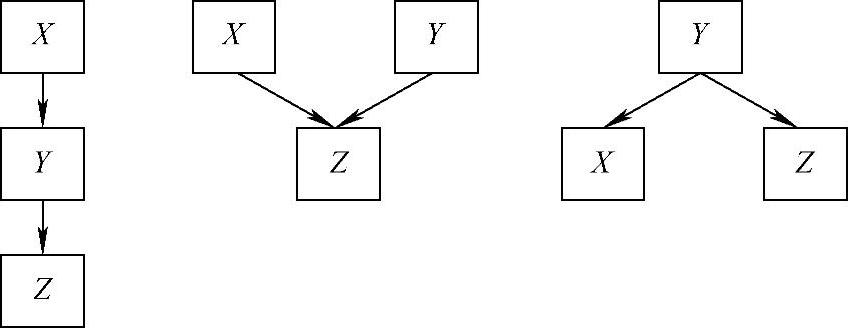
图8-15 贝叶斯网络的三种连接类型

在线性结构中，三个变量x，y，z呈因果链接关系，即x导致y，y导致z。如果有x出现的证据，则可以传递给y，进而传递给z。在图8-14给定的贝叶斯网络中，就是一个线性结构。天气恶劣的证据将会增加道路危险的可能性，进而增加约翰迟到的可能性。

现在，我们假设Y一定发生（在这种情况下，我们确信会出现道路危险的情况）。如果真是这样，那么X的信息对Z没有任何影响（事实上，Y的实例化，会阻碍或忽略从X到Z信息的传递）。实际上，在本例中（见图8-14c），当天气恶劣的证据增加时，约翰迟到的概率保持不变，这是由于已知道路危险的情况一定发生。这种情况下，给定Y（道路危险）时X（天气恶劣）与Z（约翰迟到）是相互独立的。

下面给出一种普遍情况。若一个贝叶斯网络由n个节点呈线性结构连接，其中节点N_k实例化（k<n），则从N₁到N_k-1的节点信息对从N_k+1到N_n的节点没有任何影响（见图8-16）。

图8-16 节点N_k实例化的线性机构网络

第二种类型的连接方式为聚集结构，即两个原因（X和Z）聚集到一个单一的结果（Y）。显而易见，不管X单独发生，或者Z单独发生，或者两者同时发生都会影响Y。另外，若有X和Z同时发生，则Y发生的可能性比单独X或单独Z发生时要大。进一步说，若有Y发生，也会影响原因X和Z。图8-14给出了一个聚集结构的例子，其中机械故障和天气恶劣两个节点都会导致飞机延误（注意到在我们的例子中，我们已经证明了飞机延误的实际发生会逆向同时增加机械故障和天气恶劣的概率）。

从X到Z的信息传输会如何变化？若我们没有任何Y的证据，则X和Z相互独立（在例子中，若我们没有飞机延误的证据，则机械故障和天气恶劣相互独立）。因此，当Y的证据没有给定时，X的证据不会传递给Z，反之亦然。但是，如果有一些关于Y的信息，则X和Z将会相互关联。例如，假设我们已知飞机发生延误，进一步假设我们也有机械故障的证据。那么我们预计天气恶劣的概率将会降低，因为我们推断飞机延误是由机械故障导致的，而非天气恶劣。用这种方法，我们已经通过解释消除天气恶劣是一种原因。另一方面，若我们有飞机延误的证据，同时我们已知机械故障的概率降低，那么类似地，我们可以预计天气恶劣的概率会增加。

第三种类型的连接方式为发散结构，即两个结果X和Z有一个共同的原因Y。无疑，任何Y的证据都会同时传递给X和Z。一个更有意义的问题就是从X到Z之间是否有证据的传递？若Y并没有实例化（即我们不确定Y是否发生），那么证据的确可以从X到Z传递。我们可以通过图8-14观察到这种情况，其中天气恶劣是导致飞机延误以及道路危险的共同因素。当我们将道路危险实例化时，就会影响到天气恶劣的概率更新，进而增加飞机延误的可能性。因此，当Y不确定时，X和Z之间并非相互独立。相反地，假设将Y实例化，则X的证据不会对Z起任何作用，反之亦然。例如，我们假定天气恶劣一定发生，那么飞机延误的证据将不会传递到道路危险，同样道路危险的证据也不会传递到飞机延误。在类似线性结构的贝叶斯网络中，实例化的节点阻碍证据到其他节点间的传递。

从某种意义上讲，不确定性的因果（影响）关系和传播已经被数学化，因此使得基于概率论原理和贝叶斯理论的概率是一致且正确的。因此无论采用什么方法，必须根据先前标注的结构元素如线性连接、聚集连接和发散连接，来计算和更新某些概率。这就是贝叶斯网络中最卓越的成就：使用数学算法，使得因果图上的概率可以适当的传播。

在第1章中，我们描述并定义了一个智能用户接口的解释功效，同时指明提高解释功效的两种优点：透明性，即了解系统如何工作的能力；灵活性，即接口可以适应于各种各样终端用户交互的能力。可以这样说，贝叶斯网络在这两方面都非常出众。首先，贝叶斯网络是高度直觉和图形化的，这使我们可以以网络图的形式建立因果关系的模型。由于贝叶斯网络的图形化，我们可以很容易地观察到新证据对因果图中节点的影响。因此在推理过程中可以考虑到高度的透明。其次，贝叶斯网络具有高度的灵活性，新证据可以以任意顺序插入（即任何位置的节点都可以实例化），同时贝叶斯网络会随之更新。另外，贝叶斯网络可以基于不完整的证据来做出预测，因此具有较强的鲁棒性，不会因为某些不可获得的证据而完全破坏整个网络。贝叶斯网络不仅可以从因到果进行推理，从果到因也可以，因此贝叶斯网络可以进行逆向推理，这在包括置信度方法在内的其他方法中都是不可能的。

贝叶斯网络的另一个优点是它是一种表示专家主观判断的绝佳方法。正如我们早先提到的，贝叶斯网络中最初指定的先验概率和条件概率可以表示主观专家意见或客观数据信息。贝叶斯网络将会同等的处理两种类型的信息。相反地，其他统计方法，诸如回归分析法，依靠的是高度的数据驱动，而忽略考虑专家意见。基于这个原因，回归模型局限于对过去的描述，而对预测未来则很少成功。贝叶斯网络包含了专家意见和因果解释，因此更适合于需要预测未来事件的情况^[12]。