条件概率是指一个事件的概率会在已知另一事件发生的情况下发生变化。一般记作P（A|B），读作“在B条件上发生A的概率”。计算任意两个事件A和B的概率，我们可以使用如下公式：

式中，P（B）＞0。

通过图8-9可以更好地理解上述公式。若我们已知事件B发生，然后计算事件A发生的概率，我们仅需求取事件AB和事件B的概率比值。

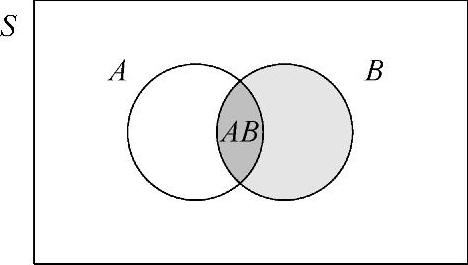
图8-9 P（A|B）为事件AB和事件B的比值

例：假设我们掷两个骰子，我们想求它们和大于等于11的概率。我们将掷出两个骰子的样本空间S表示为包含36种可能结果的集合：

（1，1）（1，2）（1，3）（1，4）（1，5）（1，6）

（2，1）（2，2）（2，3）（2，4）（2，5）（2，6）

（3，1）（3，2）（3，3）（3，4）（3，5）（3，6）

（4，1）（4，2）（4，3）（4，4）（4，5）（4，6）

（5，1）（5，2）（5，3）（5，4）（5，5）（5，6）

（6，1）（6，2）（6，3）（6，4）（6，5）（6，6）

若事件A表示两个骰子之和大于等于11的概率，则为了计算P（A），我们首先注意到A事件发生有三个可能结果：A={（5，6），（6，5），（6，6）}。因此，由式（8-1）得

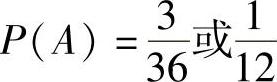
进一步假设，我们已经事先观察到事件B为第一个骰子投出的是6，则事件A在事件B发生下的概率如何变化？

直觉告诉我们这种情况下此概率会增加。为了验证我们的直觉，我们需要计算事件B为第一个骰子为6情况下的P（A|B）。

由式（8-5），我们需要计算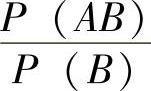。如果AB表示两个骰子之和大于等于11且第一个骰子为6，即AB={（6，5），（6，6）}，同时B={（6，1），（6，2），（6，3），（6，4），（6，5），（6，6）}。则

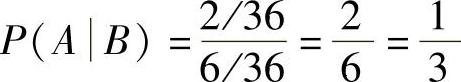
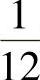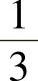根据我们的预测可以看出，在第一个骰子为6的前提下，概率从增加到。我们现在由式（8-5）得出贝叶斯定理：

1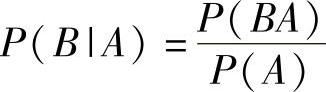），将式（8-5）中的A和B换位；

2）P（BA）=P（B|A）P（A），移项重新整理；

3）P（AB）=P（B|A）P（A），根据联合概率的交换性，有P（BA）=P（AB）；

4）P（A|B）P（B）=P（B|A）P（A），式8-5中的P（AB）由P（A|B）×P（B）代替；5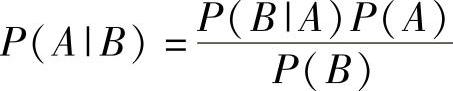），两边同除以P（B）。上述最后一个方程就是贝叶斯定理的简化形式。可以描述如下：

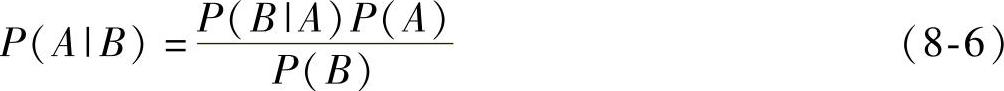
式中，P（B）＞0。

1.疾病检测试验

假定有一项疾病检测试验的准确率为95%。换句话说，当对病人执行某一种疾病的检测试验时，若病人确实患有此种疾病，则95%的测试可以得到对疾病阳性的结论（其余5%得到一个假阴性的结论）。同样的，若病人确实没有患此种疾病，则95%的测试可以得到对疾病阴性的结论（其余5%得到一个假阳性的结论）。进一步假设疾病在人群中的流行程度为1/1000，那么一个人经测试患病同时确实患病的概率是多大？

我们可以把这个问题规划成条件概率并利用式（8-6）（贝叶斯定理）。令A为一个人患有此种疾病的事件，B为一个人疾病检测试验为阳性结论的事件。因此我们需要解决并且计算P（A|B）。首先我们知道，给定了P（B|A）=0.95。其次我们也知道P（A）=1/1000（人群中此种疾病的流行程度）。

但是P（B）是多少？为了计算P（B），需要使用下述方程：

P（B）=P（B|A）P（A）+P（B|┐A）P（┐A）（8-7）

P（B）的计算需要将事件B分割为两个互斥的穷举事件：人患有此病（事件A）和人不患此病（事件非A）。（后文中我们将进一步介绍分割样本空间的内容）。将式（8-7）代入式（8-6）可以得到贝叶斯定理一个非常有用的形式：(www.daowen.com)

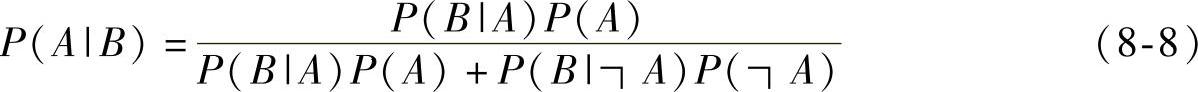
为了求解方程，我们需要P（B|┐A）和P（┐A）。P（B|┐A）指的是一个人没有患病却测试为阳性的概率，即1-0.95或0.05。P（┐A）指的是一个人没有患病的概率，即1-1/1000，也就是999/1000。将这些值代入式（8-8）中可以得到下列算式：

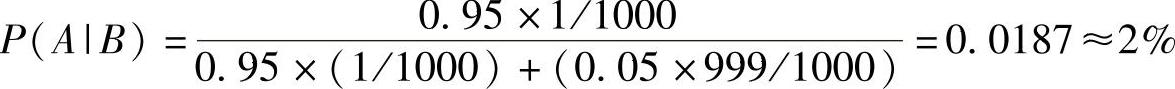
因此，当疾病检测为阳性时，一个人确实患病的概率大约为2%。对于那些期望可靠的测试（95%准确率）能带来更高精确判定的人来说，这个结果让人大吃一惊（事实上，作为一个知名的研究，这个问题曾向哈佛医学院的学生和教职员提出，超过半数的人认为如果疾病测试为阳性的话，有95%的概率确认患有疾病）。但事实与直觉不同，对于测试为阳性的人而言，仅仅有2%的人确实患病。事实上，在决策科学文献中，通常将这一类个人偏见称作“基率缪误”。它指的是人们在处理解决这些概率问题时，仅仅依靠直觉而忽视基本数据情况的现象。在这个例子中，人群中患病的基本概率非常低（仅有1/1000）。

2.贝叶斯定理通式

贝叶斯定理通式需要对样本空间分割的理解。如图8-10所示，样本空间S被分割成k个事件A₁，A₂，…，A_k，并且它们为互斥穷举事件（即各个事件互不交叉且其并集为全集A₁∪A₂∪…∪A_k=S）。并且，事件A₁B，A₂B，…，A_kB组成事件B的一个分割，如下：

B=（A₁B）∪（A₂B）∪…∪（A_kB）

此外，由于A₁B，A₂B，…，A_kB为互斥事件，根据公理3，可以写出：

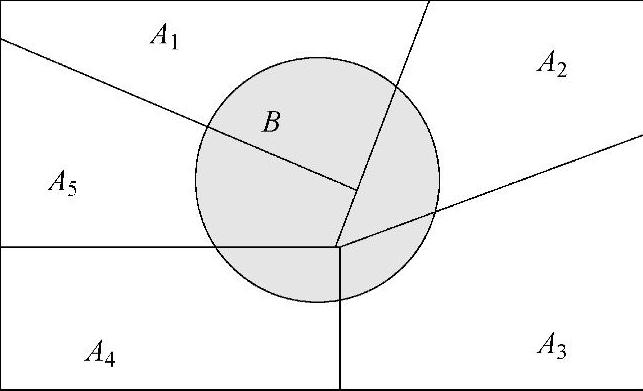
图8-10将样本空间S分割为A₁～A₅

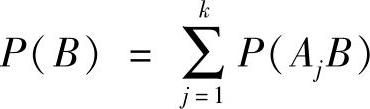
最后，由式（8-5）P（A_jB）=P（A_j）P（B|A_j）可以得出：

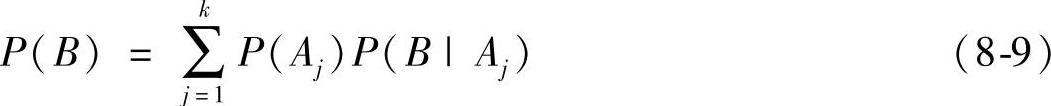
下面我们就将给出贝叶斯定理的通式：

假设k个事件A₁，A₂，…，A_k构成了样本空间S上的一个分割（它们均为S上的互斥穷举事件），则对于所有i都有P（A_i）>0，且令B为任意事件，有P（B）>0。那么对于全部的i=1，…，k，有：

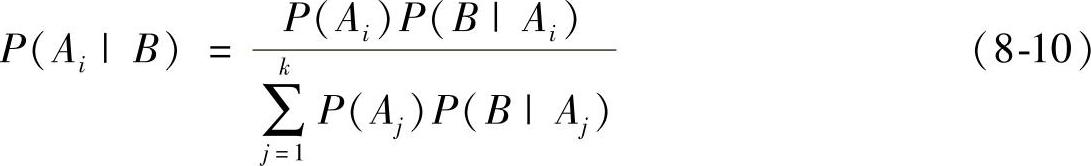
证明：由式（8-5）得

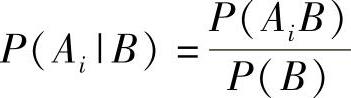
式（8-10）中右边的分子等于P（A_iB），而分母等于式（8-9）的P（B）。

例：一个硬盘制造商销售三种型号的硬盘机：品牌1、品牌2和品牌3。经过一年的使用，这三种不同品牌的硬盘机出现了不同程度的损坏：品牌1的损坏率为20%，品牌2的损坏率为10%，品牌3的损坏率为5%。制造商对于三种品牌的生产份额分别为：品牌1为30%，品牌2为50%，品牌3为20%。

假设从这一批生产的硬盘机中随机挑选一个，使其精确运行整一年时间。一年后发现这个硬盘机损坏了。那么这个硬盘机是品牌1的概率为多少？是品牌2的概率为多少？是品牌3的概率又为多少？

令A_i是选中品牌i的事件，这里i=1，2，3。且令B为硬盘机运行一年后损坏的事件。我们需要计算条件概率P（A_i|B），由贝叶斯定理式（8-10）得：

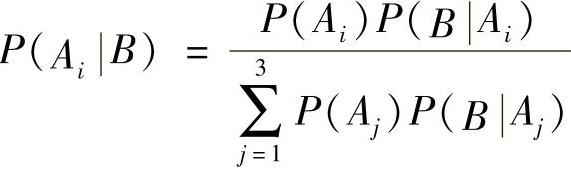
根据前文我们已知下列概率：

品牌1：P（A₁）=0.3 P（B|A₁）=0.2

品牌2：P（A₂）=0.5 P（B|A₂）=0.1

品牌3：P（A₃）=0.2 P（B|A₃）=0.05

因此相关的计算如下：

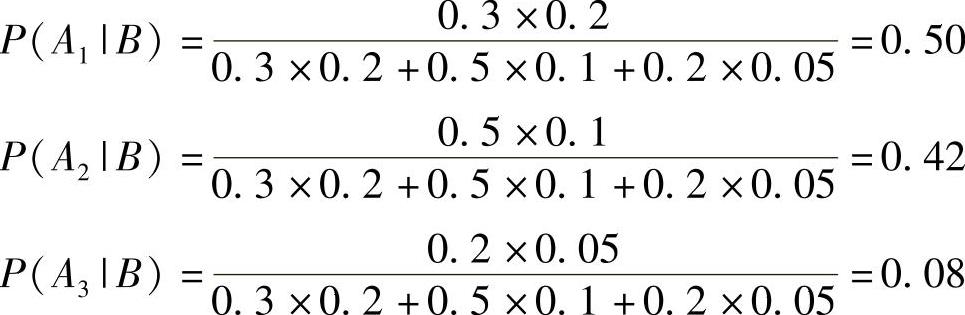
注意因为事件A₁、A₂、A₃构成了S上的一个分割，并且它们为互斥穷举事件，因此可以使用贝叶斯定理的通式式（8-10）。