当做某类实验时,将概率看做是结果出现的可能性是很有用的。在概率论中,实验这个术语用来指代任何“事先不能确切知道结果的过程[8]”。例如:
•在一个投掷硬币的实验中,实验者想要知道10次投掷中出现6次及6次以上正面的概率。
•从洗好的52张纸牌中选取两张,实验者想确定出现21点的概率(21点是指选择的两张牌之和为21:包括一张Ace牌和一张10点以上的牌)。
•两个盒子中含有不同数量的红球。第一个盒子中,10个球中有8个红球(80%红球);第二个盒子中,10个球中有2个红球(20%红球)。实验者想要确定若从两个盒子中选择一个红球,而这个红球是从第一个盒子中选出来的概率。
在上述三个例子中,传统意义上是不需要实际做实验的。实际上,概率论的优点和影响力就是:这些概率可以通过计算得出,而不需要设计实际的实验。
实验的所有可能结果组成了样本空间,我们将其表示为S。样本空间是包含所有可能结果的集合,而其中每一种结果都是集合中的元素。因为这种约定,集合论的语言和概念为理解概率论提供了一个良好的构架。
举个例子,当我们投掷骰子的时候,我们可以将样本空间表示为S={1,2,3,4,5,6}。我们将这种每条结果出现的概率相等的样本空间称作简单样本空间。进一步的,将A为定义在S子集的任意事件,表示为A⊆S。事件发生的概率用P(A)表示。例如,在投掷骰子的实验中,若A表示投出的数字为偶数的事件,则A={2,4,6}。假定事件A包含m个结果,样本空间包含n个结果,那么

即
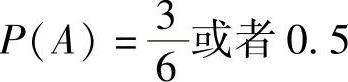
例:假设投掷三次硬币,计算下述概率:(1)有且只有两次为正面向上;(2)至少有两次正面向上。
我们将此实验的样本空间表示为如下形式:
S={正正正,反正正,正反正,正正反,反反正,反正反,正反反,反反反}
若事件A表示有且只有两次正面向上,则A={反正正,正反正,正正反}。A中有三个等概率的元素,而S中有8个等概率的元素;因此,
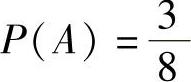
依此类推,若B表示至少两次为正面向上的概率,则B={正正正,反正正,正反正,正正反}。同样,有
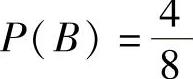
为了满足全部概率的描述,数学家在形式上精确地给出了三条公理来定义概率。第一条公理表明概率总是非负的。
公理1: 对于任意事件A,P(A)≥0
第二条公理表明若一事件确定会发生,则其概率一定为1.
公理2:P(S)=1
公理1和公理2联合,可以得到下列结果:
0≤P(A)≤1(8-2)
式(8-2)精确的定义了概率的范围是实数从0~1。不可能发生的事件概率为0,必然发生的事件概率为1。所有这两种极端情况间的概率表示了结果相对的不确定性程度。
在介绍公理3之前,我们首先讨论三种集合运算,以帮助了解概率的计算。正如我们先前提到的,集合论的语言规则可以便于描述概率。第一种集合运算是并集(union):对于任意的两个事件A和B,其并集定义为包含只属于A,只属于B,或者同时属于A和B的结果的事件,并集用符号表示为A∪B。第二种集合运算是交集(intersection),A和B的交集定义为包含同时属于A和B的所有结果的事件。交集用符号表示为A∩B,或者简写为AB。第三种集合运算称为补集(comple-ment),事件A的补集指样本空间中不属于A的结果的集合。有时补集可以描述为“非A”,用符号表示为┐A。图8-8给出了这三种集合运算的韦氏图。(https://www.daowen.com)
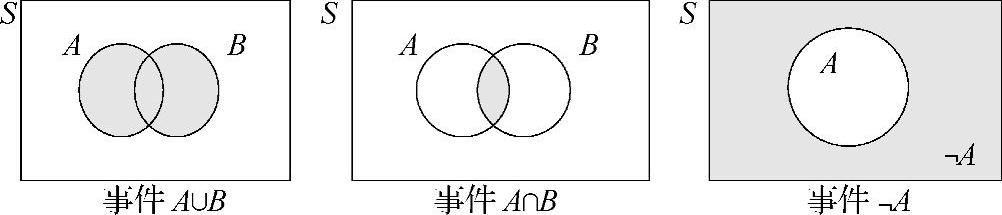
图8-8 集合运算
例:从标准的52张扑克牌[4]中随机抽出一张,则样本空间S包含了52种可能的结果。进一步考虑如下三个事件:
1)A表示抽出一张花牌(K、Q、J)的事件。
2)B表示抽出一张红心Q的事件。
3)C表示抽出一张2的事件。
上述三个事件相应的概率分别为: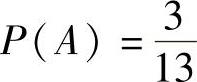 ,
,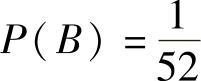 ,
,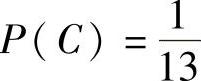 。我们还可以计算下列概率:
。我们还可以计算下列概率:

P(AC)=P(一张花牌AND一张2)=P(Ø)=0
为了计算一个事件补集的概率,我们可以简单地计算此事件的概率,然后被1减去而得到:
P(┐A)=1-P(A)(8-3)
例如,计算概率P(┐A)=P(抽到的不是花牌):
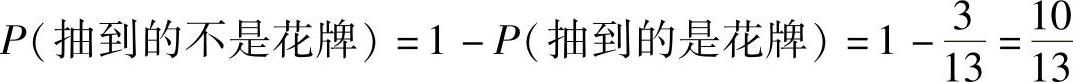
若事件A1和A2没有共同元素,我们就可以说事件A1和A2是互斥的,或者说不相交的,表示为A1A2=Ø。对于任意两个互斥事件A1和A2,总有
P(A1∪A2)=P(A1)+P(A2)
下面就k个互不相交事件的情况,我们将阐述公理3。
公理3:给定k个互斥事件A1,A2,A3,…,Ak,其中至少有一个事件发生的概率(即k事件发生的并集的概率)等于每一个事件单独概率之和,即P(A1∪A2∪A3…∪Ak)=∑ki=1P(Ai)
另一方面,当两个事件A1和A2并不互斥[5]时(即A1A2≠Ø),则我们计算其并集必须遵循下列方程:
P(A1∪A2)=P(A1)+P(A2)-P(A1A2) (8-4)
例:在上例中,由于事件A(抽到一张花牌)和事件C(抽到一张2)为互斥事件,所以当计算P(A∪C)时,可以通过P(A)+P(C)计算得出。因为绝不可能同时抽到一张花牌和一张2。另一方面,事件A(抽到一张花牌)和事件B(抽到一张红心Q)不是互斥事件,因为红心Q本身就是一张花牌。因此
P(A∪B)≠P(A)+P(B)由式(8-4),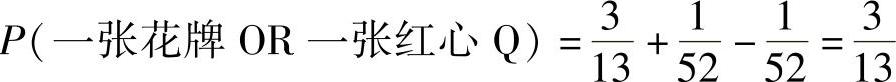 。
。
再举一个例子,假设A表示抽到一张花牌的事件,B表示抽到一张黑桃的事件。由式(8-4)以及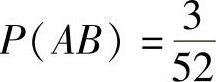 ,进而得到如下算式:
,进而得到如下算式:
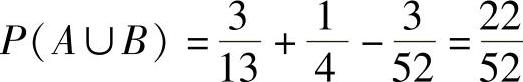
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







