由于置信度方法是两种方法中更容易理解的方法，因此我们首先介绍置信度。实际上，置信度是20世纪70年代由MYCIN的开发者提出来的。它作为一种便利的、无需精确的数学证明的方法，可以进行不确定数据和结论的处理^[3]。MYCIN曾在第5章中出现过，它是一个基于规则的专家系统，是用来诊断（并且提出治疗方案）细菌感染的。它允许如下形式的IF-THEN规则表示：

IF（条件₁的置信度为x₁AND条件₂的置信度为x_2...AND条件_n的置信度为x_n）

THEN（结论₁的置信度为y₁AND结论₂的置信度为y_2...AND结论_n的置信度为y_n）

在MYCIN中，条件用来表示证据，诸如实验室的试验结果和病人的症状；结论用来表示给定证据的前提（例如，病人的疾病）。x值代表的是证据为真的程度，其值域为（0，1）；y值代表从证据中所得结论的程度，在MYCIN中指定其值域为（-1，+1）。值1代表无论何时，只要满足全部条件，结论一定为真。而值-1则代表同样情况下结论一定为假。表8-1提供一种给一条规则分配值的方法，它是通过采访某一领域专家所获得的。举个例子来说，一位心脏病专家可能这样诊断：“我几乎确定（但不是100%确定），根据病人的胆固醇指数（同时包括高密度脂蛋白指数HDL和低密度脂蛋白指数LDL），同时考虑到病人的其他危险因素，通过使用降低胆固醇的药物治疗，可能会使病人病情好转。”基于这条信息，知识工程师将给建议降低胆固醇药物的规则分配置信度为+0.8。

表8-1 置信度表

一个专家系统如何在证据不确定或者数据混杂的情况下进行置信度的处理呢？以下是MYCIN^[4]中给出的一种（虚拟的）置信度规则：

IF（1）有机生物体呈革兰氏染色阴性（0.9）AND

（2）有机生物体呈杆状形态（0.7）AND

（3）有机生物体为需氧生物（0.4）

THEN有强烈（0.8）的证据说明这一类有机生物为肠杆菌科

一种惯例是无论何时涉及条件与（AND），都取其中置信度的最小值。例如在（0.9，0.7，0.4）中取最小值为0.4。我们之所以在条件与中取置信度的最小值，是因为从某种意义上说，我们条件与确定的是最弱的部分。这就相当于说一条锁链的紧固程度和其最弱连接处坚固程度是一样。

为了计算结论的全局可信度，考虑到各个逻辑前提的不确定性，我们将采取一种简单的计算方法：

CF（规则行为）=CF（前提）×CF（结论）

因此，据上述公式，我们可以计算出置信度：

CF（有机生物为肠杆菌科）=0.4×0.8=0.32

假设取代一系列条件与，规则采用条件或（OR）来编码，其原则如下：

IF（1）有机生物体呈革兰氏染色阴性（0.9）OR

（2）有机生物体呈杆状形态（0.7）OR

（3）有机生物体为需氧生物（0.4）

THEN有强烈（0.8）的证据说明这一类有机生物为肠杆菌科

这种情况下，我们将改用（0.9，0.7，0.4）中的最大值。因为通过条件或我们所确定的，在某种意义上来说是能确定的最强的部分。因此，对于规则或，置信度的计算方法如下：

CF（有机生物为肠杆菌科）=0.9×0.8=0.72

有时两条或者更多条的规则会影响同样的假设。那么当这种情况发生时，一个专家系统将如何确定其置信度呢？假设有这样一个例子，我们给定下列三条原则，它们全都影响假设H：

规则1：IF A AND B AND C

THEN H（CF 0.8）

规则2：IF D OR E(www.daowen.com)

THEN H（CF 0.9）

规则3：IF F

THEN H（CF-1.0）^[2]

如果观测到上述三条规则中所有证据，也就是观测到A、B、C、D、E和F置信度在不断地变化，我们如何确定置信度呢？为了计算涉及cf₁（由一条规则设立的置信度）和cf₂（由另一条规则设立的置信度）的联合置信度，我们可以使用下列方程之一来计算^[6]。

传播方程1.假设的可信度增加（cf₁＞0且cf₂＞0）

cf（cf₁，cf₂）=cf₁+cf₂（1-cf₁）

传播方程2.假设的不可信度增加（cf₁＜0且cf₂＜0）

cf（cf₁，cf₂）=cf₁+cf₂（1+cf₁）

传播方程3.矛盾结论（置信度符号相反）：

（cf₁＞0且cf₂＜0）或（cf₁＜0且cf₂＞0）

（cf₁＞0 and cf₂＜0）or（cf₁＜0 and cf₂＞0）

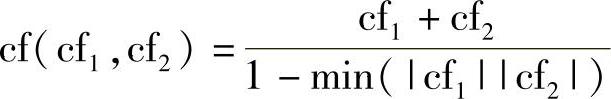
式中，|cf₁|和|cf₂|分别为cf₁和cf₂的绝对值。

我们假设首先观测到A（cf 0.8），B（cf 0.4）以及C（cf 0.6）。基于这条证据，执行规则1并计算cf（H）：

min（0.8，0.4，0.6）×0.8=0.4×0.8=0.32

接下来根据观察到的D（cf 0.8）和E（cf 0.9）。基于这条证据，执行规则2并计算cf值为：

max（0.8，0.9）×0.9=0.9×0.9=0.81

通过传播方程1（由于cf₁和cf₂都是正数），我们可计算联合置信度如下：

0.32+0.81×（1-0.32）=0.87

这个例子说明这两条规则会导致假设H的可信度增加，结果是置信度值为0.87。

最后，我们观察到F（cf0.6）时，执行规则3且计算cf值如下：

0.6×（-1.0）=-0.6

由于这是一个矛盾的结论（即cf₁和cf₂符号相反），我们可以根据传播方程3得到最终的置信度：

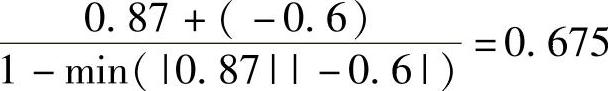
根据我们的预期，H的置信度已经降低（从0.87降低到0.675）。