为了阐述基于模型诊断的原理，让我们看一下一个简单的设备，其结构如图7-2所示。该设备包含10个部件：5个加法器（Add-1到Add-5）；2个加倍装置（Double-1和Double-2），两个乘法器（Multiply-1和Multiply-2），和一个二次方器（Square-1）。该设备结构给出了部件之间是如何相互连接的，并且连接是有方向的。如图中箭头所示，表明它们作为输入通向一个部件或者作为输出从一个部件导出。注意在图中两根导线的交叉或者是相连的或者是不连的，图7-3阐述了用于区分相连导线和不相连导线之间的标记法。相连导线在线的交叉处用一个色点来表示；不相连导线用桥式符号表示以说明有两根导线，但它们不相连。

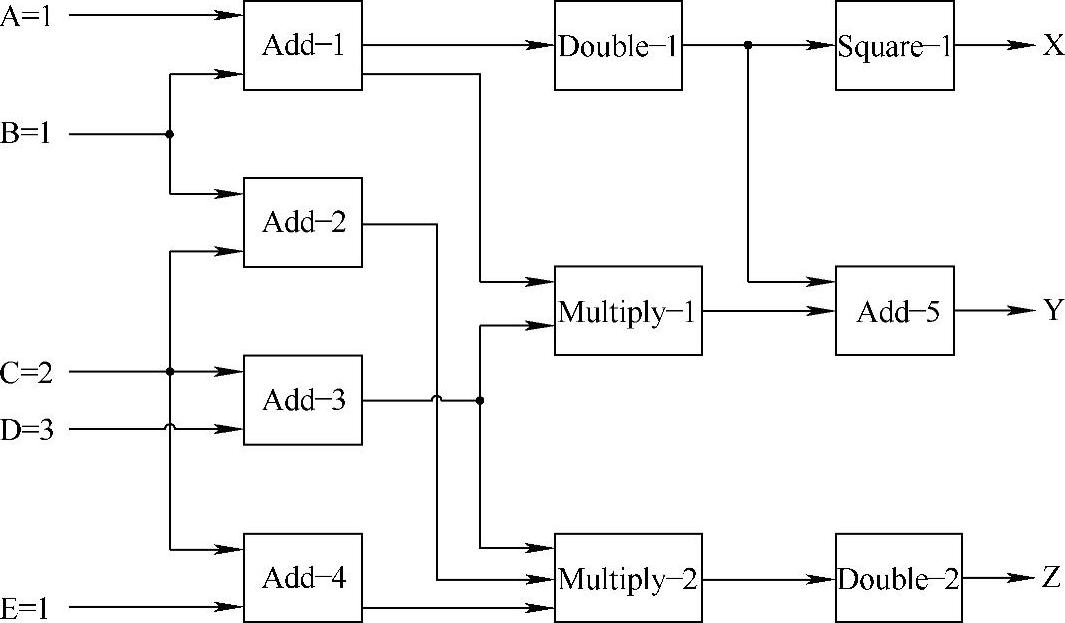
图7-2 一个简单设备的拓扑结构

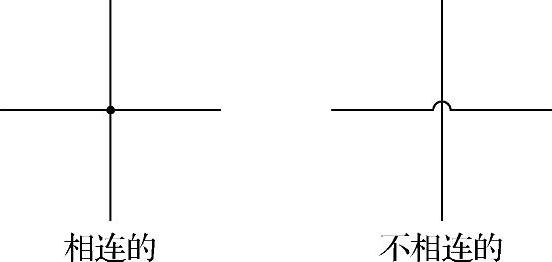
图7-3 交叉的相连和不相连导线的标记法

除设备结构外，我们也需要部件行为的一个描述。行为可以通过指出进入一个部件的输入如何转变成输出的数学表达式或方程来表达。图7-2中的部件将完成下列工作：输入相加（部件Add-1到Add-5），输入相乘（部件Multiply-1和Multiply-2）输入加倍（部件Double-1），或者输入二次方（部件Square-1）。

图7-2也表明设备包含5个输入，以A到E标注，和三个可观测的输出为X，和Z。

让我们假定我们已经检测到有差异（图7-4为表示这种情况的图形）。此图表明当我们运行设备模型时，我们预测Y=14，但我们观测到的Y=9。

我们在基于模型诊断中的第一步就是去辨识哪个部件能解释设备差异行为的原因。我们称第一步假设产生，因为我们基于设备的结构和行为，正在假定哪个部件解释差异的原因。我们定义一个推测作为被除数辨识出来作为差异可能原因的部件。我们的目标就是消除或免除尽可能多的推测，以便仅有几个剩下，或是最好的情况，只有一个推测剩下。为了做到这点，可以利用许多规则去辨识和限制推测集。

规则1

一个推测必须与差异联系。

基于设备拓扑，只有部件与差异相连时，它才能被牵连进来。在图7-4中，所有10个部件都与在Y处出现的差异相关联，因此在这种情况下，规则没有从推测集中消除任何部件。

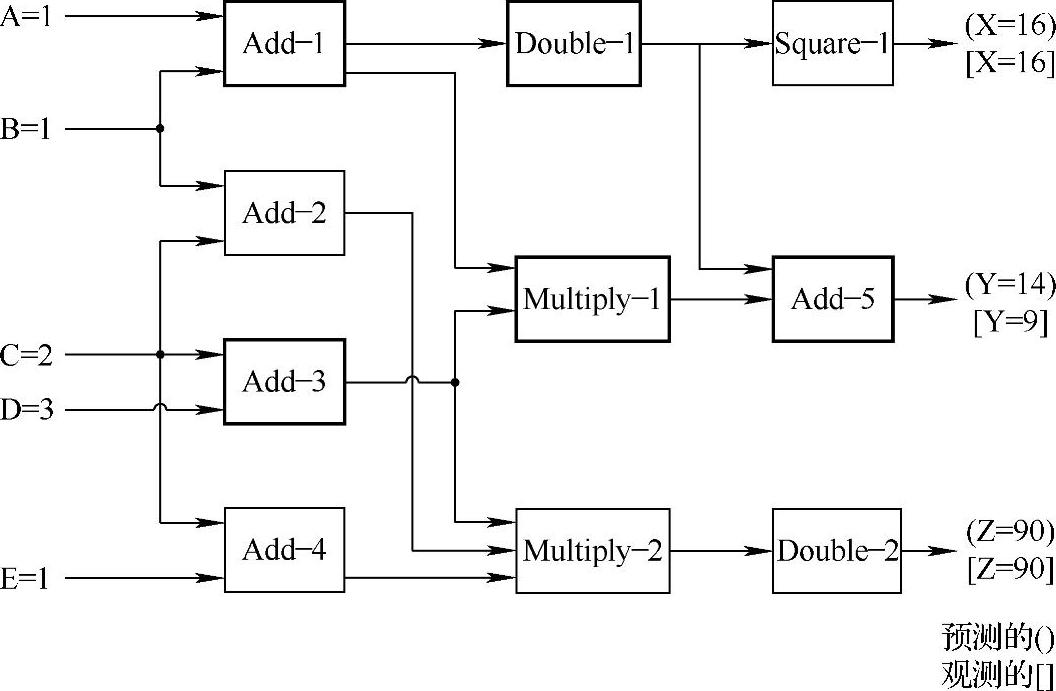
图7-4 Y处能观测的故障

规则2

从误差中向上游得到的必然推测。

我们用向上游意味着什么？上游的部件指的是与差异输入侧相连接的部件。为了辨识哪些部件是顺势的，我们需要带有定向连接的设备拓扑，并用箭头指出一个部件的输入和输出。从图7-4中的差异Y中可以向上游得到5个部件：Add-1，Add-3，Double-1，Multiply-1和Add-5（图中这5个部件都用黑体标出）。因此规则2从推测集中除去了5个其他的部件。

规则3

如果推测是由一致性的输出得到，我们可以免除推测，但是我们必须注意如果涉及故障屏蔽则不能免除。

当预测值与观测值相同时输也是一致的。因此X和Z是一致的输出。由规则3，由于Add-1和Double-1都是由X得到，Add-3由Z得到，因此可以免除。故我们只剩下两个推测，Multiply-1和Add-5。

不幸的是，如果涉及故障屏蔽，规则3可以导致一个貌似真实的推测免除。当一个设备接收到错误的输入从而产生一个一致的输出时，故障屏蔽就会出现。图7-5就是一个故障屏蔽如何出现的示例。输出Z的预测值和观测值都是90，所以是一致的。然而，两个上面的部件（Add-2和Add-4）是有误差的，以致不正确的输入被读入Multiply-2。尽管这样，在Multiply-2和Z处还是产生了一致的输出。可能还需要部件的进一步检验以确定故障屏蔽没有发生（后面在假设检验部分我们会讨论这个）。(www.daowen.com)

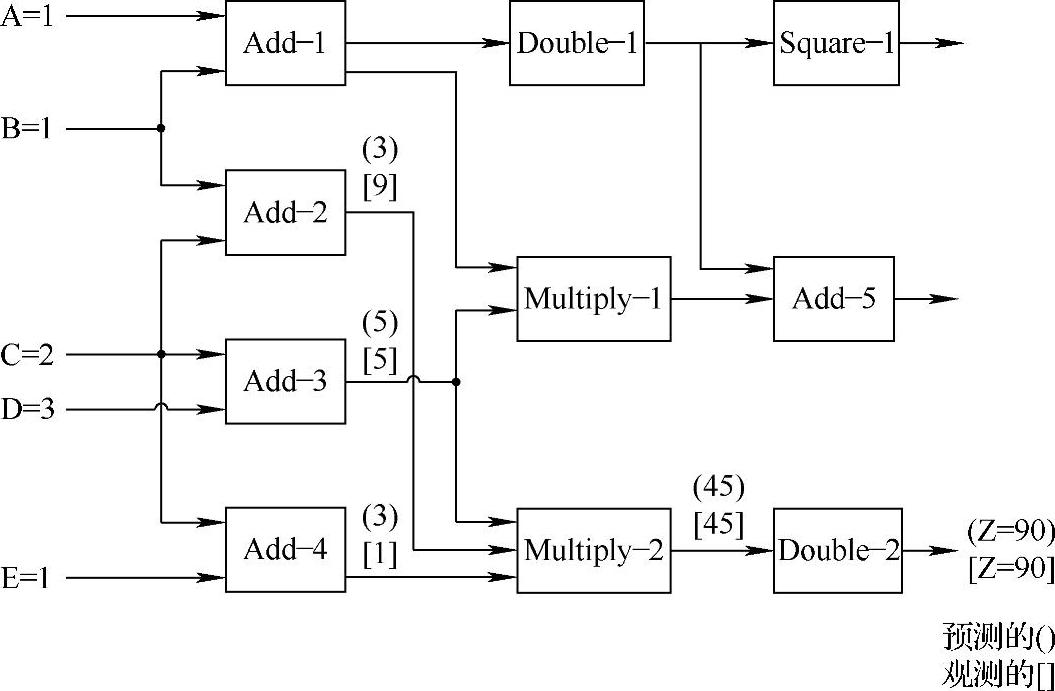
图7-5 Z处的故障屏蔽，多点错误

在图7-5中，一个多点错误出现——Add-2和Add-4。但是，故障屏蔽可能会在单点错误处出现，而且在仅有一个部件被中止时故障屏蔽的例子很容易构成。图7-6给出了仅有一处中止（Add-2）的简单故障屏蔽实例。部件Min读入两个输入且输出两者中的最小值。输出Z是一致的，因为Min对观测输入和预测输入是不敏感的[（Min（10，45）和Min（10，30）都是10）]。

规则4

我们可以使用更多的误差信息去进一步限制推测集。特别地，假定单点错误，对每一个误差可以产生一系列推测，我们取其交集。

在图7-7中，出现了两个误差：一个在输出X，一个在输出Y。X的上游部件是（Add-1，Double_1和Square-1）；Y的上游部件是（Add-1，Add_3，Multiply-1和Add-5）。两者的交叉就是Add-1。因此，通过应用这个规则，Add-1就是造成故障的原因。

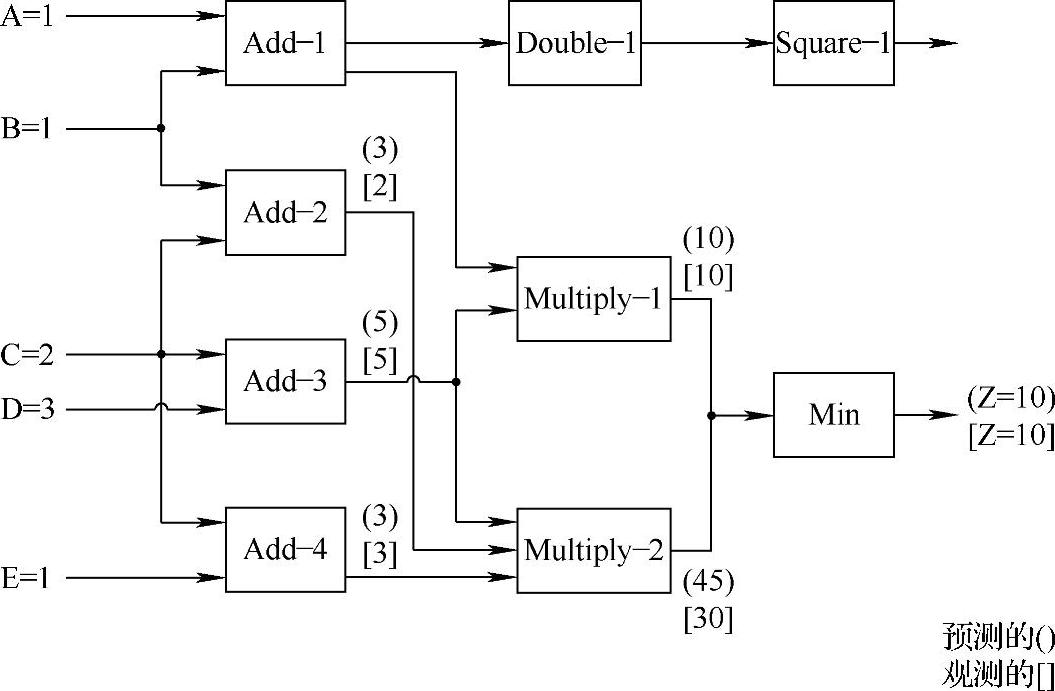
图7-6 在Z处的故障屏蔽，单点错误

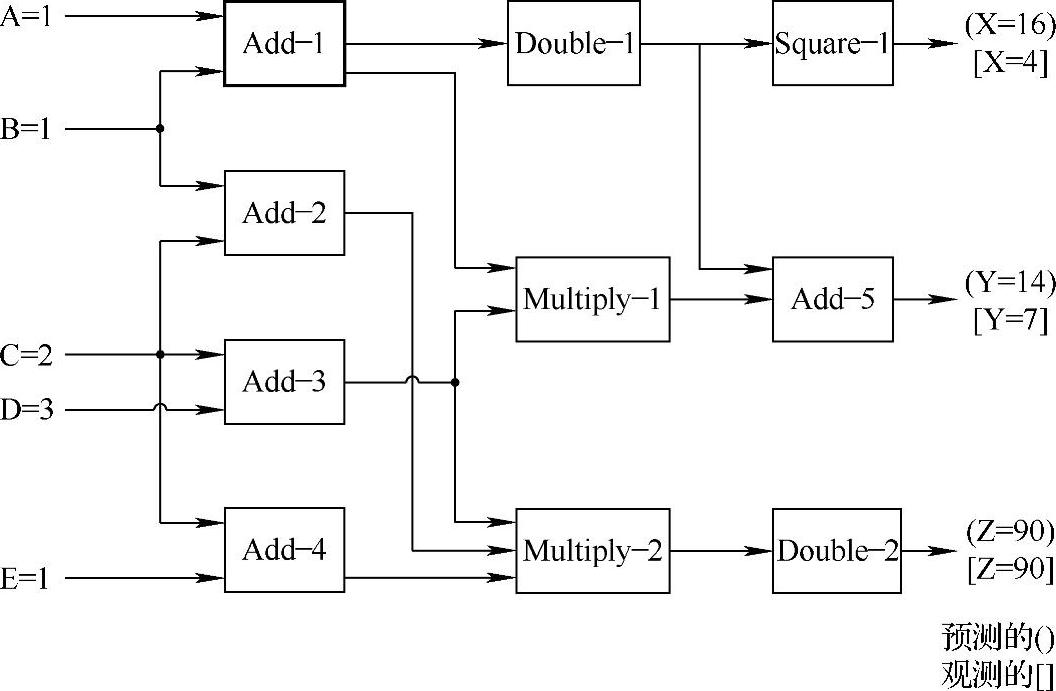
图7-7 X和Y上游集中的交叉

规则5

我们可以应用输出知识去限制推测集。

有时输出自然暗示着设备中的特定部件是有错的。例如，让我们假定图7-8的设备拓扑。Add部件使输入相加，Double部件将输入加倍，Subtract-one部件将输入减1。根据我们知识如果我们将一个整数加倍，它总是偶数，如果我们再将其减1，它就变成奇数，因此我们预报输出是奇数。反过来如果正如上面的情况它为偶数，则我们可以得出结论（Double和Subtract-one）就是一个推测集。我们甚至不需要将Add部件考虑成可能的推测，尽管它处在误差的上游。

图7-8 用于阐明输出如何影响推测集的简单设备

简单情况，在图7-2中给出的简单设备拓扑中，X必定是一个完全的二次方（4，16，25，36等），因为Square-1部件采用一个整数作为输入，并且输出该输入的二次方。如果它不是一个完全二次方，那么Square-1就是唯一逻辑推测。同样地，Z必定是一个偶数，如果它不是，则Double-2就是可能的推测。

即使当我们已经使用这5种规则去消除推测时，我们仍可能会有一个或更多的推测。诊断的第二步就是假设检验和辨别^[7]。我们需要通过附加观测（观测设备的输入和输出）或者修改设备的输入并在新的情况下观测（不同输入的检验）去采集额外的数据。我们的目标是选择引起误差的更多可能的推测。

让我们返回到由图7-4给定的设备。这里我们已经免除了好多设备部件，仅保留了两个，Multiply-1和Add-5（我们希望在应用了这5个规则后仅有少数部件保留在推测集中，以便我们可以将检验集中到这些部件上）。为了消除一个推测，我们必须采集额外的数据。例如，我们可以观测Multiiply-1的输入（2和5），并发现其输出是5而不是期望的10。这就说明Multiply-1是故障部件，假定是单点故障时，则说明Add-5运行正常。最后，如果推测是故障屏蔽的，一个好的办法是修改设备的输入，做附加的观测以确保输出是一致的。表7-2总结了本节列出的基于模型的诊断步骤。

表7-2 基于模型诊断步骤