为了使上一节中所给出的例子更加精确，我们需要在维恩图表上确定转换的规则。也就是维恩图表上所表示的是通过什么规则进行组合并控制的？我们的转换规则应该能正确地帮助我们如何去控制图表，以便我们能将一种图表转换成另一种等效的图表。

一种适当的类比是代数学规则，这种规则允许用代数等式去完成转换。例如：

A（B+C）=AB+AC（遵循分配律）=AC+AB（遵循加法交换律）=CA+BA（遵循乘法交换律）

就如同代数规则一样，转换规则将告诉我们允许的转换是什么，我们怎样能够一步一步地将一种图表转换成为另一种图表。

我们之前讨论了从一种图表中获得另一种图表的概念。我们需要使这些思想更加严密和完整。我们的转换规则将允许用更加精确的方式确定如何将一个图表（例如D₁）转换成另一个图表（例如D₂）。如果能够使用这些转换规则将图表D₁转换成D₂，那么就能够从D₁中获得D₂；同时，如果能够从D₁中获得D₂，这里D₁表示了前提，D₂表示了结论，那么就将有一个有效的推论。因而我们的转换规则就将能够使我们对确定推论有效性的过程进行明确的表达。此外，如果有精确的转换规则，我们就能够开发算法和计算机程序去为我们完成推论推理。

对讨论进行总结，将变化规则分为以下3种处理类型^[4]：

1）擦除一个对象；

2）添加一个对象；

3）将两个图表统一。

通过对象，我们明确地将3种对象类型中的一种表示在维恩图表上：（1）圆圈（集合）；（2）x-序列（非空）；（3）阴影（空）。

1.擦除一个对象

首先考虑了3种有效地擦除：在分隔区域中的一个完全的阴影；一个完整的x_-序列；当x-序列的一部分在阴影区域中时的部分x-序列。然后，考虑在维恩图表上擦除一个完整的圆圈。

规则I.1：在分隔区域中擦除阴影。可以擦除在分隔区域中的阴影部分。

规则I.2：擦除全部的x-序列。可以擦除全部的x-序列。

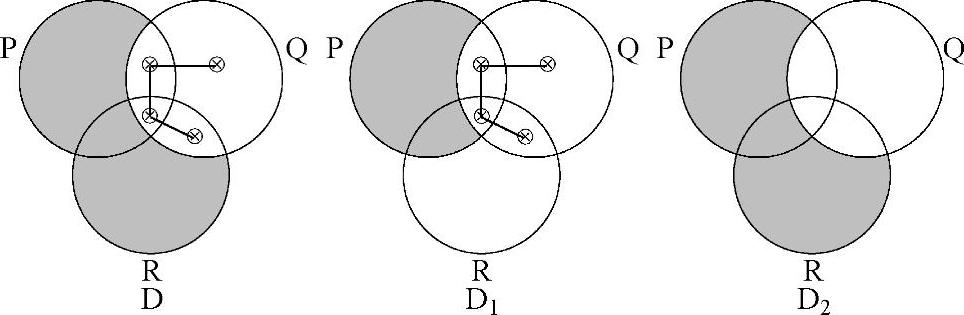
由于D₁擦除了在一个完整分隔区域中的阴影，因此D₁是D的有效变化（规则I.1）；由于D₂擦除了全部x-序列中的阴影，因此D₂是D的有效变化（规则I.2）。

规则I.3：在阴影分隔层中擦除部分x-序列。如果在阴影区域中，那么能够擦除x-序列中的任何。如果在x-序列的中间，那么当擦除了后，必须将剩下的部分连接起来，以便获得一个x-序列。在图表中x-序列的数量没有改变。

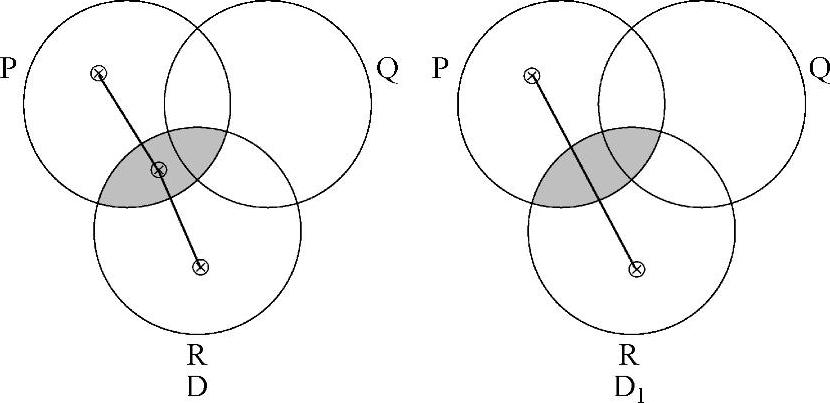
在这一图表中，从D到D₁的变化是有效的。首先擦除了在阴影区域中的，然后将两个保留的符号进行连接。

规则I.4：擦除圆圈。我们能够擦除全部圆圈。通过这一步骤，能够产生两种情况：（1）得到的维恩图表可能在分隔区域中包含部分阴影；（2）得到的维恩图表可能在分隔区域中包含超过一个的x-序列。

规则I.4.a：分隔区域中的部分阴影。当擦除圆圈，并且得到的维恩图表在分隔区域中包含部分阴影时，那么在那一分隔区域中的阴影就会被擦除。

在D中，能够擦除圆圈R，由此产生图表D₁。分隔区域1和分隔区域2包含部分阴影，这些阴影必须被擦除。D₂中给出了正确的转换。

规则I.4.b：在分隔区域中有超过一个的x-序列。当擦除圆圈时，得到的维恩图表包含一个x-序列，这一x-序列在分隔层中有超过一个，那么x-序列的一部分将由一个所取代，并且应该与其他的x-序列相互连接。

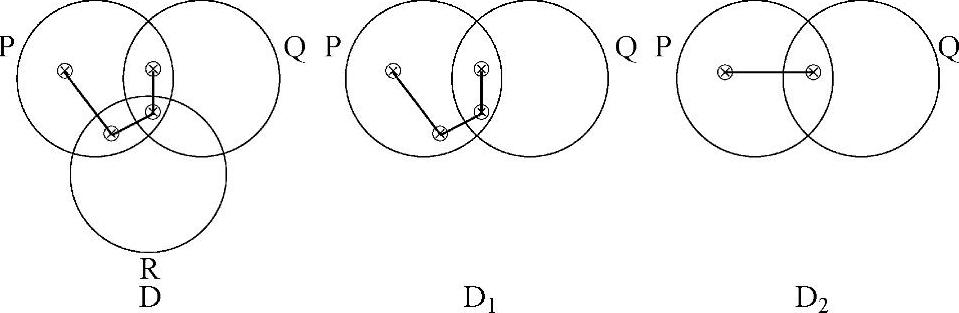
在D中，擦除了圆圈R，得到的维恩图表D₁中包含了含有两个符号的两个分隔区域。通过两次应用这一规则（对于每一个分隔区域应用一次），获得了D₂，这是对D的合理转换。

2.添加一个对象

两种类型的对象可以被添加到同一张图表中：可以添加任意数量的符号到一个存在的x-序列中，并且能够将一个圆圈添加入图表。添加阴影或是一个新的x-序列是无效的转换。

规则II.1：延长x-序列。我们能够将任意数量的符号添加到已有的x-序列中。图表中x-序列的数量将不会发生改变。

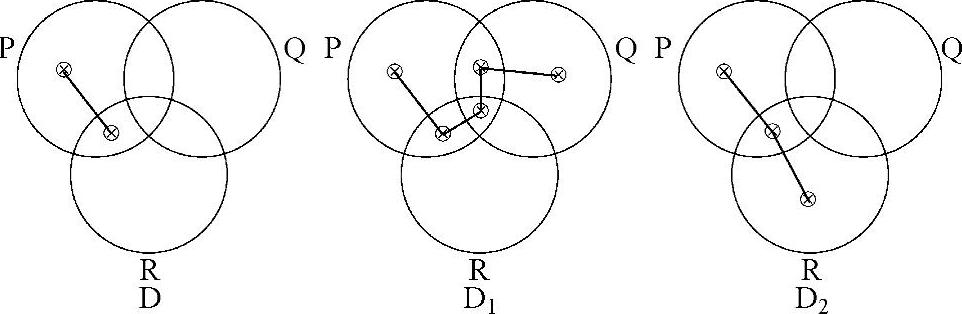
通过这一规则，D₁和D₂都是D的有效转换。(www.daowen.com)

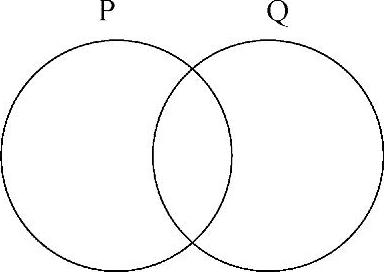
规则II.2：添加圆圈。我们可以将一个圆圈添加到维恩图表中。这必须满足部分重叠规则。如前所述，引入维恩图表的新的圆圈必须相互重叠，同时与图表的每一个分隔区域重叠一次，并且只能重叠一次。例如，假设有双子集维恩图表P和Q，将由两个重叠的圆圈所表示：

下图是当添加了第三个圆圈R时的无效转换：

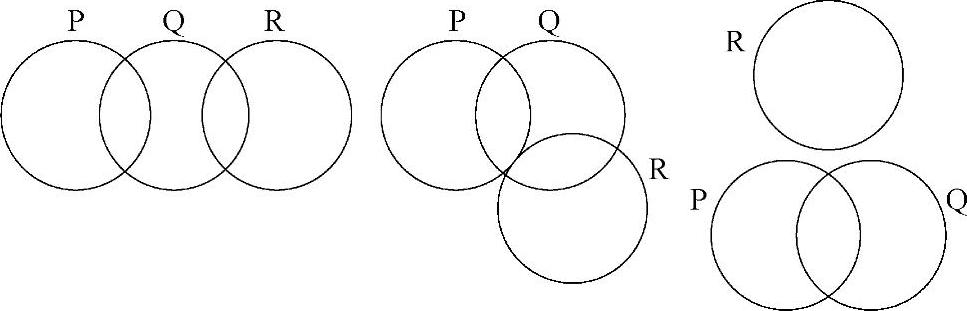
在所有的这些例子中，将圆圈表示的R引入维恩图表，圆圈R并不与每一个分隔区域重叠。下面的维恩图表表示了正确添加的第三个圆圈：

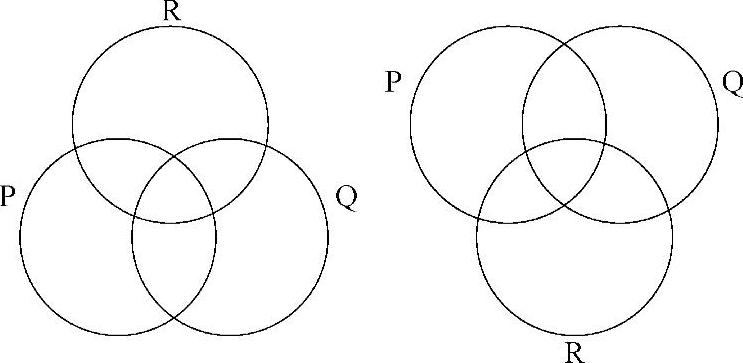
规则II.2.a：包含在x-序列中一个区域的全部分隔区域。当向维恩图表添加一个圆圈时，将会产生之前不存在的分隔区域。如果在最初的图表中有x-序列，那么必须为所产生的每一个新的分隔区域添加，这些分隔区域在最初的图表中部分区域包含。必须添加这些符号去形成单一的x-序列。在图表中x-序列的数量没有发生改变。

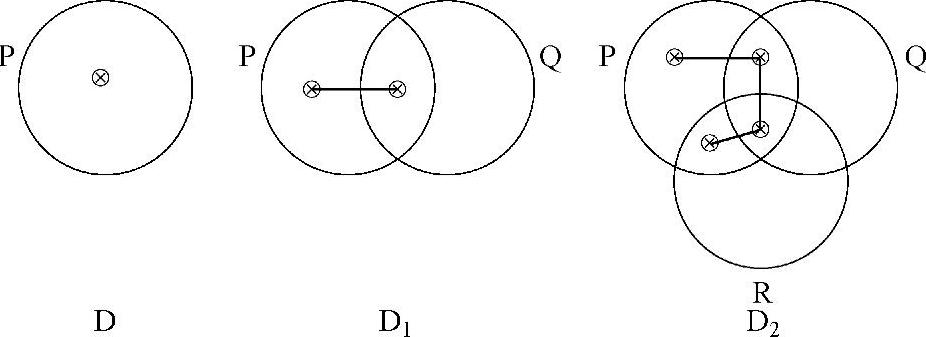
在这一例子中，图表D₁和D₂都是对D的有效转换。当圆圈Q添加到图表中时产生了D₁。在这种情况中，区域P包含了两个分隔区域，因而有两个相连接的符号。当圆圈R添加到D₁时产生了D₂。现在4个分隔区域组成了区域P，因而4个连接的符号形成了x-序列去表示在区域P中存在的事物。

3.将两个图表统一

可以将两个图表D₁和D₂统一到一个图表中。例如，在推论法推理中，如果结论来自假设，在能够确定之前需要合并两个假设。需要规则去指导如何正确地将两个图表合并成一个图表。这也称之为合并图表D₁+D₂。

规则Ⅲ.1：复制圆圈到统一的图表。首先从图表D₁中复制圆圈。如果在图表D₂中存在的圆圈在D₁中不存在，那么必须同样复制这些圆圈，并注意部分重叠规则（如规则II.2中所讨论的）。

规则Ⅲ.2：复制对应的阴影到统一图表。对于在D₁和D₂中的任何阴影区域，在D₁+D₂中对应的区域也应当是阴影的。

规则Ⅲ.3：复制对应的x-序列到统一图表。对于在D₁和D₂中任何具有x-序列的区域，应当在对应的D₁+D₂分隔层中画上x-序列，以便满足如前所定义的添加x-序列的规则（参见规则II.2.a）。

我们将通过一些特殊的例子说明这些统一。

例1

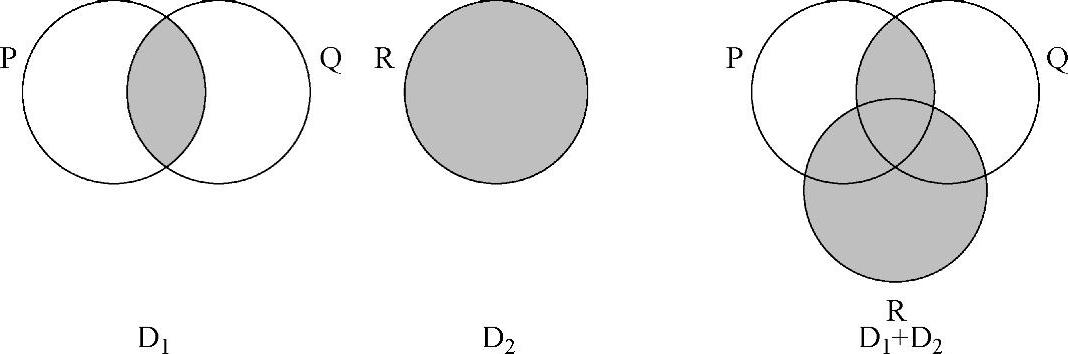
通过规则Ⅲ.1，我们复制了D₁和D₂中所含有的全部圆圈，并将其命名为P、Q和R。绘制这些圆圈以便它们满足部分重叠规则。通过规则III.2，将在D₁和D₂中所画阴影的部分，在D₁+D₂中对应的区域画上阴影。

例2

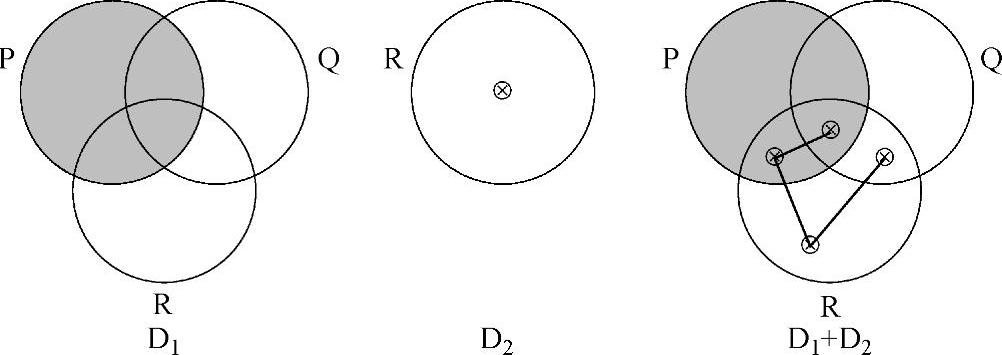
通过规则Ⅲ.1，首先从D₁中复制了所有的圆圈到D₁+D₂，并将其命名为圆圈P、Q和R。然后从D₂中复制所有的圆圈。由于圆圈R已经在图表上了，不需要添加任何额外的圆圈。通过规则III.2，将阴影复制到统一的图表中。通过规则III.3，从R中复制x-序列。由于在统一的图表中圆圈R包含4个分隔区域，需要将4个符号放到一起作为一个x-序列（规则II.2.a）。最后，通过规则I.3，能够擦除在阴影分隔区域中的任意部分的x-序列。因而，最终的转换可由下面的图形给出。

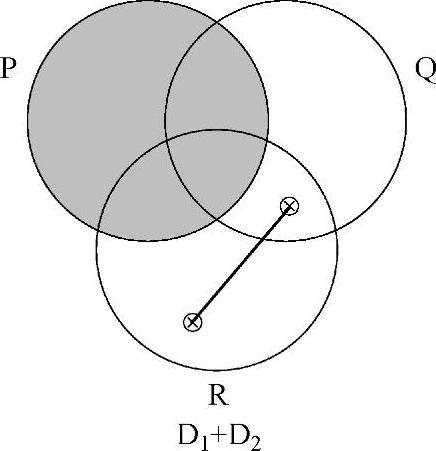
例3

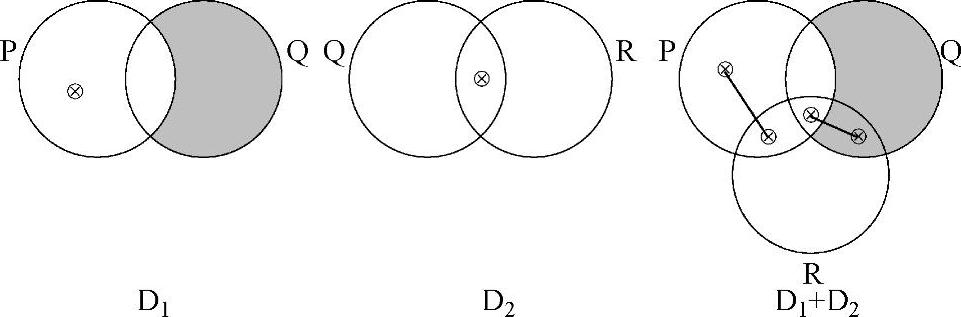
通过规则Ⅲ.1，并根据部分重叠规则，复制了圆圈P、Q和R到统一图表中。通过规则Ⅲ.2，复制了全部相应的阴影，在本例中是在图表D₁中的阴影。通过规则Ⅲ.3，能够复制全部相应的x-序列，一个来自于D₁，一个来自于D₂。规则II.2.a告知我们，需要将所有在x-序列中的相关分隔区域放到一起，因而需要在第一个x-序列放入两个符号，在第二个x-序列中放入两个符号。最后，通过规则I.3，能够除去在阴影分隔区域中的。最终统一的图表D₁+D₂由下图给出：

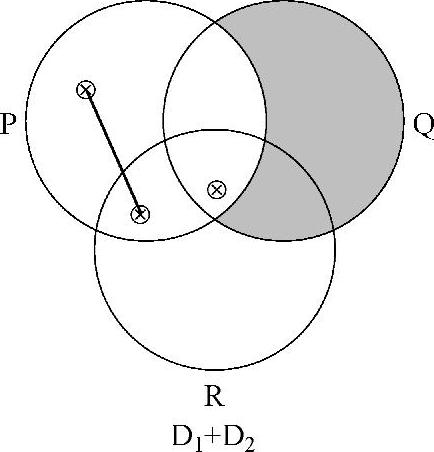
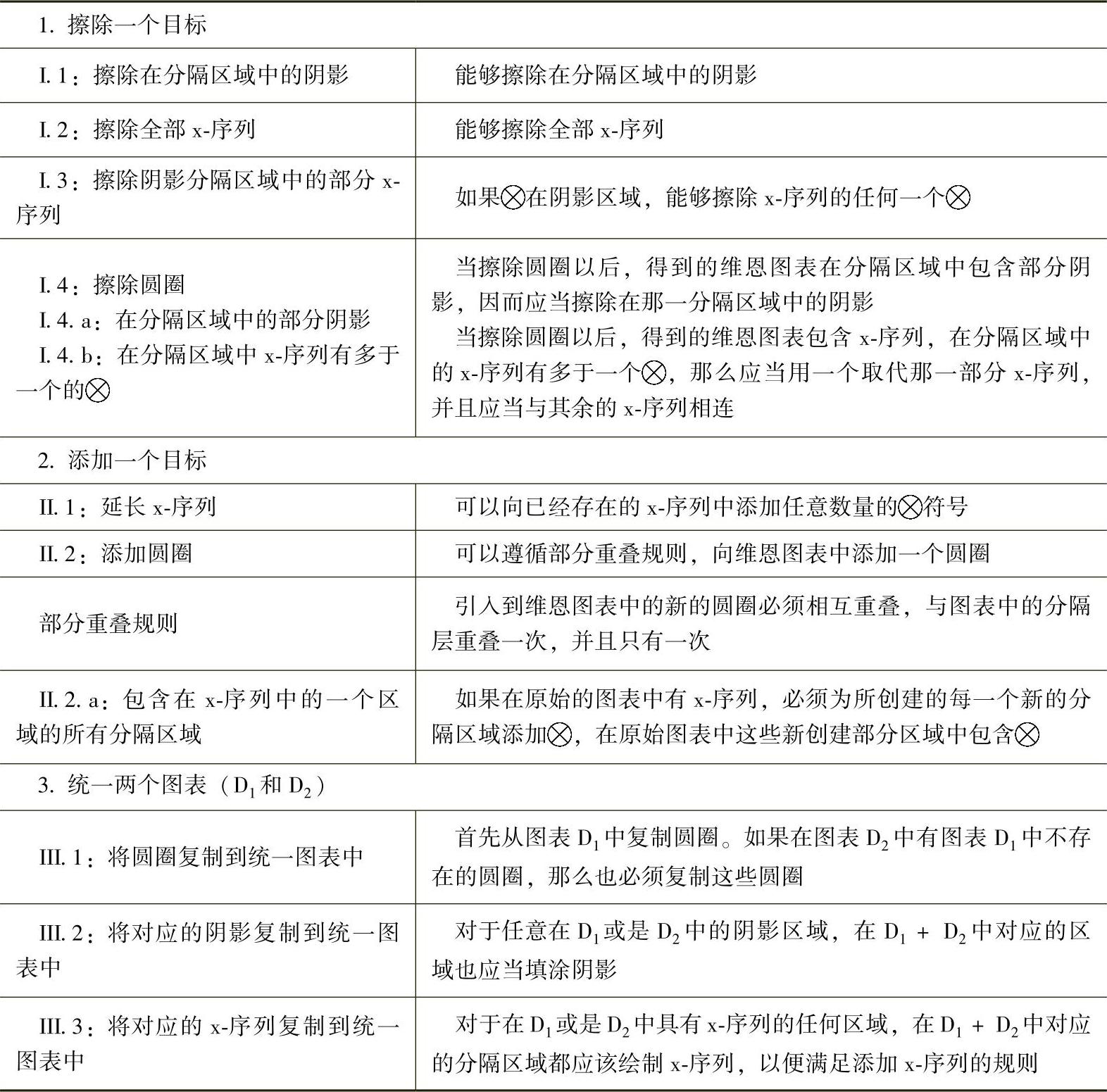
表4-1 总结了转换规则。

表4-1 转换规则