更为复杂的例子涉及了顺序决策情况，在这种情况中有一系列两个或是更多的决策点。图3-26是由下面的顺序决策情况所表示的决策树，这包括两个决策点：

假设你是一名勘探者，你必须决定哪个地点适合开采石油。从过去的经验中，你确定在你选择的地方有60%的机会能够有石油。你能够进行地震调查测试，以便提高知晓所在地是否蕴藏石油的机会。不幸的是，地震调查测试并不是100%精确，这是因为地震调查测试或是能够产生假阳性（当此地没有石油的时候，测试能够检测出石油的存在），或是能够产生假阴性（当此地实际上存在石油的时候，测试报告出没有石油）。如果测试结果是阳性的，那么此地确实存在石油的概率就有92%（有8%没有石油的概率）。如果测试结果是阴性的，就有25%的概率存在石油（有75%的概率没有石油）。你可以推测出有52%的概率是阳性测试，有48%的概率是阴性测试^[11]。

测试的成本是100000美元，所以你必须决定你是否想进行这种测试。你已经评估出在此地开采石油的成本是600000美元。你也已经评估出如果你确实决定开采，并且发现了石油，那么你将会获得2000000美元的石油租借回报。如果没有发现石油，那么此地点就是毫无价值的。

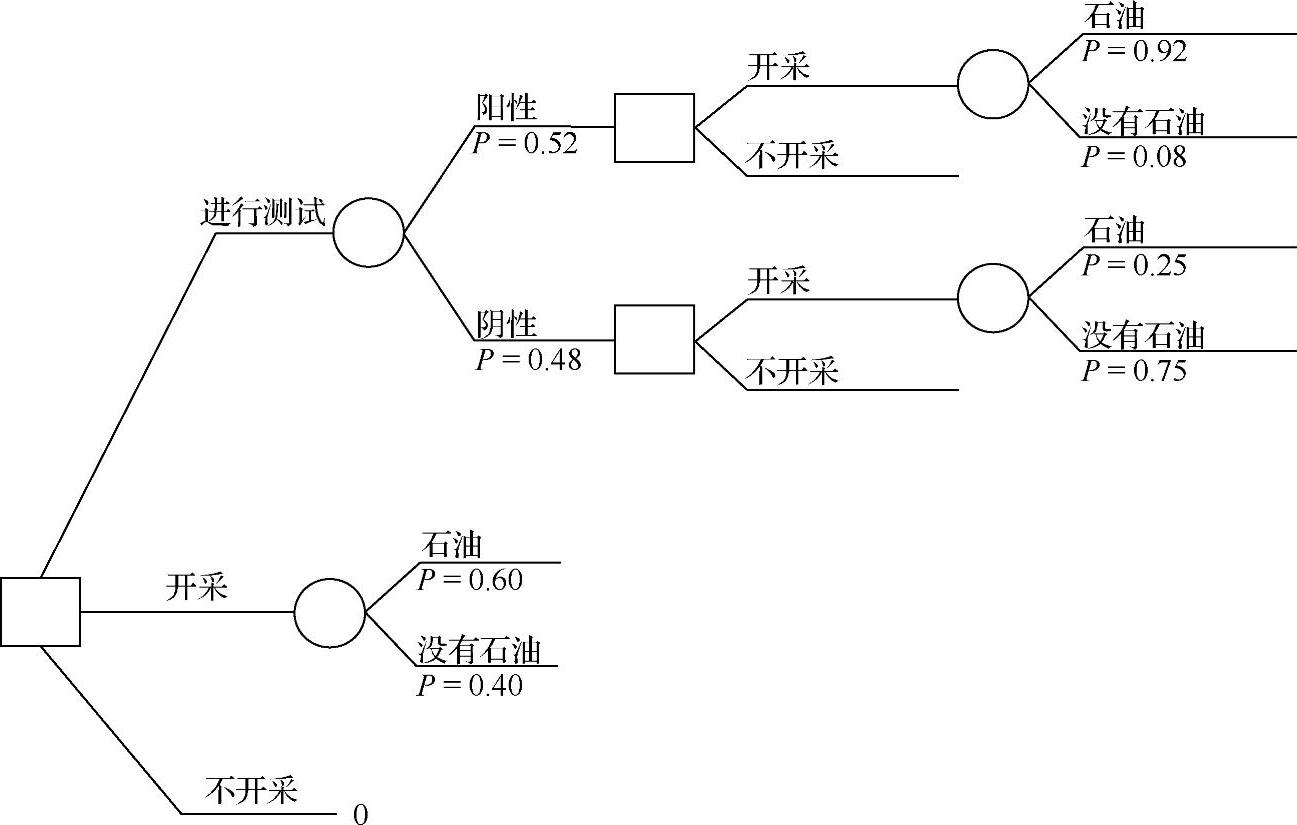
图3-26 表示顺序决策的决策树

在决策树中，我们从左侧的第一个决策节点开始，并且向右方开展我们的工作。在这里，勘探者面对着三种选择：（1）进行测试；（2）开采石油；（3）不开采石油。选择2和选择3是直截了当的。如果勘探者决定开采石油，并且发现了石油，那么回报就是1400000美元（2百万美元减去60万美元的开采成本），同时如果没有发现石油，回报是-60万美元，去弥补开采成本。

如果勘探者选择进行测试，在知晓测试结果之后就会出现第二个决策点。在这一点上，树的分支分成两个部分，这意味着勘探者能够依靠地震测试产生的阳性或是阴性结果去做出不同的决定。如果发现了石油，那么在树的这一分支中的收益是1300000美元（2000000美元减去开采和地震测试成本），如果没有发现石油，收益是-700000美元（开采和地震测试成本）。

为了求解决策树，你可以从反方向处理：可以从决策树的右方开始，向着左方进行处理。可以计算每一个可能节点的期望值，并且经过最大期望值到达决策节点。可以连续进行这项工作，直到到达最左侧的根部节点。完整的求解过程如图3-27所示。

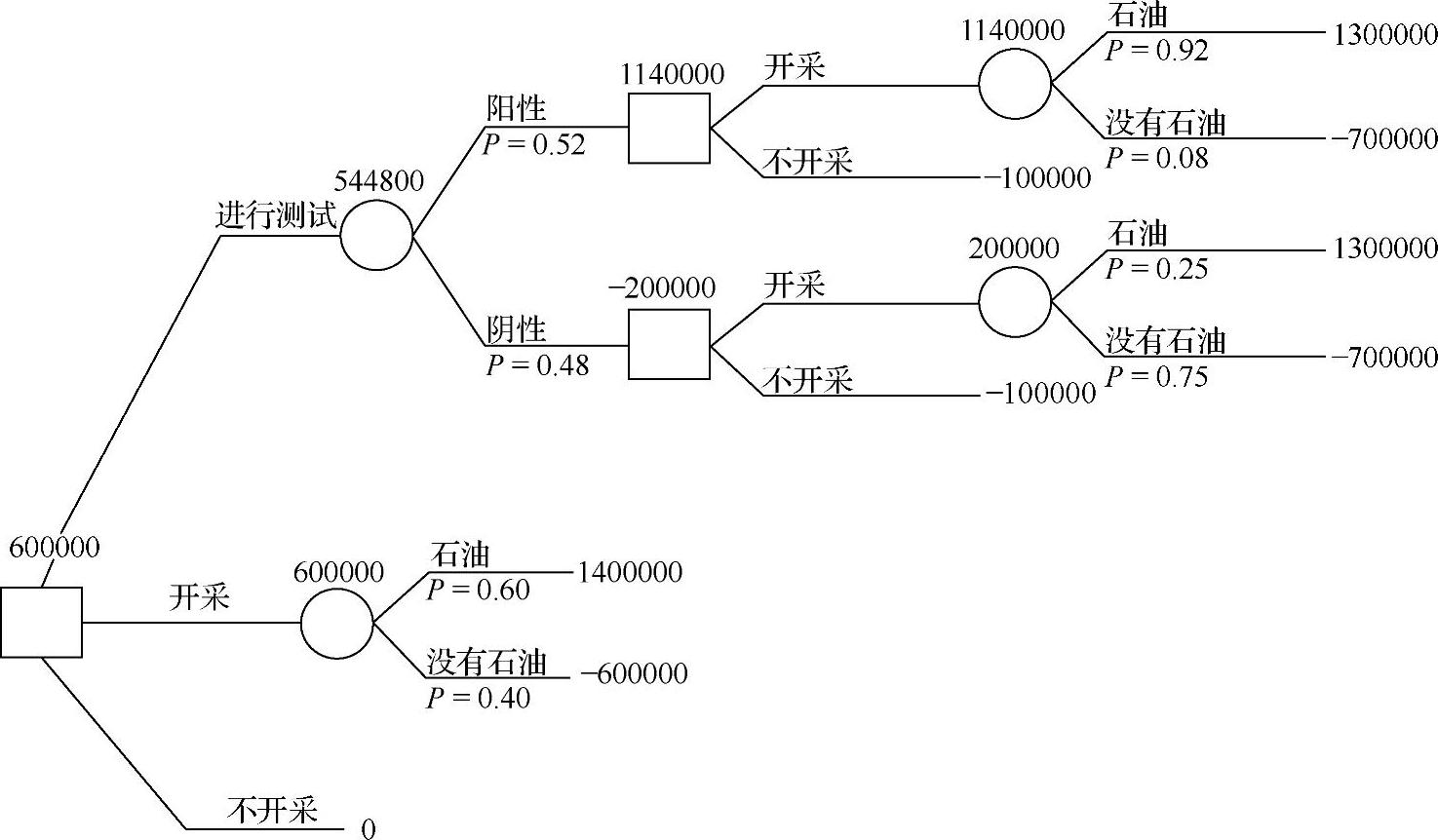
图3-27 顺序决策的求解过程图表

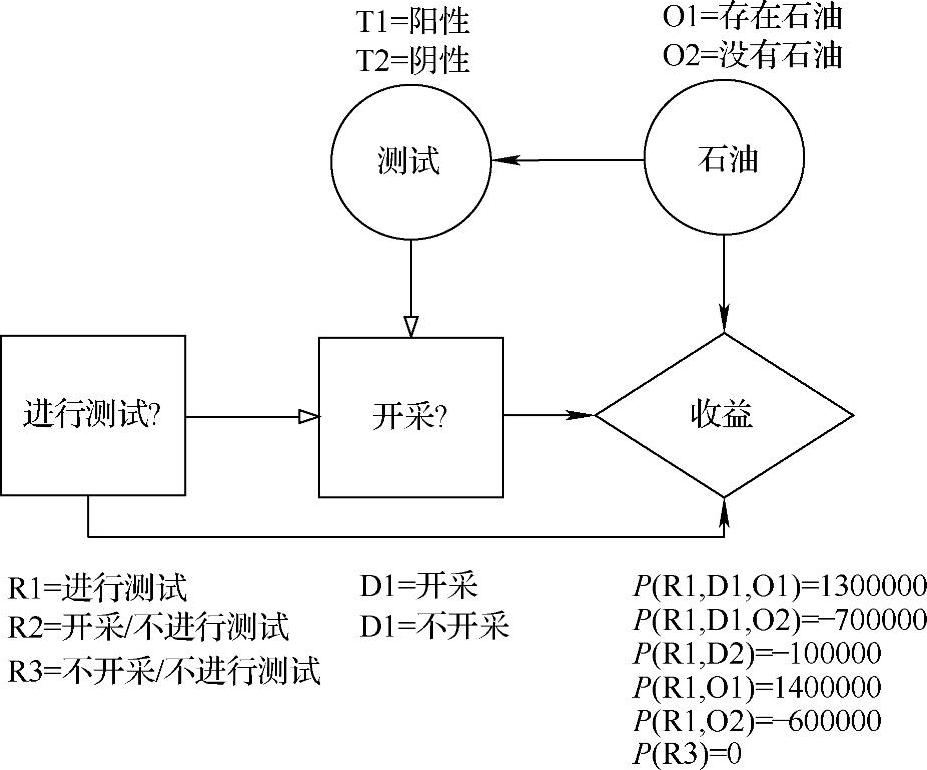
图3-28 顺序决策的影响图表(www.daowen.com)

仅仅基于期望收益，勘探者将能够进行开采（不用进行测试实验）。对于这一选择的期望收益是600000美元，这相对于下一个最好的选择（进行测试实验）所获得544800美元的期望收益。虽然进行测试实验获得了更低的期望收益，但是进行测试实验有较低的风险。如果获得阴性测试结果，你可以决定不去进行开采，结果是仅仅得到100000美元的预期损失。另一方面，如果你不去进行测试，将有很大的概率（0.4）损失掉600000美元。

图3-28中描绘了对于石油勘探决定的影响图表。这一图表包括两个决策节点（“进行测试实验？”和“开采？”），以便表示决策情况的连续特性，包括两个可能节点（“测试”和“石油”），并且包括表示勘探者将会获得或是取得净美元数这一结果节点（“收益”）。如同前面在图3-25中所给出的例子，对影响图表进行注释，以便表示每一个节点的可能值是多少。

图3-28表示了“回报”节点由其他三个节点：“进行测试实验？”、“开采？”和“石油”所影响。如果你很难理解为什么由这些节点影响，那么你可以思考一下图表给出的收益值。“收益”的值由这三个节点决定。例如，P（R1，D1，O1）=1300000。如同在图3-25中的图表中所给出，对于“进行测试实验？”、“开采？”和“石油”三个节点的相应的组合，写出其收益值将有助于理解它们是如何影响收益的。最后，有一个从“石油”到“测试实验”的箭头。这个箭头表示了是否存在石油将会对测试结果产生影响（如果存在石油，你更可能得到阳性测试结果；如果没有石油，你更可能得到阴性测试结果）。

在图3-28的影响图表中，我们也可以引入一种新的符号：

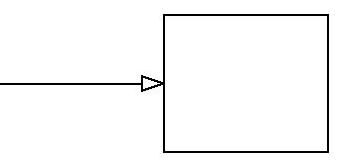
这一在右边有空心箭头的一条线的连接表示了顺序，而不是影响^[12]（用实心箭头表示影响）。在图3-28中，有两个连接表示了顺序。从“进行测试实验？”到“开采？”的线段表示了“进行测试实验？”的决定在“开采？”决定之前进行这一事实。

人们可能对为什么“测试”到“开采？”表示了顺序而不表示影响产生困惑。这是因为作出开采的决定是要知道地震测试的结果。从决策者的观点看，解决了“测试”这一可能事件，就不会有与之相联系的不确定性。因而，决策遵循着地震测试实验。通常，与其他节点相连接的前一节点（无论是否是决策节点或是可能事件）总是表示了顺序。在所引入的表示顺序和影响的符号中，正确地建立的决策图表中不允许出现下面的表示：

既然我们对决策树和影响图表有了理解，那么如何对两个绘制图表方法进行对比，并且就给出的做出决策的情况而言哪种图表更好呢？所给出的例子显示出决策树比影响图表能够表示出更多的细节。这意味着随着问题解决的情况变得更加复杂，决策树倾向于变得更加难于处理。因而，如果你的目标仅仅是表达决策情况的要点，那么影响图表就可能更加合适。

另一方面，决策树能够更加清晰和具体地说明决策情况的变化。特别是当显现决策节点的顺序和偶然性事件是如何影响你的结果的时候。在这一方面，去想象节点从左到右按着时间的顺序依次发生是十分有用的。因而，我们能够通过决策树去追溯路径，以便理解一系列的决策和偶然事件是如何产生一个特别的结果。那么，就解释能力而言，决策树要优于影响图表。

与其将一种方法看做是比其他方法更为可取的，要采取更好的态度可能是将两种方法作为对方的互补。根据这一观点，使用两种方法比单独使用一种方法的效果要好。事实上，我们总是能够从影响图表中生成决策树，反之亦然。就相同的决策情况，两种方法能够提供不同的观点。一种方法能够加强另一种方法，在很难搞清楚决策环境的时候，两种方法一起使用能够为理解什么是最重要问题的决策者提供更加清晰的思路。