在决策树中，有两种类型的节点：方形代表决策点，圆形代表偶然事件（见图3-24）。从方形延伸出的分支表示了对于决策者的可选择变量，从圆形延伸出的分支表示了偶然事件的可能结果。图3-24表示了下面投资过程的决策树。

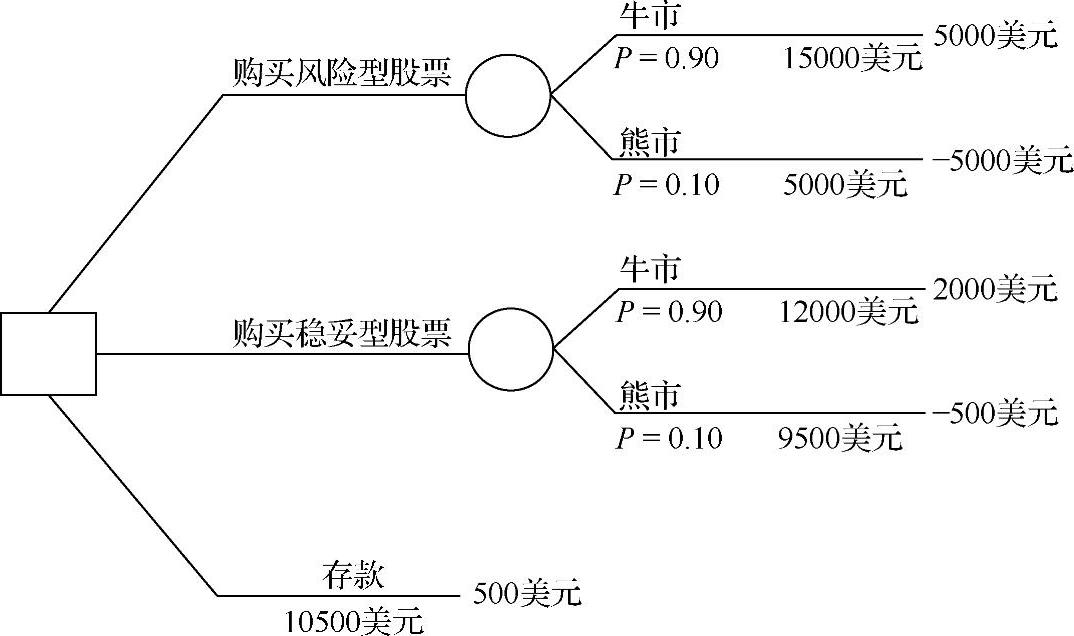
图3-24 简单的决策树

假设你有10000美元去投资。你可以投资到下面的一个项目中：风险型股票、稳妥型股票或是存款。如果你投资到了风险型股票，那么如果是牛市，股票将会增加50%到15000美元；如果是熊市，股票就会缩水50%到5000美元。另一方面，如果你投资到了稳妥型股票，那么如果是牛市，股票将会增加到12000美元；如果是熊市，股票就会缩水到9500美元。最后，你也可以进行存款，这将保证你获得5%的利率或是500美元。如果我们假设有90%的牛市机会和10%的熊市机会，那么你将会选择投资哪种项目呢？

在图3-24中，有三种选择：购买风险型股票，购买稳妥型股票，或是存款，从投资决策节点中分支出来，并且有两种偶然结果：牛市和熊市从每两种节点中分支出来。需要指出的是，也存在与每一个结果联系的可能性，同时它们必须总是对每一个偶然节点增加到1。这是因为，我们假定结果是互斥的，并且是详尽列举的（这意味着没有其他可能的结果）。最后，我们最大限度地包含对于每一种结果的投资回报。

求解决策树的一种方法是对于三种选择中的每一个计算出其投资回报的期望值：

E（风险型股票的回报）=0.9（5000）+0.10（-5000）=4000

E（稳妥型股票的回报）=0.9（2000）+0.10（-500）=1750

E（存款的回报）=500

如果你是一个期望值的最大化者——就是选择能获得最高期望值的决策者，那么你就将选择风险型股票。如果你要投资的资金数量相对于你的全部财富而言很少，那么这就将是所做出的一种合理选择。然而，如果你是一名更低风险投资者，那么如果你面对不能接受的风险水平，你就不会选择最高期望回报的投资。在这种情况中，你可能选择稳妥型股票，这样你的潜在损失就会比较低，或是选择存款，由于无论情况怎样你都能保证获得500美元的回报，因此这也是三种选择中最安全的一种。(www.daowen.com)

存在衡量或量化风险的方法么？一种方法是使用众所周知的效益函数。通过效益，我们可以看到决策者重视什么，这就是哪种方式可以获得或者不能获得收益。在我们的例子中，合适的效益函数将收益（在我们的实例中，是投资回报）对应与另一个评估风险的值（经济学家将这个值定义为效益）。这样的效益函数^[18]可以通过下式给出：

U_R（x）=1-e^-x/R

在这一函数中，将R称作抗风险程度，这确定了决策者的耐受风险程度：更小的R值将模拟了抗较低风险的决策者，较大的R值将模拟更加寻求风险的决策者。例如，让我们假设R=1000，这样我们能够计算三种选择的期望效益，如下：

EU（风险型股票）=0.9×U₁₀₀₀（5000）+0.1×U₁₀₀₀（-5000）

=0.9（1-e^-5000/1000）+0.1（1-e^5000/1000）=-13.85

EU（稳妥型股票）=0.9×U₁₀₀₀（2000）+0.1×U₁₀₀₀（-500）=0.9（1-e^-2000/1000）+0.1（1-e^500/1000）=0.6063

EU（存款）=1.0×U¹⁰⁰⁰（500）=1.0（1-e^-500/1000）=0.3935

因而，当R=1000的时候，稳妥型股票的期望效益是最高的。当R=300的时候，你可以选择存款收益作为替代，这是由于存款的期望收益是最高的（风险型股票、稳妥型股票和存款的收益分别是-1730777.00，-1.804和0.8111）。