对人工智能的难点和制造一台能思考的机器的困难的另一个解释在于涉及它的许多问题是难以驾驭的。这种难以驾驭指的是计算上十分困难（如果使用目前已知的算法是能够进行求解的）的问题。然而，人工智能程序的问题在于缺乏几乎是所有人（甚至是儿童）所拥有的对于普通问题求解能力的常识性推理，这些难以驾驭的问题会涉及更加复杂和专门的问题求解任务（例如玩象棋）。

在人工智能历史的早期，大多数研究的努力是关注于十分简单的小问题，也就是一些微观的问题，这样计算的复杂性问题就不是主要考虑的方面。一个很好的例子是“积木世界”。这一研究领域是将一组积木（例如正方形块，锥形块，球形块等）放置到桌面上，典型的任务是命令机器手臂以某种方式重新排列积木。例如，“将锥形块放置到最大积木的顶部。”SHRDLU^[3]是一种自然语言程序，这一程序允许用户与“积木世界”进行交互^[11]。用户编写SHRDLU命令去操作在积木世界中不同的对象。由于积木世界十分简单，所以程序在计算上是可行的：整个对象组可以由50个单词进行描述，从名词，如“木块”和“锥形块”，到形容词，如“小的”和“红色的”。不幸的是，当时的研究人员没有能够意识到如果这样简单的小问题按比例地提高到一个更加现实和复杂的问题求解领域，那么在计算上就会变得是难以驾驭的。

难以驾驭的特性对于人工智能和计算机科学领域具有巨大的影响。那些给了很多早期的人工智能预言者惊愕的许多问题已变成是十分难以解决的问题，这些事件的变化极大地限制了人工智能的发展。一个说明了难以驾驭特性的经典例子就是众所周知的旅行推销员问题。在这个问题中给出了n个城市、城市之间的路径和两个城市之间的距离如图1-4所示。这一问题是要寻找访问每一个城市的最短的路程，并且能够回到起始城市。

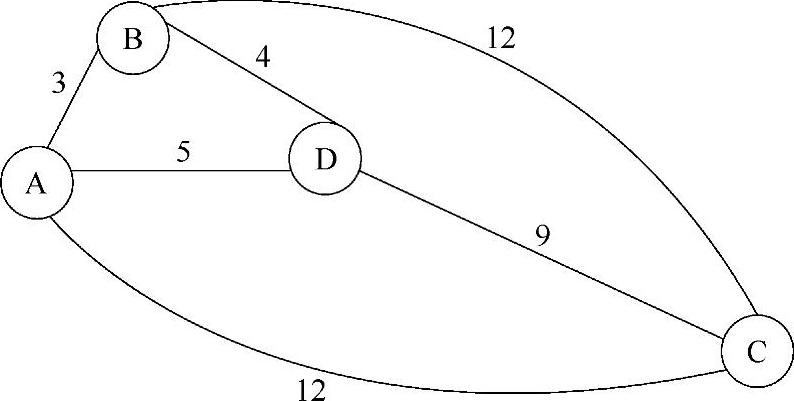
图1-4 旅行推销员问题[如果给定了四个城市A、B、C和D，这一问题的解决方案是什么？答案是：ACDBA（28mile^[4]）]

通过Brute Force搜索解决这一问题是一种简单的方式——这就是试图找出城市的每一种可能的次序，并且选择全部英里数最少的一种路径。仅仅当问题的规模很小的时候使用这种方法能够较好地进行工作，但是问题会很快变得难以驾驭。对于n=4的情况，你将需要计算出4！排列或是24种可能性^[5]。通常，对于n个城市的问题，你将需要计算出n！种排列。随着n的增加，问题规模将会迅速增长。例如，对于n=10的城市，你将需要计算出360000000种排列；对于n=20的城市，问题的复杂性将增长到2.4×10¹⁸种排列。很明显，即使是当今运行速度最快的计算机，对于足够大的数值n，Brute Force搜索策略也将会很快陷入困境。

那么如何定义难以驾驭性呢？一个定义就是，如果解决问题所需要的时间随着问题的规模呈几何增长，那么这一问题就是难以驾驭的^[12]。通过定义指数时间，我们从数学上表示出计算时间T（n）是问题规模n的函数，同时，存在常数c＞1，形如：

T（n）=O（cⁿ）(www.daowen.com)

相比之下，多项式时间函数在时间的复杂性方面是更加令人满意。在数学上可以表示成如下形式：

T（n）=O（n^k）

指数时间函数的例子包括2ⁿ和3ⁿ。多项式时间函数的例子包括n（线性时间）、n²（二次方时间）和n³（三次方时间）。

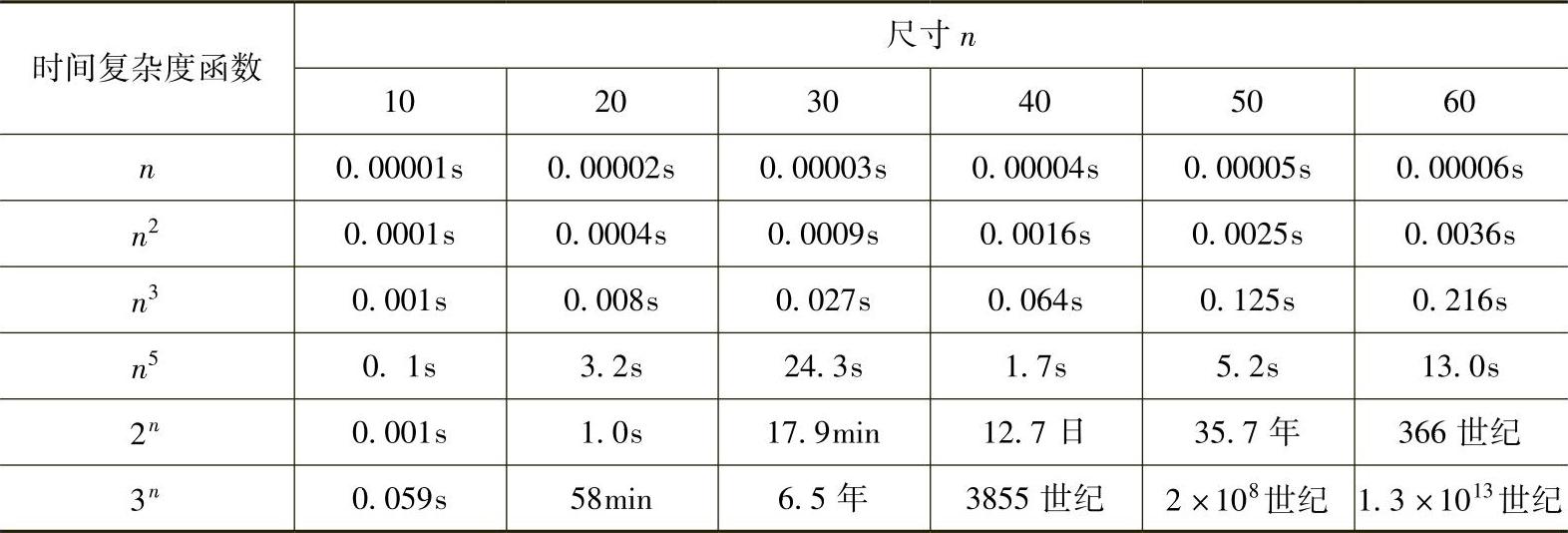
表1-1中给出了对多项式时间函数与指数时间函数的平行比较^[14]。在此表中，函数以微秒的方式表示了执行时间。这里所观察到的有趣的事情是与多项式时间函数相比较，指数时间函数所具有的极其快速的增长率。很明显多项式时间函数要比指数时间函数更好地满足要求。如同Gary和Johnson所指出的，大多数指数时间算法仅仅是在穷举搜索上的一些变化，而通过获取对问题结构更深入的看法通常才能获得多项式时间算法。人们取得了广泛的一致，认为直到引入了多项式时间算法后，问题才得到了很好的解决^[14][值得指出的是，通过使用动态编程和解决连续的决策结构问题的数学方法可以在时间O（n²·2ⁿ）内解决旅行推销员问题。虽然仍旧是指数时间算法，但这要优于O（n！）]。

表1-1 对一些多项式和指数时间复杂函数的比较（引自参考文献[13]）

对于难以驾驭问题的确定和论述不在本书的范围之内。本书中也不论述NP完全性理论^[15]——为了处理难以驾驭问题而建立的理论，并在涉及人工智能算法的许多权威书中都讨论了这一理论。在本书中，我们并不更深入地涉及对难以驾驭问题的讨论。当然，可以应用图表方法去更好地理解问题的结构，并通过给出足够好的解决方案（但并非必须是最优的解决方案）提出一些方法去建立启发式算法或经验法则，以便使其中的一些问题能够更加易于处理。在第7章中，我们使用了基于模型的推理，这种方法应用某些形式的图表模型，并从模型中得到的推理去帮助我们解决难以驾驭的问题，同时这一章中还提供了对如何找到解决问题方法的深入理解。