1.瞬时单位线

瞬时单位线是指流域上均匀分布的瞬时时刻（即Δt→0）的单位净雨在出口断面处形成的地面径流过程线。其纵坐标常以u（0，t）或u（t）表示，无因次。瞬时单位线可用数学方程式表示，概括性强，便于分析。

J.E.Nash设想流域的汇流可看作是n个调蓄作用相同的串联水库的调节，且假定每一个水库的蓄泄关系为线性，则可导出瞬时单位线的数学方程为：

式中 u（t）——t时刻的瞬时单位线的纵高；

n——线性水库的个数；

Γ（n）——n的伽玛函数；

e——自然对数的底，e=2.71828；

K——线性水库的调节系数，具有时间单位。

单位线的上述两个基本假定同样适用于瞬时单位线。瞬时单位线与时间轴所包围的面积为1.0，即

显然，决定瞬时单位线的参数只有，n、K两个。n越大，流域调节作用越强；K值相当于每个线性水库输入与输出的时间差，即滞时。整个流域的调蓄作用所造成的流域滞时为nK。只要求出流域的n、K值，就可推求该流域的瞬时单位线，如图7-8，图7-9所示。

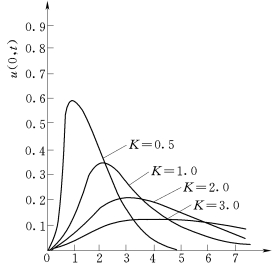
图7-8　K与瞬时单位线的关系

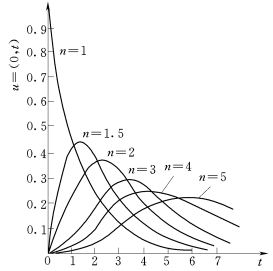
图7-9　n与瞬时单位线的关系

2.瞬时单位线的综合

瞬时单位线的综合实质上就是参数n、K的综合。但是，在实际工作中一般并不直接对n、K进行综合，而是根据中间参数m1，m2等来间接综合，m1=nK，m2=1/n。实践证明，n值相对稳定，综合的方法比较简单，如湖北省Ⅱ片的n=0.529F0.25 J0.2，江苏省山丘区的n=3。因此一般先对m1进行地区综合，根据已确定的n值就很容易确定出K值。

对m1进行地区综合一般是首先通过建立单站的m1与雨强i之间的关系，其关系式为m1=ai-b，求出相应于雨强为10mm/h（或其他指定值）的m1，（10）。然后根据各站的m1，（10）与流域地理因子（如F、J、L等）建立关系，m1，（10）=f（F，J，L，…），则m1=m1，（10）×（10/i）b，从而求得任一雨强i相应的m1。如湖北省Ⅱ片的m1，（10）=1.64F0.231L0.131 J-0.08。其次是对指数b进行地区综合。一般b随流域面积的增大而减小。有时也可直接对单站的m1—i关系式中的a、b进行综合，而不经m1，（10）的转换，如黑龙江省的m1=CF0.27i-0.31，C可查图得到。

3.综合瞬时单位线的应用

由于瞬时单位线是由瞬时净雨产生的，而实际应用时无法提供瞬时净雨，所以用综合瞬时单位线推求设计地面洪水过程线时，需将瞬时单位线转换成时段为Δt（与净雨时段相同）、净雨深为10mm的时段单位线后，再进行汇流计算。具体步骤如下：

（1）求瞬时单位线的S曲线。S曲线是瞬时单位线的积分曲线，其公式为

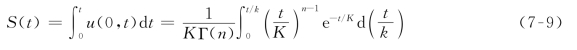
公式表明S（t）曲线也是参数n、K的函数。生产中为了应用方便，已制成S（t）关系表供查用，见附表5。

（2）求无因次时段单位线。将求出的S（t）曲线向后错开一个时段Δt，即得S（t-Δt）曲线。两条S曲线的纵坐标差即为时段为Δt的无因次时段单位线，其计算公式为：

（3）求有因次时段单位线。根据单位线的特性可知，有因次时段单位线的纵坐标之和为：；而无因次时段单位线的纵坐标之和为：∑u（Δt，t）=1.0。

有因次时段单位线的纵高qi与无因次时段单位线的纵高u（Δt，t）之比等于其总和之比，即

由此可知，时段为Δt，10mm净雨深时段单位线的纵坐标为：(www.daowen.com)

（4）汇流计算。根据单位线的定义及倍比性和叠加性假定。用各时段设计地面净雨（换算成10mm的倍数）分别去乘单位线的纵高得到对应的部分地面径流过程，然后把它们分别错开一个时段后叠加即得到设计地面洪水过程。

根据单位线的定义可知，单位线只能用来推求流域设计地面洪水过程线。湿润地区的设计洪水过程线还包括设计地下洪水过程线。如果流域的基流量较大，不可忽略时，则还需加上基流。所以，湿润地区的设计洪水过程线是设计地面洪水过程线、设计地下洪水过程线和基流三部分叠加而成的。干旱地区的设计地面洪水过程线就为所求的设计洪水过程线。

设计地下洪水过程线可采用下述简化三角形方法推求。该法认为地面、地下径流的起涨点相同，由于地下汇流较地面汇流缓慢，所以将地下径流过程线概化为三角形过程，且将峰值放在地面径流过程的终止点。三角形面积为地下径流总量Wg，计算式为：

而地下径流总量等于地下净雨总量，即Wg=1000hgF

式中 Qm，g——地下径流过程线的洪峰流量，m3/s；

Tg——地下径流过程总历时，s；

hg——地下净雨深，mm；

F——流域面积，km2。

按式（3-13）可计算出地下径流的峰值，其底宽一般取地面径流过程的2～3倍，由此可推求出设计地下径流过程。

【例7-3】江苏省某流域属于山丘区，流域面积F=118km2，干流平均坡度J=0.05，P=1%的设计地面净雨过程（Δt=6h）h1=15mm，h2=25mm，设计地下总净雨深hg=9.5mm，基流Q基=5m3/s，地下径流历时为地面径流的2倍。求该流域P=1%的设计洪水过程线。

解（1）推求瞬时单位线的S（t）曲线和无因次时段单位线。

1）根据该流域所在的区域，查《江苏省暴雨洪水手册》得n=3，m1=2.4（F/J）0.28=21.1，则K=m1/n=21.1/3=7.0（h）。

2）因Δt=6h，用t=NΔt（N=0，1，2，…）算出t，填入表7-5中的第①栏。

表7-5　设计洪水过程线计算表

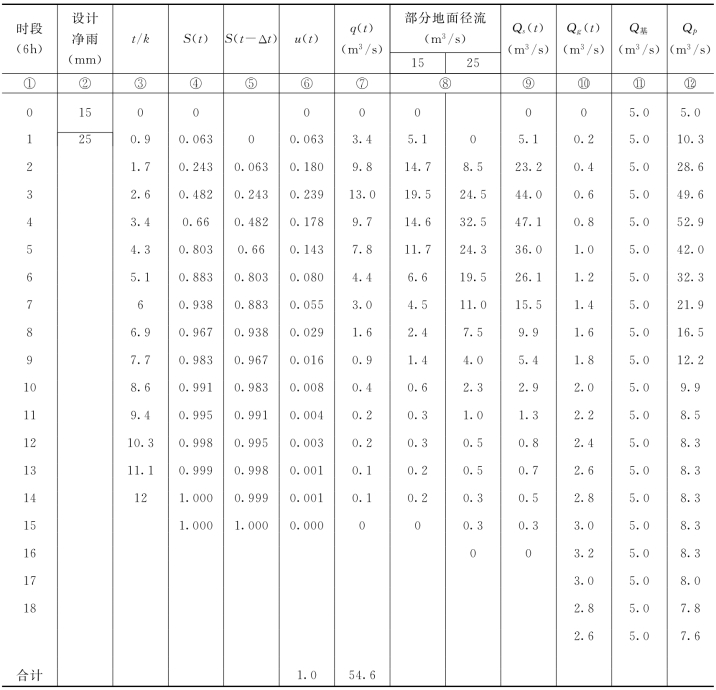
3）由参数n=3、K=7.0计算t/K，见第③栏，查附表5得瞬时单位线的S（t）曲线，见第④栏。

4）将S（t）曲线顺时序向后移一个时段（Δt=6h），得S（t-Δt）曲线，见第⑤栏，计算无因次时段单位线，见第⑥栏。

（2）将无因次时段单位转换为6h、10mm的时段单位线。

将第⑥栏中的无因次时段单位线转换为有因次的时段单位线，填入第⑦栏。

检验时段单位线：，计算正确。

（3）设计洪水过程线的推求。

1）计算设计地面径流过程：根据单位线的特性，各时段设计地面净雨换算成10的倍数后，分别去乘单位线的纵坐标得到相应的部分地面径流过程，然后把它们分别错开一个时段后叠加便得到设计地面洪水过程，见第⑧、第⑨栏。

2）计算设计地下径流过程：

Tg=2Ts=2×16×6=192（h）

据式（7-11）计算，得Qm，g=3.2m3/s，按直线比例内插的每一时段地下径流的涨落均为0.2m3/s。经计算即可得出第⑩栏的设计地下径流过程。

3）将设计地面径流、地下径流及基流[第⑩栏]相加，得设计洪水过程线。见第⑫栏。