设xi、yi代表两同步系列的观测值，共有n对，以自变量xi为横坐标值，以倚变量yi为纵坐标值，把它们的对应值点绘于方格纸上，得到很多相关点。如果相关点的平均趋势近似直线，则判定为简单直线相关，如图4-11所示，可以用图解法或计算法求出两变量的直线方程式

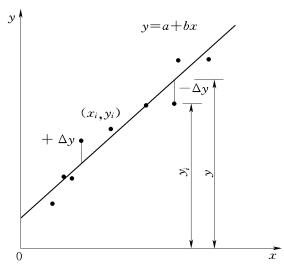
图4-11　简单直线相关示意图

式中 x——自变量；

y——倚变量；

a、b——待定常数，a表示直线在纵轴上的截距，b为直线的斜率。

1.相关图解法

先目估通过点群中间及点，绘出相关直线，然后在图上量出直线的斜率b，直线在纵轴上的截距a，则直线方程式y=a+bx即为所求的相关方程。该法简单实用，一般情况下精度尚可，但目估定线有一定的任意性，且缺乏一个定量的指标来判断两个变量间的密切程度。

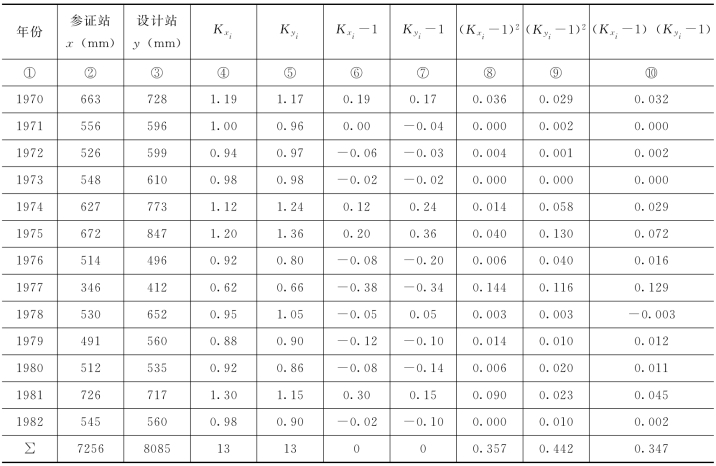
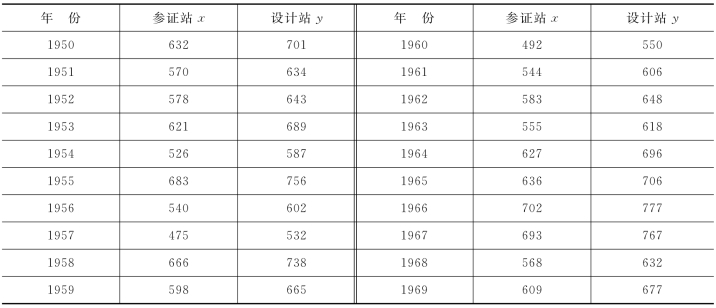
【例4-8】某设计雨量站有13年（1970～1982年）实测年降雨量资料，同地区有一邻近雨量站（称参证站）实测年降雨量资料系列较长（1950～1982年）。两站同步观测资料系列1970～1982年降雨量资料分别列入表4-6中第①、②、③栏。试用相关图解法建立相关直线方程，并将设计站年降雨量资料系列延长。

表4-6　某设计站和参证站年降雨量相关计算表

解 1）点绘相关图。将设计站年降雨量用y表示，参证站年降雨量用x表示。以y为纵坐标，x为横坐标，将表4-6中第②、③栏同步系列对应的数值点绘在普通格纸上，如图4-12所示，共得到13个相关点。由表4-6中第②、③栏总和分别计算x，y系列的均值：

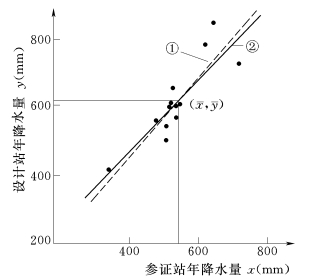
图4-12　某设计站和参证站年降雨量相关图

①—图解法；②—计算法

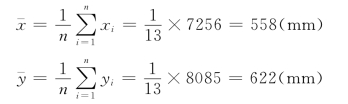
2）绘制相关直线。根据相关点的分布趋势，过点群中心并以均值点（558，622）为控制定出一条直线，如图4-12中线①。

3）建立直线方程。根据所绘直线，在图上查算出参数a=8，b=1.10，则直线方程式为：

y=1.10x+8

4）延长设计站年降雨量资料系列。将参证站1950～1969年的年降雨量值xi分别代入直线方程可求出相应的设计站年降雨量yi，见表4-7。

表4-7　设计站年降雨量展延成果表

2.相关计算法

为避免相关图解法在定线上的任意性，常采用相关计算法来确定相关线的方程，待定常数由观测点与直线拟合最佳，通过最小二乘法进行估计。

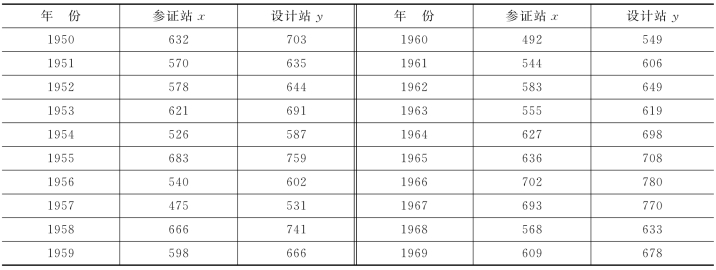
由图4-11可以看出，要使所定直线与实测点“最佳”拟合，就须满足各点距直线纵向离差的平方和最小，即使得

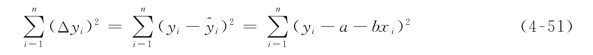
取极小值。

为了使式（4-51）取得极小值，可分别对a和b求一阶偏导数，并令其等于零，即：

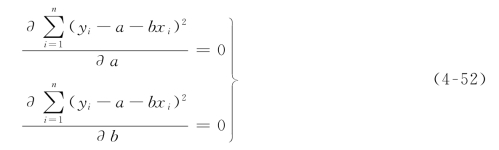
联立求解以上两个方程式，最后得到如下形式的相关直线方程：

式中 σx、σy——x、y系列的均方差；

——x、y系列的均值；

r——相关系数，表示x、y两系列间的密切程度，其计算式为

在水文统计中相关直线也称为回归线，所以式（4-53）又称为y倚x的回归方程，通过此方程式可以由自变量x的值来估计y。直线斜率称为y倚x的回归系数，记为Ry/x。若以y求x，则要应用x倚y的回归方程。同样，可以求得x倚y的回归方程式：

式中，称为x倚y的回归系数，记为Rx/y。(www.daowen.com)

一般y倚x与x倚y的两回归线并不重合，但有一个公共交点）。

3.相关分析的误差

（1）回归线的误差。回归线仅是观测点据的最佳配合线，通常观测点据并不完全落在回归线上，而是散布在回归线的两旁。因此，回归线只反映两变量间的平均关系。按此关系推求的估计值和实际值之间存在着误差，误差大小一般采用均方误来表示。如用Sy表示y倚x回归线的均方误，yi为观测值，为回归线上的对应值，n为系列项数，则

同样，x倚y回归线的均方误Sx为

回归线的均方误Sy与变量的均方差σy从性质上讲是不同的。前者是由观测点与回归线的离差求得的，后者则是由观测值与它的均值之间的离差求得。根据统计学原理，可以证明两者具有下列关系

由回归方程式算出的值，仅仅是许多yi的一个“最佳”拟合或平均趋势值。按照误差原理，这些可能的取值yi落在一个均方误范围内的概率为68.3%，落在三个均方误范围内的概率为99.7%，如图4-13所示。

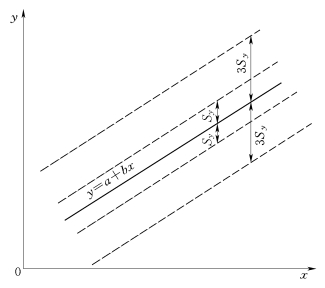
图4-13　y倚x的回归线的误差范围

必须指出，在讨论上述误差时，没有考虑样本的抽样误差。事实上，只要用样本资料估计回归方程中的参数，抽样误差就必然存在。可以证明，这种抽样误差在回归线的中段较小，而在上下段较大。

（2）相关系数及其误差。相关系数是反映两个变量r之间关系密切程度的指标。式（4-58）和式（4-59）给出了S与σ、r的关系，由此可知r2≤1，且有：

1）若r2=1，说明所有观测点都落在回归线上，均方误Sy或Sx等于0，两变量间具有函数关系，即完全相关。

2）若r2=0，说明两变量间不具有直线相关关系（零相关），则均方误达到最大值，Sy=σy或Sx=σx。

3）若0＜r2＜1，则介于上述两种情况之间，说明两变量间为直线相关，其相关程度密切与否，视r的大小而定。|r|越大，相关程度越密切，均方误Sy或Sx的值越小。r为正值表示正相关，r为负值表示负相关。

相关系数r不是从物理成因推导出来的，而是从直线拟合点据的离差概念推导出来的。因此，r=0时，只表示两变量间无直线相关关系，但可能存在曲线相关。

在相关分析中，相关系数是根据有限的实测资料（样本）计算出来的，必然会有抽样误差。一般通过相关系数的均方误σr来判断样本相关系数的可靠性，按统计学原理，相关系数的均方误σr可以由下列公式计算：

而总体不相关（r=0）的两变量，由于抽样原因，样本的相关系数不一定等于零。因此，在做相关分析计算时，首先应分析论证相关变量在物理成因上有密切的内在联系，用来建立相关关系的数据不能太少，一般n应在12以上，同时要求|r|≥0.8；回归线的均方误Sy小于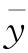的15%。在插补延长系列时，应注意回归线外延不应过长，还应避免辗转相关。

【例4-9】已知资料情况同[例4-8]。某设计雨量站有1970～1982年共13年的实测年降雨量资料，同地区有一邻近雨量站（称参证站）实测年降雨量资料系列为1950～1982年。试利用如表4-6第②、③栏所示两站同步观测资料进行相关计算，并展延设计站年降雨量资料。

解 为了便于相关计算，按表4-6顺序依次计算④、⑤、⑥、⑦、⑧、⑨、⑩栏，由表4-6的计算成果，可进一步算出以下各值：

1）均值：

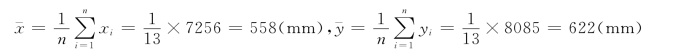
2）均方差：

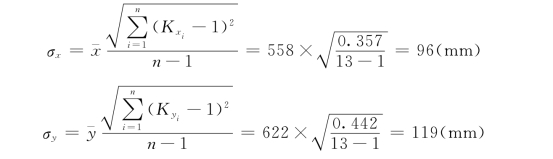
3）相关系数：

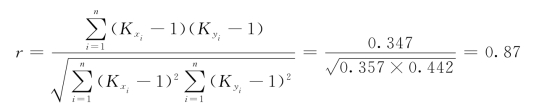
4）回归系数：

5）y倚x的回归方程：

6）回归直线的均方误：

7）相关系数的误差：

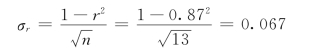
把参证站1950～1969年的年降雨量值xi分别代入回归方程中，可以算出对应的设计站年降雨量yi，见表4-8，从而使设计站和参证站的年降雨量资料系列具有同样的长度。

表4-8　设计站年降雨量展延成果表（mm）