客观世界中的随机变量具有不同的概率分布规律。经过研究和分析，可以对某些概率分布给出数学表达式，并得到相应的频率曲线。具有数学表达式的频率曲线称为理论频率曲线。因为水文变量的总体是未知的，而且又无法通过人工实验或理论分析等途径取得，所以分布函数的确切形式也是未知的，人们只能从数理统计的一些已知线型中，选择与水文现象配合好的线型，借用于水文实践中。所谓理论频率曲线只是一些具有数学表达式的频率曲线，把理论频率曲线用于水文分析计算，并不是已经从理论上严格证明了水文现象的概率分布应当服从某种理论频率曲线，用某种理论频率曲线描述水文变量概率分布仅仅是根据经验。我国水文工作中广泛采用的水文频率曲线是皮尔逊Ⅲ型分布。

1.皮尔逊Ⅲ（P-Ⅲ）型曲线

19世纪末期，英国生物学家皮尔逊对大量的物理、生物以及经济等方面的实验资料进行整理、统计，提出了13种随机变量的分布曲线线型。被引入水文计算中的就是其中的第Ⅲ种分布，根据经验，皮尔逊Ⅲ型分布曲线是与水文资料配合较好的线型，这种曲线在我国水文工作中被广泛采用，简称皮Ⅲ型曲线。皮尔逊Ⅲ型分布的概率密度曲线是一条一端有限另一端无限的不对称单峰、正偏曲线（图4-7），数学上常称伽玛分布，其概率密度函数为：

式中 Γ（α）——α的伽玛函数；

α、β、a0——皮尔逊Ⅲ型分布的形状、尺度和位置参数，α＞0，β＞0。

显然，3个参数确定以后，该密度函数随之可以确定。可以推论，这3个参数与总体3个参数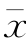、CV、CS具有如下关系：

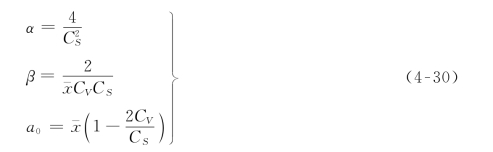
为了实际应用皮尔逊Ⅲ型分布，必须对它的概率密度函数进行积分，这样才能得到随机变量在某个区间取值的概率。在工程水文里，要计算水文变量的频率，即水文变量从某一个取值到正无穷大的概率，需要求出指定频率P所相应的随机变量取值xP，通过对密度曲线进行从随机变量的各个取值到无穷大的积分，即：

从而求出等于及大于xP的累积频率P值。

因皮尔逊Ⅲ型分布的概率密度函数十分复杂，水文计算中，直接由式（4-31）计算P值进行积分相当困难。为了能够在实际工作中运用皮尔逊Ⅲ型分布，可以通过变量转换，根据拟定的值进行积分，并将成果制成专用表格，从而使计算工作大大简化。

令

则有

Φ是标准化变量，称为离均系数。Φ的均值为0，标准差为1。这样经过标准化变换后，将式（4-33）、式（4-34）代入式（4-31），简化整理成下面的积分形式：

式（4-35）中被积函数只含有一个待定参数CS，其他两个参数x-、CV都包含在Φ中。因此，只需要假定一个CS值，便可从式（4-35）通过积分求出P与Φ之间的关系。对于若干个给定的CS值，ΦP和P的对应数值表，已先后由美国的福斯特和原苏联的雷布京制作出来，见附表1。

在频率计算时，由已知的CS值，查离均系数Φ值表得出对应于不同的频率P的ΦP值，然后利用已知的x-、CV，通过式（4-33）即可求出与各种P相应的xP值，从而可绘制出水文变量的皮尔逊Ⅲ型频率曲线。

为了更方便地进行频率分析计算，当CS等于CV的一定倍数时，有人根据皮尔逊Ⅲ型分布的离均系数表制作了模比系数表，见附表2。频率计算时，由已知的CS和CV可以从附表2中查出与各种频率P相对应的KP值，然后即可算出与各频率对应的xP=KPx-。有了P和xP的一些对应值，即可绘制出皮尔逊Ⅲ型频率曲线。

【例4-5】根据某地区年降雨量资料，求得统计参数和x-=1000mm，CV=0.5，CS=2CV，若该地区的年降雨量服从皮尔逊Ⅲ型分布，试求P=1%的年降雨量。

解 由CS=1.0，P=1%，查附表1得ΦP=3.02，由式（4-33）得：

或由CV=0.5，CS=2CV，P=1%，查附表2，得KP=2.51，算得：

2.频率曲线参数估计

在概率分布函数中都含有一些表示分布特征的参数，例如皮尔逊Ⅲ型分布曲线中就包含有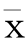、CV、CS三个参数。水文频率曲线线型选定之后，为了具体确定出概率分布函数，就得估计出这些参数。由于水文现象的总体是无限的，无法直接获得，就需要用有限的观测资料去估计总体分布线型中的参数，称为参数估计。

目前，由样本估计总体参数的方法主要有矩法、三点法、权函数法、概率权重矩法以及适线法等。这些方法各有特点，均可独立使用。我国工程水文计算中，通常采用适线法，其他方法估计的参数，一般作为适线法的初估值。

（1）矩法。矩法是用样本矩估计总体矩，并通过矩和参数之间的关系，来估计频率曲线参数的一种方法。该法计算简便，事先不用选定频率曲线线型，因此，是频率分析计算中广泛使用的一种方法。

设随机变量x的分布函数为F（x），则x的r阶原点矩和中心矩分别为：

和

式中 E（x）——随机变量x的数学期望；

f（x）——随机变量x的概率密度函数。

由于各阶原点矩和中心矩都与统计参数之间有一定的关系，因此，可以用矩来表示参数。

对于样本，r阶样本原点矩和r阶样本中心矩分别为：

和

式中 n——样本容量。

前面介绍过由前三阶样本矩表示的样本统计参数，均值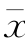的计算公式就是一阶原点矩，均方差σ的计算式为二阶中心矩开方，偏态系数CS计算式中的分子则为三阶中心矩。由此，得到计算统计参数的式（4-40）、式（4-41）、式（4-42）和式（4-43）。根据有限样本由这些公式计算出的参数与相应的总体参数不一定相等。但是，我们希望由样本系列计算出来的统计参数尽可能准确地估计出相应的总体参数。因此需将上述公式加以修正。

我们知道样本特征值的数学期望与总体同一特征值比较接近，当n足够大时，其差别更微小。经过证明，样本原点矩的数学期望正好是总体原点矩mr，但样本中心矩的数学期望不恰是总体的中心矩μr，要把经过修正后，再求其数学期望，则可得到μr。这个修正的数值称为该参数的无偏估计量，然后应用它作为参数估计值。于是得到修正后的参数计算式为：

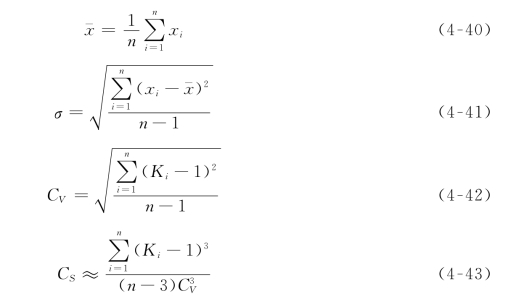
水文计算上习惯称上述公式为无偏估值公式，并用它们估算总体参数，作为适线法的参考数值。

必须指出，用上述无偏估值公式算出来的参数作为总体参数的估计时，只能说有很多个同容量的样本资料，用上述公式计算出来的统计参数的均值，可望等于相应总体参数。而样本只是总体的一部分，对某一个具体样本，计算出的参数可能大于总体参数，也可能小于总体参数，两者存在误差。因此，由有限的样本资料算出的统计参数，去估计总体的统计参数总会出现一定的误差。这种误差是由于从总体中随机抽取的样本与总体有差异而引起的，与计算误差不同，称为抽样误差。为叙述方便，下面以样本平均数为例说明抽样误差的概念和估算方法。

样本平均数x-是一种随机变量。既然它是一种随机变量，那么就具有一定的概率分布，我们称此分布为样本平均数的抽样分布。抽样分布愈分散表示抽样误差愈大，反之亦然。对某个特定样本的平均数而言，它对总体平均数的离差便是该样本平均数的抽样误差。对于容量相同的各个样本，其平均值的抽样误差当然是不同的。由于是未知的，对某一特定的样本，其样本平均值的抽样误差无法准确求得，只能在概率意义下作出某种估计。样本平均值的抽样误差与其抽样分布密切相关，其大小可以用表征抽样分布离散程度的均方差这个指标来度量。为了着重说明度量的是误差，一般将改称样本平均值的均方误。据中心极限定理，当样本容量较大时，样本平均数的抽样分布趋近于正态分布。这样，便有下列关系：

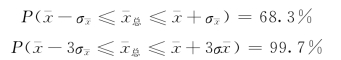(www.daowen.com)

也就是说，如果随机抽取一个样本，以此样本的均值作为总体均值的估计值时，有68.3%的可能性其误差不超过；有99.7%的可能性其误差不超过。

以上对样本平均数抽样误差的讨论，其基本原则完全适用于其他样本参数。抽样误差大小由均方误来衡量，根据数理统计理论，可推导出各参数均方误的公式。计算均方误的公式与总体分布有关，对于皮尔逊Ⅲ型分布且用矩法估算参数时，用分别代表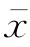、σ、CV和CS样本参数的均方误，则它们的计算公式为：

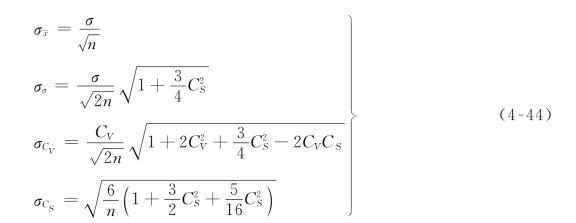
由上述公式可见，样本统计参数的抽样误差随样本均方差σ、离差系数CV及偏态系数Cs的增大而增大；随样本容量n的增大而减小。因此一般来讲，样本系列愈长，抽样误差愈小，样本对总体的代表性就愈好；样本系列愈短，抽样误差愈大，样本对总体的代表性也就愈差。这就是为什么在水文计算中总是想方设法取得较长水文系列的原因。需要指出，上述公式只是表示许多容量相同的样本误差的平均情况，它是不能用来计算某一具体样本的抽样误差的。至于某个具体样本的误差，可能大于这些误差，也可能小于这些误差，实际误差的大小要由样本对总体的代表性高低而定。

可以通过计算验证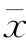，及CV的误差较小，而CS的误差太大，难以应用于实际工作中。经验表明，矩法估算参数，除了有抽样误差外，还具有系统误差（一般小于总体的统计参数值）。因此，在水文分析计算中，通常不直接使用矩法估算参数，而是以矩法公式计算的参数作为初选参数值，然后经过适线来确定。

（2）三点法。皮尔逊Ⅲ型频率曲线具有三个待定的统计参数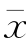、CV和CS。从数学的角度来说，一条曲线的三个未知参数可用任何可能选取的三个条件来建立三个联立方程式，然后解出它们的数值。

首先将经验频率点据绘在频率格纸上，通过点群中心目估一条光滑的经验频率曲线，假定它近似代表皮尔逊Ⅲ型曲线。在该线上任取三点，其坐标为（P1，xP1）、（P2，xP2）和（P3，xP3），对于皮尔逊Ⅲ型曲线，由式（4-33）则得：

其中Φ为P及CS的函数，即Φ=Φ（P，CS）。把所取三点代入上式，可以建立以下三个联立方程式：

解联立方程组（4-45），消去均方差σ，可得：

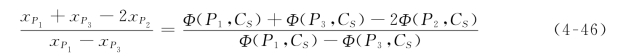
令

称S为偏度系数，当P1、P2、P3已取定时，偏度系数S仅是CS的函数。S与CS的关系已根据离均系数Φ值预先制成，见附表3。当用式（4-47）计算出S后，就可从附表3中查出相应的CS值。统计参数就可用下面的公式计算：

及

其中离均系数φ（P1，CS）-φ（P3，CS）和φ（P2，CS），可从已知的CS查附表4得到，由式（4-48）和式（4-49）可求得σ、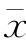，进一步可计算出。

式（4-47）、式（4-48）和式（4-49）就是应用三点法计算参数的基本公式。在实际工作中选取曲线上三个点时，P2一般都取50%；P1和P3则取对称值，即符合P1+P3=100%，例如：取P1=5%，P3=95%；P1=3%，P3=97%或P1=10%，P3=90%等。附表3和附表4中列出了四种P1及P3（P2固定为50%）值的表。如果系列项数n在10左右时，可取P=10%～50%～90%的情况；如果n在20左右时，可取P=5%～50%～95%的情况；如果n在30及100左右时，可分别取P=3%～50%～97%及1%～50%～99%的情况。

【例4-6】资料同[例4-4]，选用某站有代表性的实测年降雨量资料24年，见表4-4中第①、②栏，试用矩法和三点法计算该样本系列的统计参数。

解 矩法的计算过程如下：

1）将系列由大到小重新排列，列入表4-4中第③、④栏。

2）采用式（4-40）计算系列的多年平均降雨量：

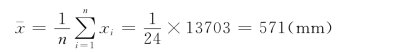
3）计算各项的模比系数，列入表4-4中第⑤栏，其总和应等于n。

4）计算各项的（Ki-1），列入表4-4中第⑥栏，其总和应等于0。

5）计算各项的（Ki-1）2，列入表4-4中第⑦栏，利用式（4-42）可求得变差系数：

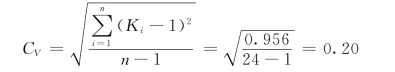
6）计算各项的（Ki-1）3，列入表4-4中第⑧栏，利用式（4-43）可求得偏态系数：

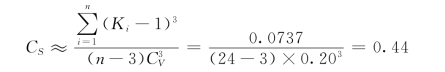
用三点法计算过程如下：

首先按照[例4-4]的方法绘制该站年降雨量的经验频率曲线，如图4-4中虚线所示。从经验频率曲线上读取三点x5%=813mm、x50%=549mm、x95%=368mm，按式（4-47）计算偏度系数S：

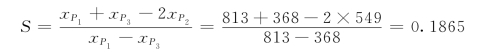
查附表3，当P=5%～50%～95%及S=0.1865时，得：

CS=0.68

再用CS=0.68查附表4得Φ50%=-0.113，Φ5%-Φ95%=3.249，利用式（4-48）和式（4-49），可得：

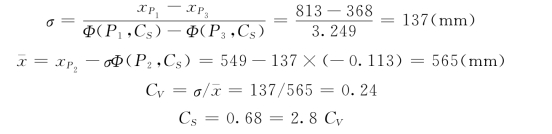
3.统计参数对频率曲线的影响

为了避免适线时调整参数的盲目性，必须了解统计参数对频率曲线的影响。假设水文变量总体服从皮尔逊Ⅲ型分布，现在讨论x-、CV和CS对频率曲线的影响。

（1）均值x-对频率曲线的影响。当皮尔逊Ⅲ型频率曲线的两个参数CV和CS不变时，由于均值x-的不同，可以使频率曲线发生很大的变化，如图4-5所示。由图可见，CV和CS相同时，由于均值不同，频率曲线的位置也就不同，均值大的频率曲线位于值小的频率曲线之上；均值大的频率曲线比均值小的频率曲线陡。

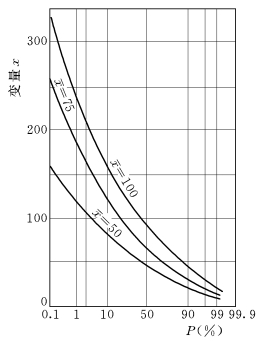
图4-5　均值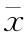对频率曲线的影响

（2）变差系数CV对频率曲线的影响。为了消除均值的影响，以模比系数K为变量绘制频率曲线，如图4-6所示（图中CS=1.0）。CV=0时，说明随机变量的取值都等于均值，此时频率曲线即为K=1的一条水平线。CV越大，说明随机变量相对于均值越离散，因而频率曲线将越偏离K=1的水平线。随着CV的增大，频率曲线的偏离程度也随之增大，曲线显得越来越陡。

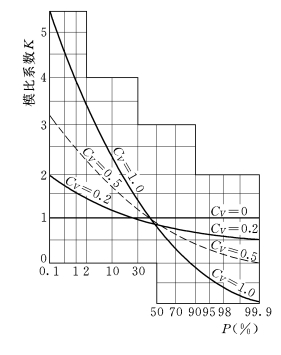
图4-6　变差系数CV对频率曲线的影响

（3）偏态系数CS对频率曲线的影响。偏态系数CS主要影响频率曲线的弯曲程度。图4-7表示CV=0.1时种种不同的CS对频率曲线的影响情况。从图中可以看出，正偏情况下，CS愈大时，均值（即图中K=1）对应的频率愈小，频率曲线的中部愈向左偏，且上段愈陡，下段愈平缓，曲线变弯，即两端部上翘，中间下凹。CS=0时，曲线变成一条直线。

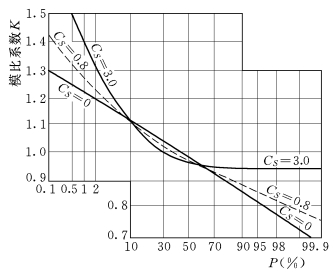
图4-7　偏态系数CS对频率曲线的影响