要掌握随机变量的变化，不仅要关心随机变量可取哪些值，更为重要的是了解各种取值出现的可能性有多大，也就是明确随机变量各种取值的概率，掌握它的统计规律。随机变量可以取所有可能值中的任何一个值，但是取某一可能值的机会是不同的，有的机会大，有的机会小，随机变量的取值与其概率有一定的对应关系。一般将这种对应关系称为概率分布。离散型随机变量的概率分布一般以分布列和分布函数表示；连续型随机变量的概率分布用分布密度和分布函数来表示。

1.离散型随机变量的概率分布

设离散型随机变量用大写字母X表示，它的种种可能取值用相应的小写字母x表示。若取n个，则X=x1，X=x2，…，X=xn。一般将x1，x2，…，xn称为系列，而X可能取值xi出现的概率用pi表示，即

将X可能取值与其相应的概率列成表，称为随机变量X的分布列（表4-2）。由概率的性质可知，任一分布列应满足：

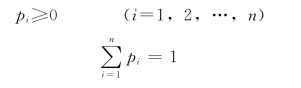
表4-2　离散型随机变量分布列

2.连续型随机变量的概率分布

对连续型随机变量来说，分布列不存在，随机变量可取的值为一连续区间的一切值，无法一一罗列这些值及其概率。比如前面提到的乘客在长途汽车站等车的例子，等车时间可以是0～30min区间里的任何时间，故无法列举所有的随机变量及其相应概率。实际上，等车时间在0～30min的任何时间的可能性是相等的，对于这个区间的任意时间，其概率等于无穷大分之一，即近似等于0。从这个例子可以看出，列举连续型随机变量各个值的概率不仅做不到，而且实际上是没有意义的。

由于连续型随机变量所有可能取值有无限多个，而取任何个别值的概率为零，所以只能研究某个区间取值的概率，或是研究事件X≥x的概率以及事件X≤x的概率，后面二者可以相互转换，在工程水文里面，就是研究某一水文变量大于或等于某一数值的概率。

对于一个随机变量，大于或等于不同数值的概率是不同的。当随机变量取为不同数值时，随机变量大于等于此值的概率也随之而变，即概率是随机变量取值的函数。这一函数称之为随机变量的概率分布函数。分布函数的公式为：

式中 P（X≥x）——随机变量X取值大于或等于x的概率；

F（x）——随机变量X的分布函数。

随机变量的分布函数可用曲线的形式表示。其几何图形如图4-1（b）所示，图中纵坐标表示变量x，横坐标表示概率分布函数值F（x），在数学上称此曲线为随机变量的概率分布曲线。在工程水文里面，又习惯于将水文变量取值大于或等于某一数值的概率称为该变量的频率，同时将表示水文变量分布函数的曲线称为频率曲线。

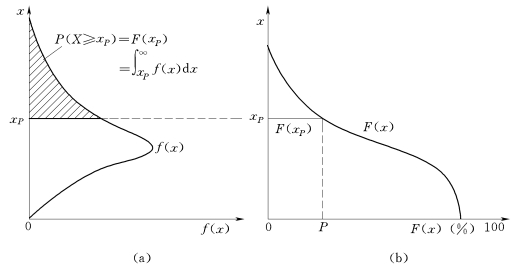
图4-1　随机变量的概率密度曲线和概率分布曲线

（a）概率密度函数；（b）概率分布函数

当研究事件X≤x的概率时，数理统计学中常用分布函数G（x）表示：(www.daowen.com)

称不及制累积概率形式，相应的水文统计用的分布函数F（x）称为超过制累积概率形式，两者之间有如下关系：

对于连续性随机变量，还有另一种表示概率分布的形式——概率密度函数。随机变量概率分布函数的导数的负值，称为概率密度函数，记为f（x），即：

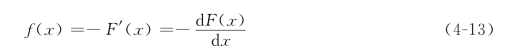
密度函数的几何曲线称密度曲线。水文中习惯以纵坐标表示变量x，横坐标表示概率密度函数值f（x），如图4-1（a）所示。

实际上，分布函数与密度函数是微分与积分的关系。概率密度函数是分布函数的导数。概率密度函数在某一个区间的积分值，表示随机变量在这个区间取值的概率。在工程水文中，频率是水文变量取值大于或等于某一数值的概率，因此，水文变量的频率就是概率密度函数从变量取值到正无穷大区间的积分值。用公式表示，水文变量频率和概率密度函数之间的关系可以写为：

式（4-14）中，F（x）是随机变量X的分布函数值，也就是水文变量X取值为x时的频率，而f（x）是概率密度函数。其对应关系可在图4-1中看出来，图中两边的纵坐标均表示随机变量的取值，图4-1（a）的横坐标表示概率密度函数值，图4-1（b）的横坐标表示频率。图4-1（a）中随机变量取值的概率密度函数值越大，表明随机变量在这个值附近区间取值的概率越大。因频率F（xP）是概率密度函数从xP到正无穷大这个区间的积分，所以，图4-1（b）中的F（xP）等于图4-1（a）中xP以上的阴影面积。从图中可以看到，xP取值越小，阴影面积越大，频率F（xP）取值也越大。这显然是合理的，因为随机变量取值越小，大于等于这个取值的可能性越大。

【例4-3】某水文站具有62年实测年降雨量资料，现按下列步骤进行统计分析。

解 1）将年降雨量分组，并统计各组出现次数和累积次数。分组距离Δx=200mm，统计结果列于表4-3中的①、②、③、④栏。第④栏为累积次数，表示年降雨量大于或等于该组下限值x的出现次数。

2）计算各组出现的频率、累积频率及组内平均频率密度。将表4-3中的第③、④栏数值除以总次数62，即得⑤、⑥栏中的相应频率；将第⑤栏中的组内频率ΔP除以分组距离Δx得第⑦栏中数值，它表示频率沿x轴上各组所分布的密集程度。

表4-3　某站年降雨量分组频率计算表

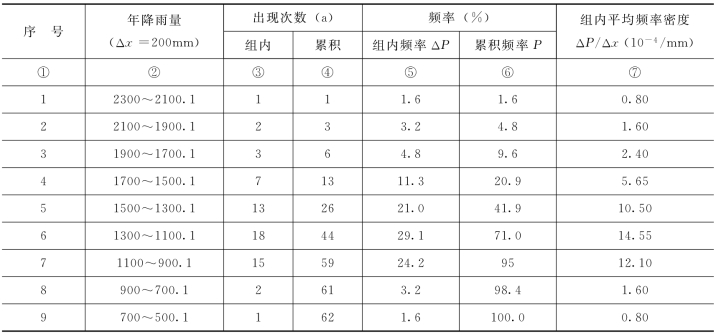
3）绘图。以各组平均频率密度ΔP/Δx为横坐标，以年降雨量x为纵坐标，由表4-3中的第②、⑦栏数值，按组绘成直方图，如图4-2（a）实线所示。各个长方形面积表示各组的频率，所有长方形面积之和等于1。这种频率密度随随机变量取值x变化的图形，称为频率密度图。频率密度值的分布情况，一般是沿纵轴x数值的中间区段大，而上下两端逐渐减小。如果资料年数无限增多，分组组距无限缩小，频率密度直方图就会变成光滑的连续曲线，频率趋于概率，则称为随机变量的概率密度曲线，如图4-2（a）中虚线所示。

以累积P为横坐标，以年降雨量x为纵坐标，由表4-3中的第②、⑥栏数值，按组绘成如图4-2（b）所示的阶梯形实折线。这种表示大于或等于x的累积频率随随机变量取值x变化的图形，称为频率分布图。同样，如果资料年数无限增多，分组组距无限缩小，实折线就会变成S形的光滑连续曲线，频率趋于概率，则称为随机变量的概率分布曲线，如图4-2（b）中虚线所示。

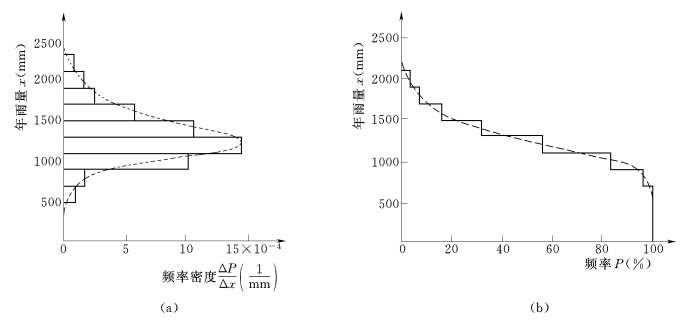
图4-2　某站年降雨量频率密度图和频率分布图

（a）频率密度图；（b）频率分布图

概率密度曲线和概率分布曲线从不同的角度描述了水文变量的概率分布规律。从年降雨量的分布规律中可知，特别大或特别小的年降雨量出现的机会较少，而中等大小的年降雨量出现的机会较多。其他水文要素，如年径流量等，也都具有这种特性。在水文计算中，一般不绘制水文变量的概率密度曲线，而绘制其概率分布曲线。水文统计上习惯把概率分布曲线称为频率曲线。