齿轮与轴承等零件在工作中，均承受着较大的接触应力。如果材料的强度不足，则会在接触处发生接触疲劳破坏。为了对接触疲劳破坏的原因进行分析并提出预防措施，对接触区附近的应力场及其特点应掌握以下几点。

1.接触面间的赫兹应力

两物体接触表面附近的应力场理论是根据赫兹（Hertz）的弹性理论提出的。该理论认为，接触表面的接触应力按椭圆规律分布，其中心达最大值。两平行圆柱体相互接触时的应力分布如图2-36所示。

如图2-36所示，半径分别为R₁和R₂的两个平行圆柱体相接触时，当其上受到法向力P_N的作用后，由于弹性变形，在接触处将发生宽度为2b的接触带（或变形带）。接触带的半宽度b的计算式为

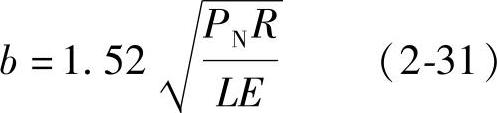
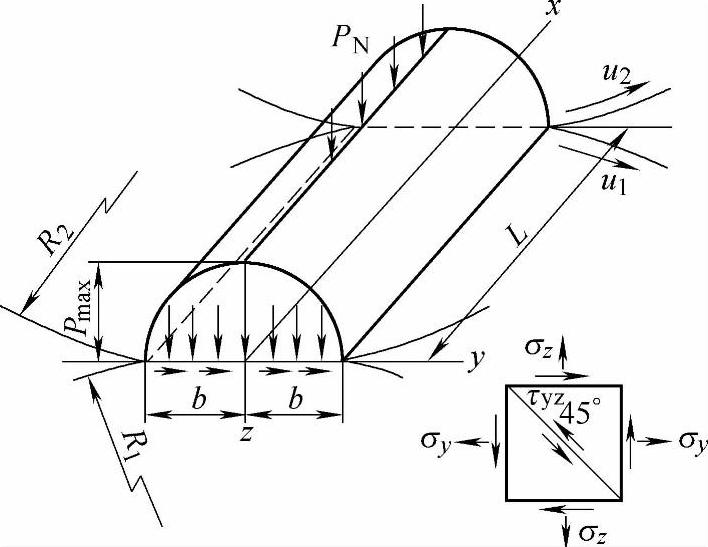
图2-36 两平行圆柱体相互接触时的应力分布

接触压应力在2b上的分布为半椭圆形，最大接触应力在接触面的中心，称为赫兹应力，其值为

式中 σ_j——赫兹应力；

P_N——接触带长度上的法向力；

R——两个圆柱体的当量曲率半径；

E——当量弹性模量；

L——圆柱体的长度。

2.沿圆柱体接触面的对称平面（y=0）上各点的应力分量

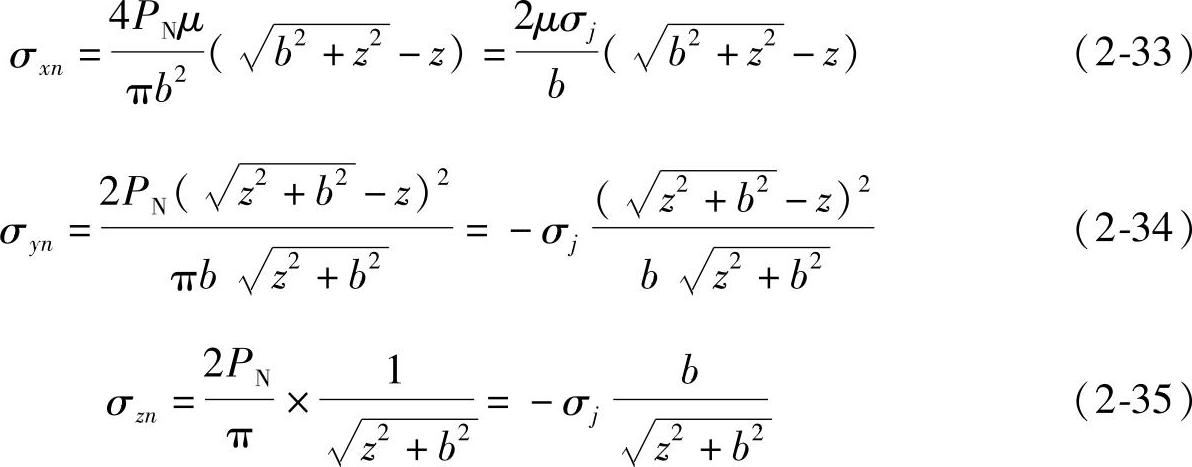(www.daowen.com)

式中 μ——泊松比，对于钢，μ=0.25～0.33，对于渗碳层，μ≈0.28；

z——距接触面的深度。

由此可知，随z值的加大，各应力分量均降低。

3.最大切应力

数值计算式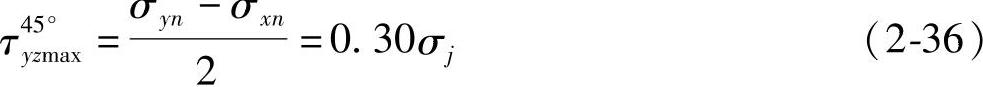

所在位置

即切应力τ_yz（45°）在z=0.786b处达最大值。

4.交变切应力

实际运转的轴或齿轮，其接触点是不断变化的，因此，对零件上某一固定点而言，各应力分量也是周期变化的。在只考虑法向力的情况下，交变切应力τ_yzn的最大值在z₀=0.5b处，其值τ_yznmax=0.25σ_j。

5.摩擦力对接触应力的影响

大多数的滚动元件是在滚动兼有滑动的条件下进行工作的。由于塑性变形引起附加应力，完全纯滚动的情况是极少见的，因此，在接触面间，除了接触应力外，尚存在摩擦力的作用，表面摩擦力对接触区的应力场将产生影响。表面粗糙度值较大时将使最大综合切应力移向表面，当摩擦因数为1/3时，最大主应力分量将增加39%；最大切应力分量将增加43%；最大交变应力分量将增加36%；最大切应力所在位置，由距表面0.786b处，移至表面，并向y方向偏离0.3b。

实验分析表明，当摩擦因数大于1/9时，最大切应力已移至表面。对微合金化细片状珠光体钢钢轨钢PD3钢研究表明，光滑表面的试样的裂纹萌生位置与τ^45°_yzmax和τ_0max所在的位置基本相符；表面粗糙度值较大时，裂纹在表面萌生。

裂纹萌生位置越深，扩展倾角越小，裂纹从亚表面扩展到表面所要经历的路径就越长，在相同的扩展速率下，产生剥落所需的循环次数就越多，接触疲劳寿命则越高。

在分析接触疲劳裂纹的萌生位置时，应力场的这一变化应当注意。