在生产实际中，受拉（压）应力的零件是多种多样的，如连杆、螺栓、钢丝绳等。

1.评定单向应力的指标

（1）数学表达式评定单向应力的数学表达式如下：

对于脆性材料

对于塑性材料

式中 [σ]——许用应力；

σ₀——危险应力，对于脆性材料，σ₀=R_m，对于塑性材料，σ₀=R_eL；

n——强度储备系数，又称安全系数；

n_m——以抗拉强度为基础的安全系数；

n_e——以屈服强度为基础的安全系数。

（2）许用应力 所谓许用应力就是允许达到的应力。其创始人是巴哈（C.V.Back）。对机械零件最基本的要求就是具备足够的强度，为了保证零件在外力作用下，能够安全可靠地工作，应使它的工作应力低于材料的承受能力，使零件的强度留有必要的储备。因此，常把材料的强度指标除以大于1的系数n，作为设计时应力的最高限度，称为许用应力，用[σ]表示。

静载情况下，拉伸和压缩时常用材料的许用应力[σ]见表2-6。

表2-6 拉伸和压缩时常用材料的许用应力[σ]

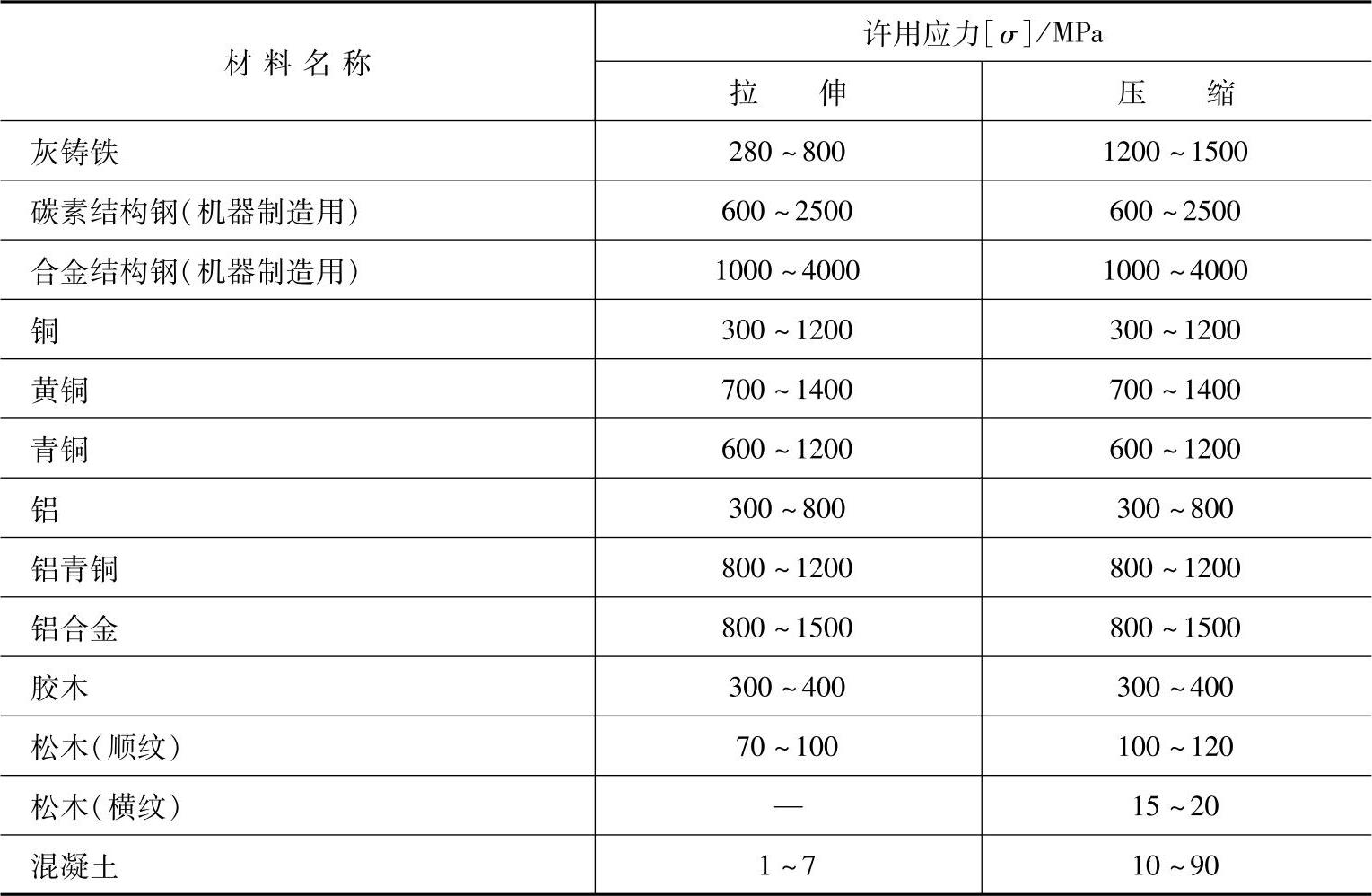
（3）安全系数及影响安全系数的因素

1）安全系数是一个大于1的数值。工程上使用的安全系数一般如下：

①对于重型机械，n=3.5～4.0。

②对于一般机械（承受静载时），n_e=1.5～2.0，n_m=2.0～5.0。

③对于万吨轮轴系，n_e=2.5～5.5。

④对于起重设备中的吊钩，n=5。

2）影响安全系数的因素很多，主要有以下几点：

①材料化学成分的波动及冶金缺陷。

②加工制造过程中带来的损伤、热处理缺陷（如氧化、脱碳、组织不合格、残余应力等）。

③使用过程中的负荷偏差（瞬时过载）。

因此，并不是说设计时取的安全系数越大，设备就越安全。材料的许用应力值一般是按照材料试验的平均性能或统计数据提供的。当材料或加工因素导致材料性能发生较大的波动时，其安全可靠性就发生变化，有些过载断裂失效就是由此引起的。因此，在分析断裂问题时，不能简单地校核安全系数或许用应力大小。

2.提高材料强韧性能的措施(www.daowen.com)

为了充分发挥材料的潜力，提高材料的许用应力，使零件安全可靠地服役，其基本出发点是如何提高材料的强韧性能，在生产实践中采取的主要措施有：

1）零件承受拉应力，并且在整个截面上的分布是均匀的，此时，在选材和确定热处理工艺时，应当根据零件的截面大小，确保零件内部完全淬透。

2）零件承受弯曲、扭转或弯扭复合应力，如一般的轴类零件、齿轮类零件，为了保证零件具有足够的硬度和强度，同时又具有高的韧性，在选材和热处理时应保证一定厚度的淬硬层，而保留心部较高的韧性，如一般轴类零件要求其淬硬层为轴半径的1/3～1/2。

3）防止氧化、脱碳、过热、过烧等一切降低材料性能的缺陷发生。

3.失效分析

此类零件的断裂应首先区分是韧性断裂还是脆性断裂。

（1）韧性断裂 对于韧性断裂，应分析以下方面：

1）首先按传统的强度理论进行强度校核，检查一下载荷是否估计不足，即安全系数是否太小或者未予以考虑。

2）分析材料的组织状态，检查硬度，检查是否有氧化脱碳、淬火裂纹，以及心部是否淬硬等。

3）如果上述问题不存在，应做化学成分分析。

（2）脆性断裂 除做上述考虑外，尚须进行断裂韧度检查，主要分析微观裂纹的存在对韧性的影响。

例 国产45Si2Mn高强度螺栓，在加工制造过程中，不可避免地存在着深为a=0.5mm，半宽c=2.0mm的表面裂纹，其工作应力为σ=960MPa。淬火并低温回火后材料的抗拉强度R_m=2110MPa，下屈服强度R_eL=1920MPa，K_IC=39.50MPa.m^½，在使用中发生脆断，试分析原因。

分析一 按传统强度理论校核如下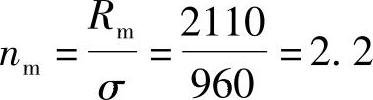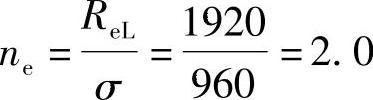：，，应是安全的。

分析二 因为是高强度材料，还应进行断裂力学方面的校核。作为近似计算，该裂纹认为是一个张开型的表面裂纹，其应力强度因子按式（2-9）计算，在临界条件下，式（2-9）可写成

式中 σ_c——垂直于裂纹所在平面的最大拉应力。

由式（2-19）可得

根据裂纹形状和应力状态，查有关手册后可得与此有关的裂纹形状因子数据，将有关数据代入后得σ_c=948.5MPa。

由此可见，零件最大承载能力为948.5MPa，低于实际的工作应力960MPa，故发生断裂失效，又因其断裂时的应力小于材料的屈服强度，所以必然是脆性断裂。

若将淬火并低温回火处理改为调质处理（淬火并高温回火），则得R_m=1540MPa，R_eL=1440MPa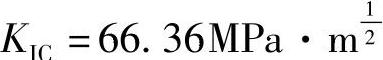，，其结果为

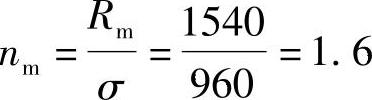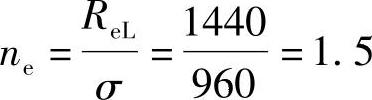，，也是安全的。

同样，在有裂纹存在情况下，由断裂韧度求得σ_c=1564.5MPa＞σ（工作应力，960MPa）。

上述情况表明，减小强度的安全系数，即降低材料的R_eL和R_m值，零件的安全性能反而提高了，这是传统的强度理论无法解释的。也就是说，在具有脆性断裂倾向的零件中，决定零件断裂与否的关键因素是材料的韧性，而不是传统的强度指标，片面地追求高强度和较大的强度安全系数，往往导致韧性的降低，反而容易促使宏观脆性的、危险的低应力断裂。因此，在强度设计、材料选择及制订热处理工艺时，应以韧性为主，并全面考虑材料的常规力学性能指标，使强度和韧性具有良好的配合，才能确保零件的安全使用。

在上述例子中，将原来的淬火并低温回火处理，改为调质处理（淬火并高温回火）后，允许的工作应力由原来的948.5MPa提高到1564.5MPa，且这一指标大于材料的下屈服强度R_eL=1440MPa。这表明，该零件如果由于其他原因而发生断裂，也将是宏观塑性的，其危险性较小。