零件的应力状态分析和力的计算，是力学和机械设计学的主要研究内容，这里只对涉及零件失效的几个主要问题进行简要讨论，详细的理论分析和计算请参阅有关专著。

1.材料的失效形式和应力状态

应用应力状态的概念，可以分析材料破坏的原因。

材料的失效形式大致可分为三种：

1）脆断：断裂前无宏观塑性变形，例如铸铁拉伸、扭转时，几乎没有塑性变形就被拉断。

2）剪断：沿最大剪应力方向发生的断裂，例如铸铁在压缩和硬铝在拉伸时，大约沿45°方向剪断。

3）屈服：经过一定的塑性变形后才发生的断裂，例如低碳钢拉伸、扭转和压缩时，都有很大的塑性变形。

不同的材料在受力相同的情况下可能出现不同的失效形式，塑性材料一般会出现塑性变形，而脆性材料一般会出现脆性断裂。同一种材料在不同的受力状况下也会有不同的失效形式，这一点在失效分析中应引起足够重视。例如铸铁，在拉伸、扭转时都是脆断，但受压时却表现出一定的塑性。光滑试样与缺口试样的拉伸行为也各不相同。可见材料的失效形式不是一成不变的，但这个变化是有条件的，即应力状态的变化或影响，另外还有温度、加载速率等也起作用。

一般来说，在受力零件的同一截面上，不同点的应力并不相同；而且在通过同一点的不同截面上，应力的大小和方向也随截面的方向不同而变化。在零件上的任一点的三个主应力中只有一个不为零，称为单向应力状态，两个或三个主应力不为零，则称为二向和三向应力状态。

图2-32所示为圆轴扭转时的应力状态及铸铁试样受扭时的断裂现象。圆轴在扭转时，在横截面的边缘处切应力最大，其数值为

在圆轴的最外层，按图2-32a所示方式取出单元体ABCD，单元体各面上的应力如图2-32b所示。在这种情况下，σ_x=σ_y=0，τ_x=τ，这就是纯切应力状态。可求出纯切应力状态的主应力为

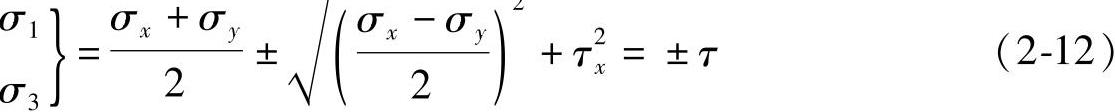
在这里，σ₂=0。这是一个二应力状态，两个主应力的方向（主平面）与圆轴的轴向呈45°（见图2-32b）。铸铁试样扭转时，表面各点的主平面（主应力）连成倾角为45°的螺旋面。由于铸铁抗拉强度很低，试样将沿这一螺旋面因拉伸而发生断裂破坏，如图2-32c所示。脆性材料扭转时的断裂形式与此类似。

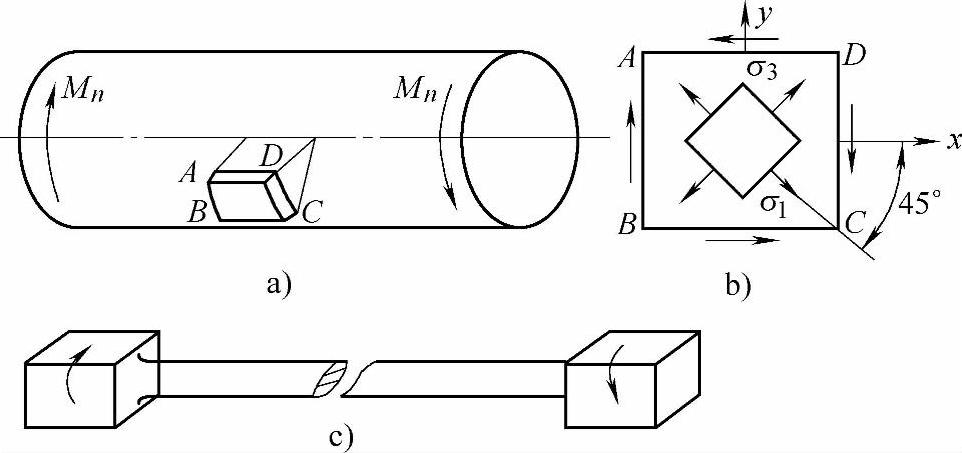
图2-32 圆轴扭转时的应力状态及铸铁试样受扭时的断裂现象(www.daowen.com)

2.强度理论

材料在不同的应力状态下表现出不同的失效形式，这与材料在对应状态下表现出来的抗力有关。在工程实际中，大多数受力零件的危险点都处于复杂应力状态下。显然，在复杂应力状态下，不能再仿照在简单应力状态下的试验方法来确定强度条件。对于在不同的应力状态下如何表示材料的抗力，人们提出了种种假说，推测材料在复杂受力状态下破坏的原因，这就是强度理论，常见的有五种，见表2-5。

表2-5 强度理论及其应用范围

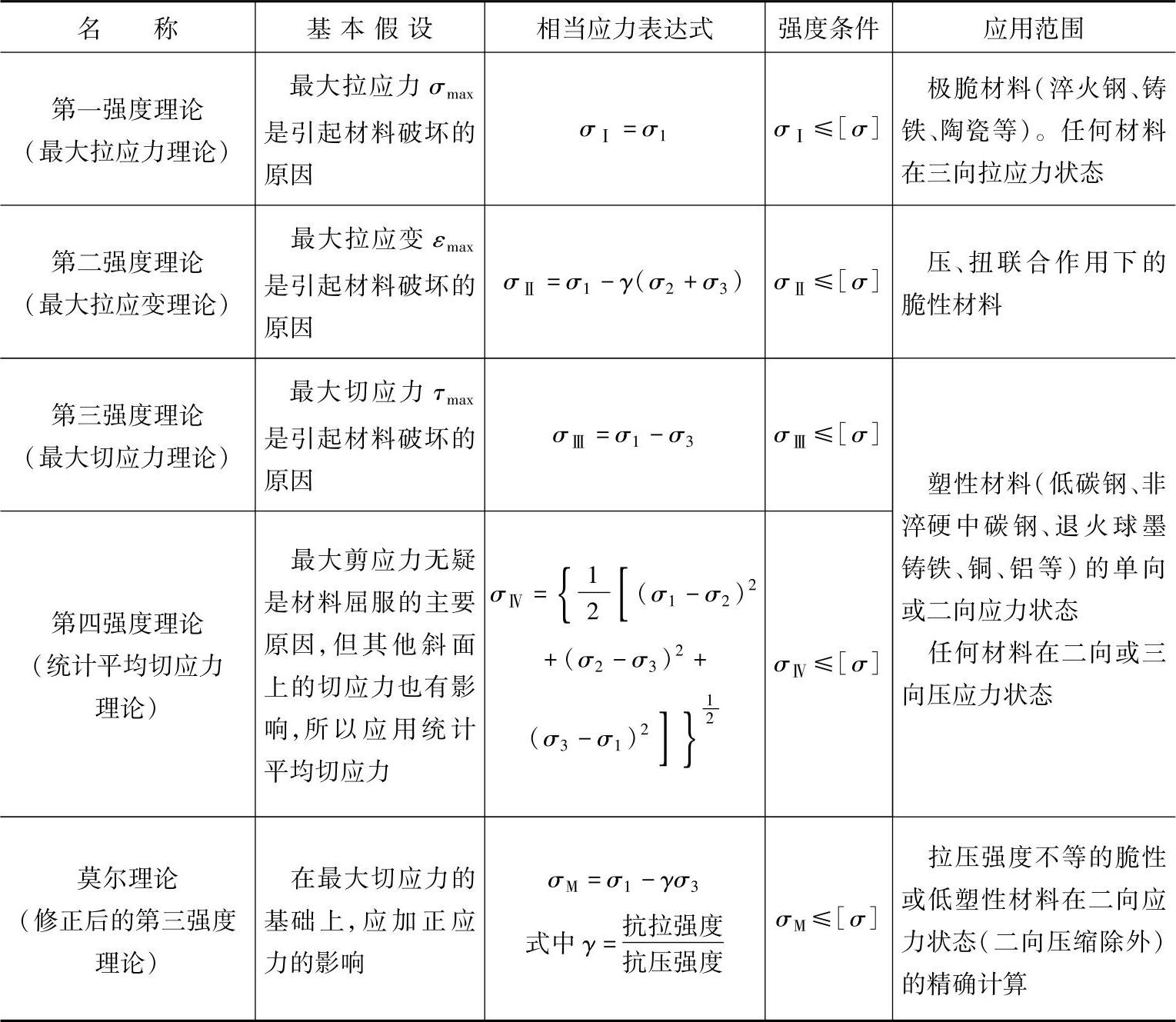
有了这些理论，便可根据简单试验（如拉伸试验）所测得的材料抗力，分析计算其他复杂应力状态下材料的强度。如按强度理论可以建立纯切应力状态的强度条件，并可以由此确立塑性材料许用剪应力[τ]与许用拉应力[σ]之间的关系。

如前所述，纯切应力状态是一拉一压二向应力状态，且σ₁=τ，σ₂=0，σ₃=-τ。对塑性材料应采用第三或第四强度理论。按第三强度理论得出的强度条件为。

另一方面，剪切的强度条件为

比较式（2-13）和式（2-14），可得

按第四强度理论可得

对于同一种材料，采用不同的强度理论进行分析，有时会得出不同的结果。如铸铁在二向拉伸一向压缩且压力较大的情况下，试验结果与按第二强度理论的计算结果相近；而按照这一理论，铸铁在二向拉伸时应比单向拉伸安全，这显然与试验结果不相符，在这种情况下用第一理论计算的结果就比较接近试验数据。因此，在进行实际分析时应按表2-2给出的各种强度理论的适用范围选用。