零件截面有急剧变化处，就会引起局部地区的应力高于受力体的平均应力，这一现象称为应力集中，表示应力集中程度大小的系数称为应力集中系数。图2-2表示一受力为P、截面面积为A的无限宽板上有椭圆孔后的应力分布情况。平均应力为σ_m=P/A，在椭圆孔长轴两端出现应力集中。此时，应力集中系数为

椭圆孔长轴顶端的曲率半径为ρ，大多数情况下，a＞＞ρ，由此式（2-1）也可写为

若图2-2中的椭圆孔的b趋于零，则该孔口退化为x方向、长度为2a的裂隙。如图2-3所示。当零件承受图示的应力状态时，裂隙端点附近的应力分布为

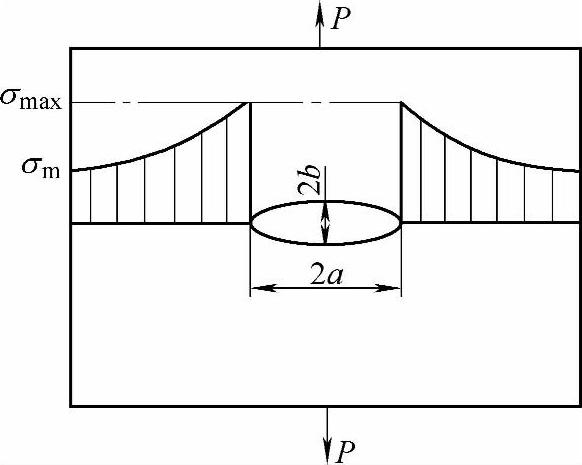
图2-2 应力集中示意图

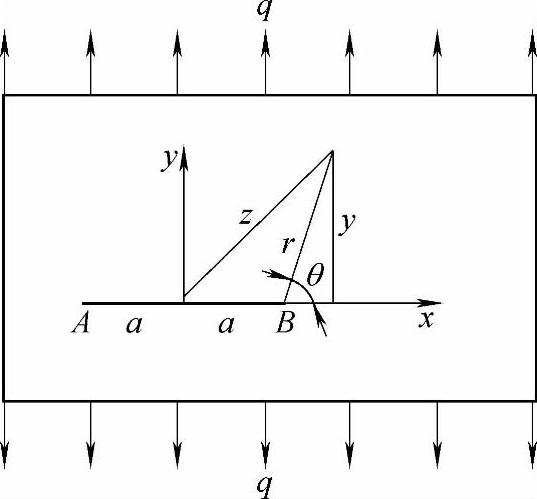
图2-3 裂隙附近的应力集中

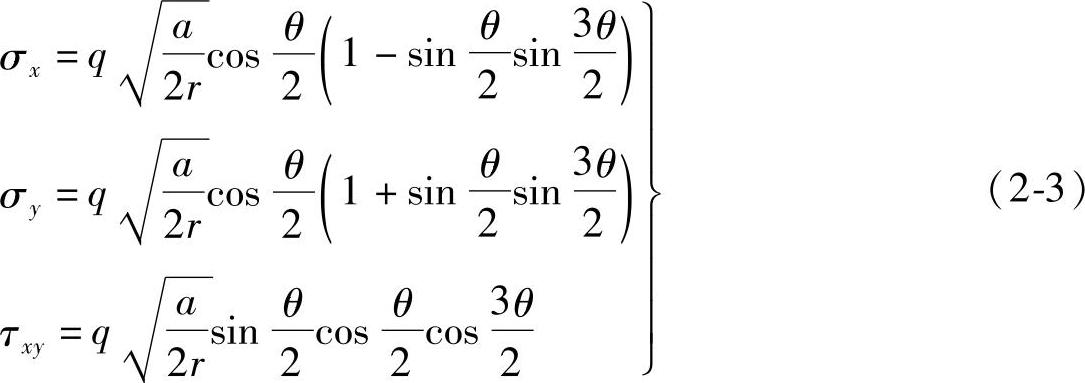
式中σ_x、σ_y——沿x、y方向的正应力；

τ_xy——作用在y面上沿x方向的切应力。

当薄板或长柱在裂隙方向及其垂直方向受有均布剪力q时，其裂隙端点（裂隙形式和图2-3相同）附近的应力分布为(www.daowen.com)

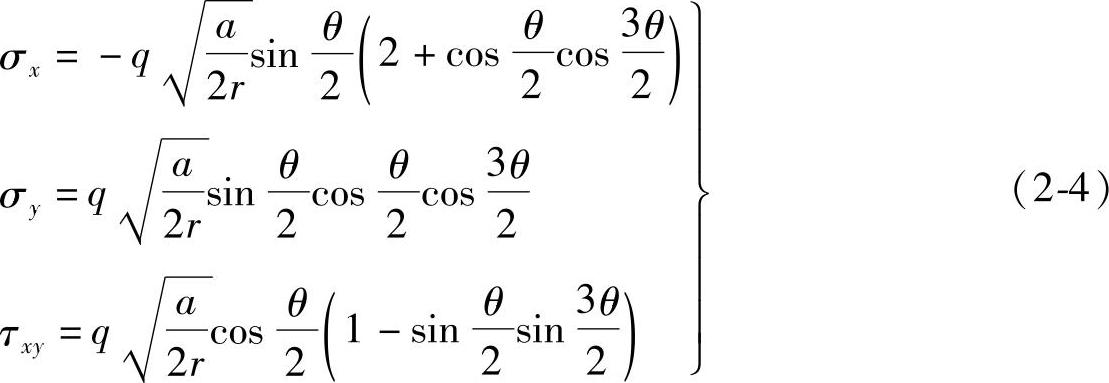
如果在式（2-3）或式（2-4）中令r趋于零，则各个应力分量的数值趋于无限大。这就表示，在裂隙的端点，应力是无限大的。上述应力集中现象及应力集中系数的计算是在弹性力学基础上确定的。当最大应力超过材料的屈服强度（或满足屈服条件）就要发生局部塑性变形，此时就有可能起应力松弛作用，就不会发生无限大的应力。所以上述的应力集中系数也称为理论应力集中系数。虽然如此，对于脆性材料，以及在塑性区范围很小的情况下，上述描述可以令人满意地表明裂隙附近的应力状态。

应力集中的程度首先是与缺口的形状有关。一般来说，圆孔孔边的应力集中程度最低。因此，如果有必要在零件上挖孔或留孔，应当尽可能地用圆孔代替其他形状的孔，至少应采用椭圆孔，以代替具有尖角的孔。

影响应力集中系数的因素还有很多，如零件结构，缺口位置、大小，材料种类，载荷性质等，具体情况应具体分析。表2-2列出部分试样的应力集中系数。图2-4所示为常见典型结构的应力集中曲线，详细的数据可查阅相关技术手册。

表2-2 部分试样的应力集中系数

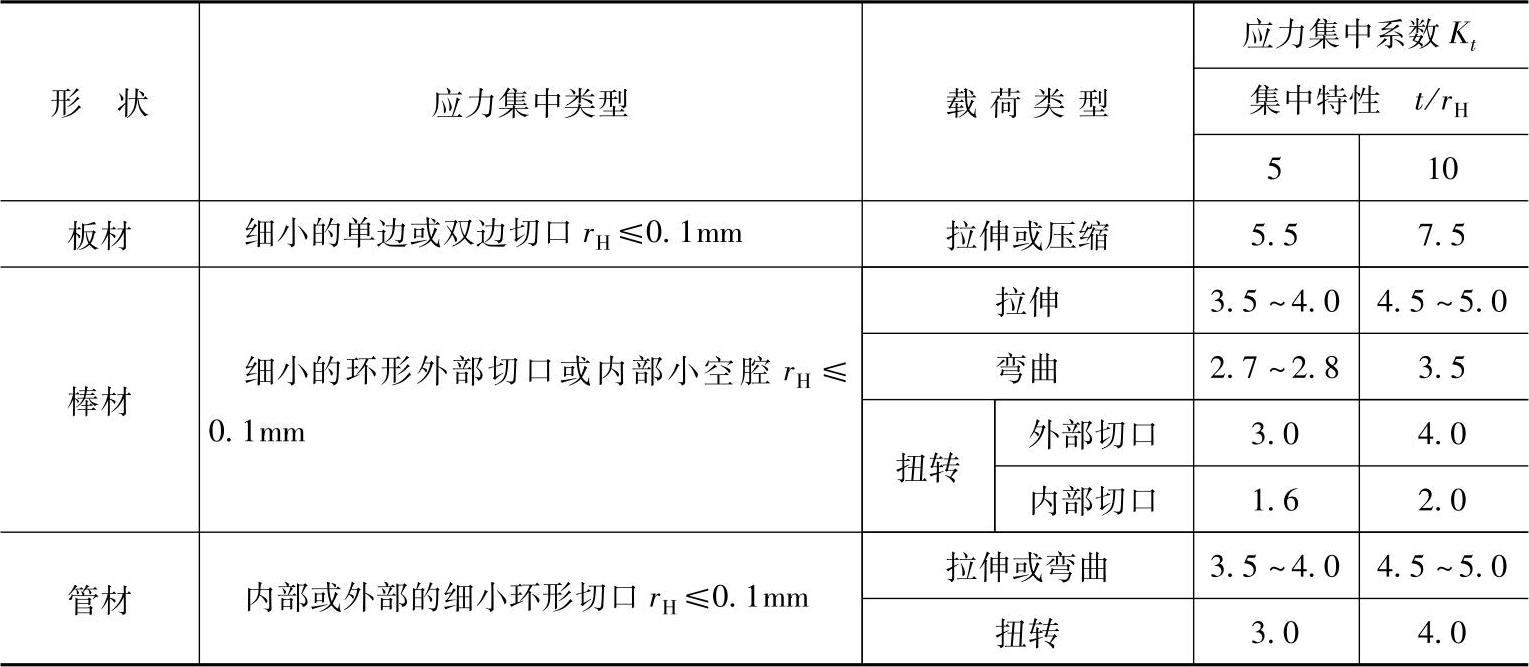
注：t—切口深度；r_H—切口尖端半径。

在机械零件发生疲劳破坏时，如对一个缺口零件考虑应力集中时，则缺口件的疲劳强度应按应力集中系数的倍数降下来。但实验表明这样处理有些过于保守。因此，工程中一般采用有效应力集中系数K_f来进行计算。

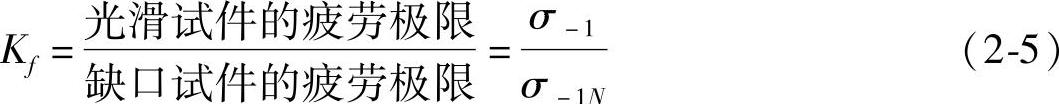
K_f的大小与材料的缺口敏感程度及缺口根部情况有关，详见第5章。

有时，在零件的一种应力集中源上又叠加了另一种形式的应力集中源，如在缺口上刻有划痕，此时的应力集中程度应用复合理论应力集中系数(K_t)_复合来表示：