6.4.2.1　完备性

给定一个安全参数n,为了IBE的完备性成立,我们需要:

1.Setup算法能够正常工作要求陷门抽样算法能够确保成立.因此令

2.Extract算法正常工作要求确保PSF 算法成立.令

3.加密算法能正常工作需要的参数限制条件如Gentry的对偶加密方案一致[38].为此我们需要令

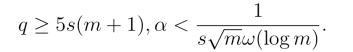
4.除以上要求外,我们还需要确保抽取自分布Ds/(l+1),o的l + 1个高斯向量{vi} 满足Avi(modq) 应接近均匀分布,且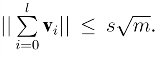因此应保证高斯向量抽取时高斯参数s/(l+1)应大于光滑参数.即

其中为此,设s=6(l+1)ω(log n).

综上,参数(m,q,s,α)设置如下:

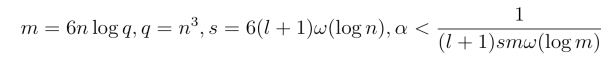
其中l ＜n 为身份信息的长度.

显然,基于以上参数,所提方案的完备性成立.

6.4.2.2　安全性

方案的安全性证明中需要如下引理[43].

引理6.2 令Λ 是一个格,σ ∈R.对i = 1,2,··· ,k,令ti ∈Zm 和xi 为相互独立的抽取自ti +Λ上的高斯分布,Dti+Λ,σ.令c = (c1,··· ,ck) ∈Zk,定义g = gcd(c1,··· ,ck),假设σ ＞‖c‖η∈(Λ)对某∈成立,其中η∈(Λ)为格Λ的光滑参数.则统计接近Dt+gΛ,‖c‖σ.

该引理说明离散高斯分布的线性组合依然服从离散高斯分布.不仅如此,组合函数的高斯分布仅仅依赖于(g,c,t,Λ).

定理6.2 假设Gentry的对偶加密方案是语义安全的,LWE问题在本方案所取参数下是困难的,则本节设计的IBE方案满足标准模型下的IND-aID-CPA 安全性.

证明: 我们使用如下四个Games来证明方案的安全性是基于LWE问题的困难性.其中第一个Game是标准的IND-aID-CPA 定义中的Game.而最后一个Game被任何敌手看来都是完全随机的.我们证明在LWE问题的困难性假设下,给定的四个Game对任何PPT的区分器而言是不可区分的.从而,任何敌手在标准IND-aID-CPA Game的优势是可忽略的.

Game 1.该Game是标准的IND-aID-CPA game.

Game 2.该Game将Game 1中的公钥向量ci,i=0,1,··· ,l,的生成修订为如下方式,

Step 1.挑战者首先依照高斯分布Ds/(l+1),o生成l+1 小向量vi.

Step 2.挑战者计算Avi(modq)=ci.

Step 3.验证ci 线性无关,否则返回step 1.

Game 2的其他部分同Game 1一致.

Game 3.该Game与Game 2一致,除了矩阵A是随机均匀选择的.

Game 4.该Game与Game 3一致,除了挑战密文被取代为相同长度的随机数组.

以下结论说明以上Game分别是不可区分的.(www.daowen.com)

结论1.Game 1 和Game 2 不可区分.

证明: 因为s/(l+1) = cω(log n) ≥ηε(Λ⊥q(A)),而vi 是依照Ds/(l+1),o分布抽取的,所以Avi(modq)=ci 的分布与均匀分布的统计距离不超过2ε.结论1 得证.□

结论2.Game 2 和Game 3 是不可区分的.

证明: 为了证明结论2,我们只要证明挑战者在Game 3中依然可以如Game 2中一样模拟完成提取询问.在Game 3中,挑战者计算

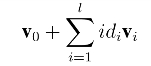
对关于身份id = (id1,id2,··· ,idl) ∈{0,1}l的密钥提取询问的回答,因为所有的vi,i=0,1,··· ,l 都服从Ds/(l+1),o分布,则v0+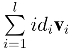服从的分布统计接近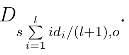另一方面,

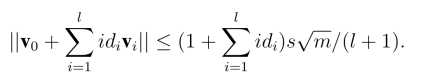
因此,对敌手而言,向量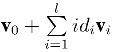与身份id=(id1,id2,··· ,idl)∈{0,1}l的真正私钥是不可区分的.结论得证□

结论3.Game 3 和Game 4 是不可区分的.

证明: .假如存在敌手能够以不可忽略的概率区分Game 3 和Game 4,则我们可以构造一个挑战者接近判定型LWE问题.假设挑战者收到一个LWE实例挑战者希望确定(A,y)是一个LWE 实例或者是一个随机实例.挑战者与敌手执行如下游戏.

1.Setup.挑战者选择l+1 短向量vi 服从高斯分布Ds/(l+1),o,并计算l+1 线性独立向量Avi(modq)=ci.族公钥为(A,c0,··· ,cl).

2.Extract 1.敌手适应性询问身份{ID1,··· ,IDλ}的私钥.给定身份IDi =(idi1,··· ,idil),挑战者计算

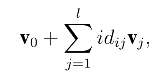
作为身份IDi 的公钥.

3.Challenge.当敌手决定结束第一阶段的提取询问,敌手随机选择两个消息M0,M1 ∈{0,1}.敌手选择一个挑战身份ID* = (id*1,··· ,id*l) 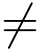IDi,i = 1,2,··· ,λ 作为攻击目标.挑战者选择一个随机比特b ∈{0,1},计算挑战密文

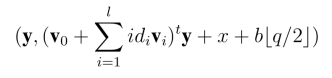
表6.3　效率比较

其中x 服从Φα分布.

4.Extract queries 2.敌手继续适应性对ID 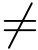ID*的身份询问其对应私钥,挑战者则如第一阶段的密钥提取询问一样,对这些询问做出应答.

5.猜测.最后,敌手完成对Game 3 或者Game 4 的猜测.假如敌手认为在执行Game 3,则挑战者确定(A,y)是一个LWE 实例,若不然,(A,y)是随机均匀的.

6.分析.显然,假如(A,y)是随机的,挑战密文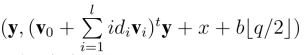是随机的.假如(A,y)是一个LWE问题实例,则模拟密文为“真实”的:

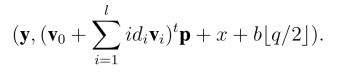
事实上,

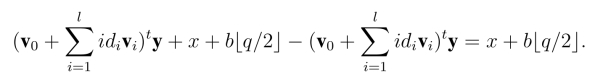
从而,假如低手能够以优势ε区分Game 3 和Game 4,则挑战者C 能够以相同的优势区分LWE问题实例和相应的随机实例.□

将以上四个结论联立可知,任何PPT 敌手赢得标准IND-aID-CPA 游戏的的优势是可忽略的.从而定理得证.□

6.4.2.3　效率分析

将本节方案与已有的格基(H)IBE 方案比较,得到表6.3.在表6.3中,参数d 为分级深度,而l 是身份信息的长度.因为本节提出的方案不是分级的,我们令已有的HIBE中令d = 1.为了便于比较,假设所有方案选取相同的安全参数n.则由表6.3知,本节所提方案的公钥尺寸短于已有的格基IBE方案.