6.3.4.1　选择参数及完备性

给定安全参数n,为了方案正确执行,我们需要满足如下条件:

1.陷门抽样算法确保执行以保证系统建立算法运行正确,为此,设:

2.固定维数的格基代理算法应确保执行,为此,令

因此

3.基于LWE问题的陷门单向函数确保解密成功,以保证第l 层解密正常.为此,设

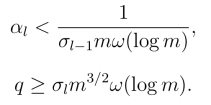
令d 为最大分级深度.为了满足上面的需求,取如下参数(m,q,σ,α):

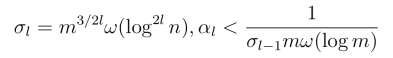
显然,给定以上参数,PKG能够为1层用户提取私钥.而l层用户也可以为k层用户(l ≤k ≤d)提取私钥.显然解密算法能够正常运行.

方案的完备性可证.

6.3.4.2　安全性

定理6.1 假如判定型LWE问题在错误分布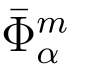是困难的,所提的HIBE方案在选择身份-选择明文攻击下是安全的.

证明: 假设存在一个敌手能够在选择身份选择明文攻击下获得优势∈.则我们首先构造一个区分器D 以至少∈/2 的优势区分分布

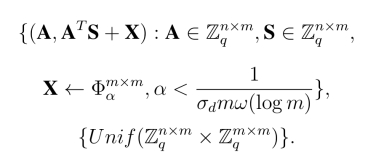
一个选择身份模型下的敌手首先输出挑战身份 假设挑战身份的汉明重量为k*,即

D 收到一个来自两个挑战分布的挑战实例(A0,B).于是D 准备敌手A的模拟攻击环境如下.

1.随机抽取k*矩阵Rj1,··· ,Rjk* 服从分布Dm×m.令

对每一个i=jl ∈{j1,j2,··· ,jk*},令Ri =Rjl.

2.若i /∈{j1,j2,··· ,jk*} 且i ≤d,通过陷门抽样算法生成于是AiTi =0(modq)且‖Ti‖≤O(n log q).

3.通过运行PSF至多m2次生成R′i,(www.daowen.com)

其中ji* ∈{j1,j2,··· ,jk*}是第一个大于i的数.所以AiR′i =A0Rjk*···Rji*(modq),‖R′i‖≤

令Ri =R′i,其中i /∈{j1,j2,··· ,jk*},i ≤d.

4.发送{A,R1,R2,··· ,Rd}给敌手A(其他参数如方案所示).

密钥询问.A 执行身份id|l的密钥提取询问,其中id|l不是id*的前缀.

设|id| = l ≤d.为了表述简便,假设l = d (当l ＜d 时,类似可得).因为id|l 接近随机且不是id* 的前缀,并存在第一个位置i0 满足idi0 = 1,id*i0 = 0.又因为区分器D 拥有格的陷门基Ti,所以,D 可以回复关于身份id|l的密钥询问如下:

1.如加密算法表示的那样,选择矩阵Rij,idij = 1,ij ＞i0 .假设矩阵Rij的数目是j′.从而身份id|l的公钥矩阵为

2.生成格的陷门基Tid|l.令A′ =Fid|lRij′···Ri1,

Challenge.A 输出一个挑战消息则对一个随机比特b ∈{0,1},D 返回M0+2B(log q)作为挑战密文.

Phase 2: A 可以执行更多的密钥提取询问,而区分器的回答如Phase 1所示.

Guess.最后,A 输出一个猜测比特.D 输出1,假如A 猜对比特b,若不然,输出0.

则我们可以分析区分器D 的优势如下.假如B 是一个均匀随机矩阵,M0+2B(log q)依然是一个均匀随机矩阵.所以D 将以概率1/2输出1.若B = 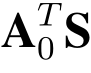+X(modq),挑战密文 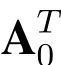S′+2X+M(modq)的分布与加密算法输出的密文分布一致,其中S′ =2S 是服从均匀分布.从而,D 以概率(1+∈)/2输出1.

综上,区分器的优势是∈/2.

显然区分器可以被用于解决带错误分布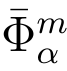 的判定型LWE问题.□

6.3.4.3　效率分析

与文献[42]的方案比较,本节方案的最大优势在于公钥尺寸被有效压缩.具体的,所提方案仅仅包含d 随机公开矩阵,这意味着方案的公钥长度仅为(dm2+mn)logq,而在[42]方案中包含2d 个同样大小的矩阵,公钥尺寸达到(2dm2+mn+n)logq.另一方面,消息-密文扩展因子在本节方案中被有效的控制到log q,即在一次加密运算中m2比特的消息仅被加密成m2 log q 比特的密文.与文献[113]和[114]中的方案比较,所提方案也具有空间效率及消息密文扩展因子方面的优势.

设d 为最大分级深度,l′′ 为i层身份的长度,其中1 ≤i ≤d.设安全参数n 在文献[42,113,114]及本文中是相同的.则表6.1给出了空间效率比较的细节.

表6.1　空间效率比较

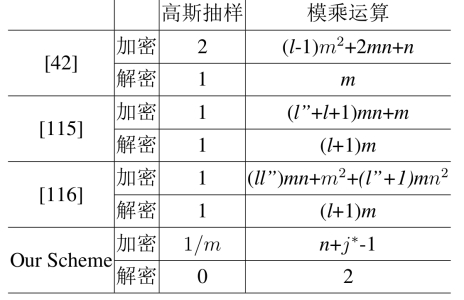
对于格基HIBE而言,主要使用的计算是高斯抽样和模乘运算.对相同长度的消息,我们通过这些主要运算的计算个数比较反感的计算效率.如果仅考虑加密一个比特的消息对应的计算效率,表6.2 给出了计算代价的比较细节.

表6.2　计算效率比较(每比特消息)

注：事实上,可以将本文提出的赋值原则与文献[113,114] 的核心方法结合以设计具有更小参数的HIBE方案.主要思路为我们将身份信息视作(id1,id2,··· ,idl) 其中idi =(idi1,idi2,··· ,idil′′),则我们仅需要l′′ 个矩阵R1,··· ,Rl′′ 即可实现HIBE的设计.不过以上公钥的压缩依然只是常数因子的压缩.因为方案依然需要一组公开矩阵用于格基代理技术的应用.换句话说,只要使用格基代理技术设计IBE,就不得不引入一组公开矩阵,而这必然带来公钥尺寸的增加.因此要实现标准模型下格基IBE方案空间效率的高效实现,应该以规避格基代理的使用作为设计方向.换句话说,寻找在不依赖格“生长”的前提下实现密钥提取，就可以不引入一组公开矩阵而实现公钥尺寸的大幅压缩.

注：上述HIBE仅仅实现选择身份模型下的安全性,如何在适应性选择身份模型下实现格基IBE的安全性,同时保证效率值得深入研究.