因为已知的标准模型下安全的格基HIBE 方案将每一个身份比特赋值为一个随机矩阵,这使得方案的公钥包含至少2d 个随机矩阵.为了缩减格基HIBE的公钥大小,我们提出一个新的公钥赋值原则,利用它可以平均两个身份比特赋值一个随机矩阵.

令R1,··· ,Rd 为d 个按照Dm×m 分布的矩阵.设身份向量为id|d = (id1,··· ,idd),则新型公钥赋值算法如算法1所示.

算法.赋值原则

Initialization: R1,··· ,Rd

Input: id|d =(id1,··· ,idd)

For l=1 to d,do:

输出Ri,其中idi =1,

不输出任何矩阵,当idi =0.(www.daowen.com)

Output: {Ri1,··· ,Rid*}(返回Rij 当idij =1).

因为相应于身份idi1 =···=idid* =1 选定的矩阵{Ri1,··· ,Rid*}在应用于格基代理算法时都将他们的位置因素考虑在内,因此接下来的引理成立.

引理6.1 本节所提的公钥赋值原则是一个身份比特与有序的公钥矩阵集合{Ri|1 ≤i ≤d}间的一一映射.

证明: 只要我们能够证明{Ri|1 ≤i ≤d}的两个不同的有序子集对应两个不同的身份向量,则以上引理自然成立.假设有{Ri|1 ≤i ≤d}的两个不同的子集相应于两个相同长度的身份,则必然存在一个矩阵Rj 属于其中一个子集但是不属于另外一个子集.因此只有一个身份对应满足第j 个分量为1的要求,即idj =1.因此,两个子集相应的身份是不同的.□

假设id|d 是经过随机编码得到的结果,那么id|d 的0-1分布接近平衡.因此,我们的赋值算法平均映射两个身份比特为一个矩阵.从而,本节中仅仅需要d 随机矩阵能够实现标准模型下HIBE的设计.

格基HIBE方案中的密钥提取算法如何使用赋值原则见图6.2所示.

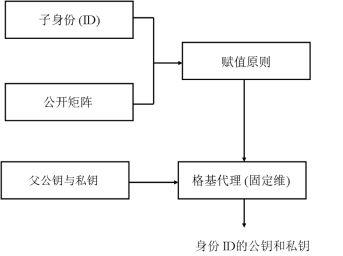
图6.2 提取算法