定理5.2 基于LWE问题的困难性假设,本节的签密tag-KEM是IND-CCA2安全的.

证明: 为了完成定理的证明,我们提供了一系列Game,其中第一个Game是混合签密的IND-CCA2安全Game.而在最后一个Game中任何敌手胜出的优势为零.我们进一步证明任何PPT敌手能够区分这些Game的优势是可忽略的,从而证明我们的方案是IND-CCA2安全的.令Xi 表示在Game i 中b=b′的事件.

Game 0.签密tag-KEM的标准IND-CCA2Game.

Game 1.在Game 1中,如果敌手要求对包含标签τ* 的任意封装进行解封装询问,挑战者总是返回一个错误符号并终止游戏,Game的其他部分与Game 0 一致.

除非τ*被执行解封装询问,否则Game 1和Game 0是一样的,而被询问的概率是1/2l.从而Pr(X0)-Pr(X1)≤1/2l =nelg(n).

Game 2.在该Game中,GenR 算法被按照如下方式修订：

矩阵Biτ*i 是完全随机,而剩余的矩阵Bi(1-τ*i )则是陷门抽样算法的输出.换句话说,挑战者知道陷门基Game 2的剩余部分与Game 1相同.

由于陷门抽样算法输出的矩阵统计接近均匀分布,从而在Game 2中矩阵Bib 均可以被看做是随机的.则Pr(X2)-Pr(X1)=negl(n).即Game 1和Game 2是不可区分的.

Game 3.在Game 3中,挑战者输出挑战封装E =(b,τ*),其中向量b 被选择为Zlmq 中的随机、均匀向量.其他阶段Game 3和Game 2相同.

由LWE问题的困难性Game 2和Game 3是不可区分的.若不然,假如存在一个PPT敌手能以不可忽略的概率区分Game 2和Game 3,则,可以构造一个算法B 能够解决判定型LWE问题.设算法B 收到一个向量b 及相关参数,算法B 要判定b 来自一个均匀分布或是一个LWE问题实现,B执行如下操作:

1.由Genc(1k),GenS 和GenR 算法生成相关的参数以及公钥、私钥对.

2.回答敌手的对称密钥生成预言机、封装预言机以及解封装预言机询问如下:

Sym oracle.选择一个随机向量s,并随机选择一个密钥K ∈{0,1}l.令ω =(skS,pkR),存储(s,ω,K).发送K 给敌手作为对称密钥询问的回复.

Encap oracle.假如τ =τ*,令b,τ*为相应的封装.若不然,利用encap算法计算相应的封装作为答案.

Decap oracle.在解封装询问中,假如τ = τ*,则输出一个错误符号并终止交互.若不然,利用skR 以及pkS 进行解封装运算并将结果发生给敌手作为解封装询问的答案.由于τ 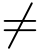τ*,则算法B 总是能够利用私钥完成解封装运算.

3.以后的阶段与Game 2相同,唯一的不同是在挑战阶段将(b,τ*)作为挑战封装.

从而,如果敌手判定是在执行Game 2,则b 是一个LWE问题实例.如果敌手判定在执行Game 3,则b 是一个随机均匀的向量.于是,算法B 以与敌手相同的优势解决了判定型LWE问题.

由于在Game 3中所有PPT敌手的优势是0,从而将4个Game联合起来,我们有|Pr(X0)-1/2|=negl(n).

□

定理5.3 在随机预言机模型下,提出的签密tag-KEM的抗选择消息攻击的强不可伪造性是基于SIS问题的困难假设.

证明: 假如存在敌手A 能够以优势∈攻击方案的sUF-CMA 安全性,在此过程中敌手被运行进行q1 次h1 询问,q2 次对称密钥生成询问,q3 次封装询问.则可以构造一个挑战者C 能够以优势∈求解SIS问题.(www.daowen.com)

假设C 收到一个SIS问题实例(A,2s),其中而s 是一个参数.C 希望能够得到一个小范数的向量e ∈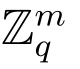满足接下来的性质

首先,C 通过运行Genc 和Genr 来生成全局参数I 和接收者的公钥、私钥

令挑战者的公钥为pkS =A,显然挑战者不知道发送者的私钥.C 发送(pkR,skR,pkS,I)给A 并与A 运行sUF-CMA安全Game.C 维护3个列表Li,i = 1,2,3 用来分别存储对称密钥生成询问、封装询问和h1 预言机的答案.过程如下：

Sym oracle.对一个新鲜的sym询问,C 随机的选择一个向量s 和一个比特串K ∈{0,1}l.令ω =(skS,pkR,s),存储(ω,K)到列表L1.发送K 作为答案.

Encap oracle.对一个非重复的封装询问(ω,τ),C 执行如下操作:

1.检查列表L1 以得到(s,ω,K).（如果列表中未发现相应的记录,则如模拟对称密钥生成阶段所示生成s 和K.同时将(ω,K) 存入L1）

2.选择l 个随机向量ei,满足

3.计算令b=(b1,··· ,bl).

发送(b,τ)作为答案并存储(b,τ,e1)到列表L2.(如果询问是重复的,则为保持一致性返回相同的答案)

敌手可运行Decap算法以验证封装的合法性,此过程中敌手被允许询问h1 预言机.

h1 预言机.对第i 个非重复的询问(s,τ),C 查看列表L2 以得到(b,τ,e1),并计算h1i =Aei(modq).发送h1i 作为答案.最后,C 存储(h1i,s,τ,ei)到列表L3.

当所有的询问完成后,敌手以优势∈生成一个伪造的封装(b*,τ*).

于是,挑战者能够解决SIS问题如下:

首先,C 记b* = (b*1,···),并运行decap算法通过b*1 来得到s* 和e*1,满足Ae*1 =

接下来,查看L2 以得到向量e′1 依然满足

□

所以本章设计的签密tag-KEM是安全的.

由引理5.1,5.2,若将hash函数h2 视作随机预言机,本节设计的混合签密是安全的.