5.2.3.1　签密tag-KEM

Genc.

令n 为方案的安全参数.设q = ploy(n) ≥2,m = (1+δ)n lg q,其中常数δ ＞0.令l = l(n) ≥1 是一个以poly(n) 为限的整数.高斯参数 其中两个抗碰撞的安全hash函数:

GenR.

由陷门抽样算法,接收者生成两个接近均匀分布的矩阵同时输出它们相应的的陷门基 随机的选择2(l -1) 个矩阵其中2 ≤i ≤l,b ∈{0,1}.于是,对i ∈[l]和b ∈{0,1},

GenS.

发送者利用陷门抽样算法生成接近均匀分布的矩阵以及相应的陷门基则pkS =A,skS =T.

Sym.

随机选择向量s ∈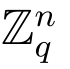并计算K =h2(s).令ω =(s,pkR,skS).

Encap.

1.随机选择τ ∈{0,1}l 并计算h1(s,τ).利用原像抽样函数,发送者计算

2.选择l-1 个随机的差错向量ei 服从分布Φα.对τ =(τ1,τ2,··· ,τl),计算

令b=(b1||··· ,||bl).

则,Encap 算法的输出为(b,τ).(www.daowen.com)

Decap.

接收者执行以下操作完成解封装

1.记b = (b1||b2||,··· ,||bl),其中bi ∈Zmq ,1 ≤i ≤l.假如b 不能记为如上形式,则终止解封装运算.

2.利用τ 的第一个比特确定陷门基T1τ1 并利用该陷门基由b1 计算LWE问题实例对应的向量s 和差错向量e1.

3.计算h1(s,τ),并检查Ae1 =h1(s,τ)和成立.若不然则终止解封装.

4.对每一个i 计算并检查上式得到的向量范数小于等于若不然,则终止解封装运算.

5.计算K =h2(s)作为数据封装机的对称密钥.

5.2.3.2　签密DEM

Enc.

设M ∈{0,1}l 为一个待签密的消息,计算K ⊕M =c(mod2).

Dec.

计算K ⊕c=M(mod2).

将签密tag-KEM和签密DEM结合,可以得到在格上构造带标签的混合签密方案.