5.1.4.1　正确性

设(C,vk,σ)是一个合法密文.因为σ 是Ssign一次签名方案输出的签名,由Ssign方案的正确性,σ 能被Ssign方案的验证算法接受.显然,解密算法能够如加密算法描述的原则固定公开矩阵并得到矩阵.由盆景树算法,解密算法能够抽取一个格的陷门基,从而Step 3成立.

又因为T1 是格的陷门基并且误差矩阵X 是抽取自从而所有T1 and X 的分量都是足够小的.于是E = Tt1C = Tt1(2X+M)(modq)恰恰等于整数环上的Tt1(2X+M)[29].从而,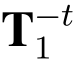E=2X+M.即M=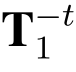E(mod2).

正确性得证.

5.1.4.2　安全性分析

定理5.1 假如LWE问题是困难的,其中误差矩阵是取自分布Φ(l+1)m×(l+1)mα,并且原方案中使用的一次签名方案是强不可伪造的,则本节所构造的PKE方案是IND-CCA2安全的.

证明: 为了证明该定理,我们给出以下4个Game并证明对任意PPT敌手从Game i 到Game i+1 都是不可区分的.

Game 1.Game 1是标准的IND-CCA2安全Game的定义.

Game 2.Game 2同Game 1比较,在解密询问阶段,任何关于(vk*,*,*)的解密询问,总是返回一个错误符号⊥.其他阶段Game 2同Game 1一致.

Game 3.Game 3与Game 2相同,除了在系统建立阶段,如果vk*[ji]=1 则选择一个完全随机的矩阵作为系统的第ji 个公开矩阵.否则vk*[ji] = 0,则公开矩阵被赋值为已知陷门基的矩阵（即陷门抽样算法的输出被定义为公开矩阵）.换句话说,如果vk*[i] = 0,格Λ⊥q(Ai)的陷门基是已知的.

Game 4.在Game 4中,挑战密文(vk*,C*,σ*)中的C* 被完全随机均匀的、并且独立于vk*和σ*的矩阵替代.其他阶段Game 4与Game 3一致.

接下来的4个Claim表明Game 1到Game 4是两两不可区分的.Claim1.假如方案中使用的一次签名方案是强不可伪造的,则Game 1和Game 2对任意PPT敌手是不可区分的.

该结论的证明与文献[98]完全一致,我们省略细节.Claim 2.Game 2和Game 3对任何PPT敌手是统计不可区分的.

证明: 由陷门抽样算法,我们知道陷门抽样算法的输出矩阵所服从的分布式统计接近均匀分布的,从而,如果将某些随机的公开矩阵取代为陷门抽样算法的输出,对任何PPT敌手而言是不可区分的.于是Claim 2成立.□

Claim 3.Game 3和Game 4是计算不可区分的,如果判定型LWE问题是困难的,其中差错分布服从分布.(www.daowen.com)

证明: 假如存在一个PPT敌手A 能够以优势∈区分Game 3和Game 4,则可以构造一个挑战者C 来解决判定型LWE问题.

假设挑战者C 希望区分上的均匀分布和分布{(B,C)|C=BtS+X(modq)},其中与A 交互并模拟或者Game 3或者Game 4如下:

建立阶段.C 生成Ssign方案的签名密钥和验证密钥并分别记为vk*和sk*.令vk[ji*]=1 其中i = 1,2,··· ,l 并且其中i = 1,2,··· ,k-l.运行陷门抽样算法k-l次以输出k - l 个矩阵同时输出格的陷门基.令B = (B0,B2,··· ,Bl) 其中接下来令Aji = Bi 其中i = 1,2,··· ,l 并且其中i = 1,2,··· ,k-l.从而对i=1,2,··· ,k,A=B0 和Ai,是公钥矩阵.

解密预言机.在该阶段敌手可以适应性的询问解密预言机,而挑战者者则应该模拟解密预言机.对任意一个询问密文(vk,C,σ),如果vk =vk*,挑战者输出一个错误符号⊥,若不然,vk 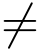vk*,因为vk and vk* 具有相同的汉明重量,于是存在某个位置满足vk[j] = 1并且vk[j*]=0.如建立阶段所示,此时C 知道格Λ⊥q(Aj)的陷门基.从而C 能够运行Bonsai trees算法来生成相应格的陷门基,其中 满足于是挑战者能够利用的陷门基将询问密文解密为消息.

挑战.A 随机的选择两个长度相同的消息Mb,b ∈{0,1},并将它们发送给挑战者C.C 随机的选择一个比特b ∈{0,1},若b = 0 抽取一个服从均匀分布的矩阵C′*（Game 4）,否则，若b = 1 矩阵C′* 是取自LWE实例服从的分布{(B,C)|C = BtS+X(modq)}（Game 3）.接下来,挑战者计算C* = 2C′*+Mb.运行Ssign签名生成C* 在签名密钥sk*下的一次签名σ*.将(σ*,C*,vk*)作为挑战密文发送给敌手.

解密预言机.敌手A 继续询问解密预言机,而挑战者的回复同第一阶段的解密询问一致,所不同的是在本阶段敌手不能够被允许询问任何形如(vk*,*,*)的密文.

显然,如果C′*是一个服从均匀分布的矩阵（或近似服从均匀分布）,2C′*+Mb(modq)依然是均匀的.而如果C′* 是一个LWE问题实例时,2C′*+Mb(modq)所服从的分布与解密算法输出密文服从的分布是一样的.从而,假如敌手能够以优势∈区分自己在与挑战者执行Game 3 或者Game 4,挑战者C 就能以相同的优势区分上的均匀分布和分布

从而解决判定型LWE问题.□

Claim 4.任何敌手在Game 4中胜出的优势为0.

证明: 在Game 4中,因为C* 是完全均匀随机的,从而敌手只能以概率1/2 来猜测比特b,从而Claim 4得证.□

将上述4个Claim联合起来,不难发现任何PPT敌手赢得标准IND-CCA2安全Game的优势是可忽略的.□

5.1.4.3　效率比较

本节所提方案相与文献[27]比较,优势主要体现在其空间效率上.表5.1 给出了两个方案在空间效率上比较的细节,其中vs 表示一次签名和验证密钥的长度之和.

表5.1　效率比较