4.6.4.1　正确性

由上述方案的描述可知,方案所采用的参数能够满足原像抽样函数以及引理2.1的要求,从而盲签名在盲化、去盲过程中的正确性可以很容易的验证.而方案验证签名算法就是GPV的验证算法,从而由GPV签名的正确性可以推得方案的正确性.

4.6.4.2　盲性

定理4.12 本节所述方案满足盲性要求.

证明: 由于签名者收到的盲化消息中的Ac 服从均匀分布,而h 作为一个安全hash函数的输出也近似服从均匀分布,而t 是随机选取的,从而对签名者而言消息μ 服从的分布与均匀分布是不可区分的.设签名者希望通过随机选择Zmq 上的向量和随机选择小于x的自然数来恢复真实消息H.我们证明签名者这样选择所得到的结果分布与均与分布的统计距离为0.

从而盲性成立.□

4.6.4.3　One-more 不可伪造性

文献[38]提出的基于原像抽样函数的GPV签名方案在随机预言机模型下已经证明安全性等价于SIS问题.而我们方案的one-more不可伪造性是基于文献[38]签名方案的存在性不可伪造.假设我们盲签名存在攻击者A能够以不可忽略概率伪造签名,则构造模拟者成功伪造GPV签名,进而解决格上的SIS问题来实现.所以我们的证明中假设模拟者接入一个格上的原像抽样预言机,这一点与文献[97]第一个盲签名证明时接入一个陷门求逆预言机一致.

定理4.13 假设以A,n,m,q,s 为输入的SIS问题是困难的,则我们的盲签名在随机预言机模型下满足one-more不可伪造性.

证明: 假设敌手A 掌握一个概率多项式时间算法φ,以签名人的公钥和相应系统参数以及l个消息与其对应签名为输入,可以以不可忽略的概率∈输出第l+1个消息的伪造签名.则我们可以构造算法S 利用敌手A 以近似概率∈(1-2-ω(log n))来解以A,n,m,q,s 为输入的SIS问题.假设算法S 控制一个Hash随机预言机H,同时接入一个格上的原像预言机[14].同时,算法S 维护两张表L1,L2 分别用来记录hash询问和盲签名询问.(www.daowen.com)

S 发送(A,s,n,m,q)给敌手A,开始游戏.

Hash询问：S 收到敌手发来的第i 个消息Mi 后,S 随机产生向量hi ,满足||hi|| ≤将Ahi 发给敌手,同时在列表L1 中存储Ahi.由引理知,此时Ahi 近似服从均匀分布,因此S 可以完美的模拟hash函数的输出.（若Mi 的消息记录在L1 中,则返回相应记录）.

签名询问：S 收到敌手的第i 个消息μi 的签名询问后,首先在表格L2 中寻找条目(μi,vi),若存在则返回vi 作为签名的应答.否则S把μi 重发给原像抽样预言机,获得消息的盲签名vi,存储(μi,vi)到表格L2,返回vi 作为签名.敌手A 收到签名后可以进行去盲变换得到真实的签名ei.

敌手A 满意后使用概率多项式时间算法φ,以概率∈输出第l+1个消息的伪造签名(Ml+1,el+1).S 从L1 中获得消息Ml+1 的Hash询问记录得到向量hl+1,检查是否有hl+1 el+1 ,若等式成立则S 终止游戏,宣布失败；否则,S 得到两个范数小于的向量,满足Ael+1 =Ahl+1,从而A(el+1-hl+1)=0(modq),且||hl+1-el+1||≤||hl+1||+||el+1||≤从而S 成功的解决了SIS 问题.

以下来分析S 成功的优势,由以上模拟过程可知,S 对hash函数和签名的模拟是完美的,因此,只要hl+1 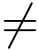el+1 且敌手成功输出伪造则S 总会成功.由引理2.5知hl+1 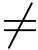el+1的概率大于1-2-ω(log n).从而S 成功的优势大于∈(1-2-ω(log n)).

□

4.6.4.4　效率分析

盲签名方案仅仅利用到了小整数模加、模乘运算和文献[38]的高效抽样方法,所以我们的盲签名实现了较高的计算效率.将我们的方案的效率与[97]中第一个方案进行比较,说明前者在多个指标上有优势.见表4.2.

表4.2说明我们方案在交互的轮数,签名长度上要优于文献[97].此外[97]采用承诺方案来保证签名失败发生时消息对签名者的盲性,而我们的方案可以有效防止签名失败从而允许我们用一个安全的hash函数来代替承诺方案,进一步精简了用户的操作.

表4.3　空间效率比较