分析文献[97]第一方案签名失败的原因（篇幅所限本书略去该方案的描述）,发现[97]中合法签名范数的选择范围较大,同样用户在盲化变换时所选择的向量也有较大的范数,这些直接造成了最后用户去盲后范数可能会溢出,造成签名失败.鉴于以上问题.我们对原像抽样函数的参数进行了调整,要求签名者在一个较小参数下完成抽样,同时要求用户用一个更小范数但是满足引理2.6要求的向量盲化消息,而最后的签名验证则在一个较大的参数s 下进行,采用s 的前提是必须保证此时格上SIS问题的困难性.这样用户在进行去盲变换时,合理增加向量的范数也不会超出验证算法的要求.从而有效地避免了签名失败的发生.同时盲签名的轮数缩小为两轮.

密钥生成

整个方案中n 为安全参数,其他参数都是n 的函数.设签名者利用陷门抽样算法生成一个格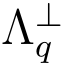(A)及其陷门基B.又设h(·) : {0,1}* →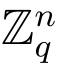是一个安全的防碰撞的hash函数.定义格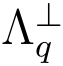(A)上两个离散高斯分布的参数其中 显然两个高斯参数均大于格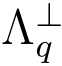(A)的光滑参数,所以以参数s,s′ 进行高斯抽样所抽取的向量e 满足Ae(modq)接近均匀分布.设LM为签名者所签署盲化消息的数据库.综上：公开(A,n,m,q,s,s′,a,x),陷门基B 为签名者的签名密钥.

消息盲化

设原始消息为M,用户计算H =h(M),以零为中心按离散正态分布DZm,aω(log n)随机选择向量c 则

以极大概率成立.若不满足只须重新抽取.由引理2.6 Ac 近似服从均匀分布.任意选择t ∈Z,1 ＜t ＜x,设t-1 为t 在Zq 中的逆元.计算盲化消息：

签名

签名者首先在自己的数据库LM 中寻找μ ,若找到相应记录则终止签名,若μ 不在LM 中,则签名者通过自己掌握的陷门基B 利用原像抽样函数产生盲化消息的签名:(www.daowen.com)

最后,签名者将v 存入列表LM.

去盲

用户得到盲化消息的签名v 后,进行去盲变换：计算e=t(v-c).则向量e 作为签名.

验证

计算H =h(M),验证

否则拒绝签名.