4.5.2.1　完备性

证明: 若ei 是由签名算法直接生成的,则该签名是PSF的一个直接输出.由文献[38]知,Aei =v(mod2q)且 成立.因此ei 能够被Vrf算法接受.

以下证明假如(id,e)是Combine算法的输出,则该签名也能被Vrf算法接受.

简单起见,假定(id,e)是由(id,e1)和(id,e2)组合而成,更一般的情形类似可证.设v1 =(v11,v12,··· ,v1k)和v2 = (v21,v22,··· ,v2k)为对应的消息.则(id,e = e1±e2)是消息v =v1±v2 =(v1,v2,··· ,vk)的签名.事实上,

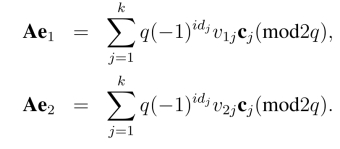
于是

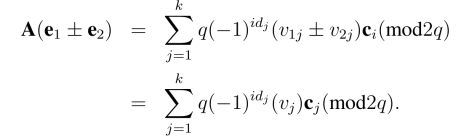
另一方面,成立.

于是(id,e=(e1±e2)mod2q)是消息v=(v1±v2)(mod2)的签名.

□

4.5.2.2　安全性

定理4.10 假如存在一个敌手能够以优势ε赢得LHS方案的不可伪造性游戏,则可以构造一个挑战者能够以2ε/(q-1)的概率解决SIS问题.

证明: 假设存在一个概率多项式时间敌手A,以优势ε 赢得不可伪造游戏,则可以构造一个挑战者C以2ε/(q-1)的概率能够解决SIS问题.

设C 希望解一个SIS问题实例(A0 ∈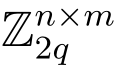,q,n,s,L).C执行如下操作:

(1)令A=qA0(mod2q);

(2)随机选择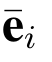使之服从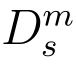，其中i = 1,2,··· ,k,同时确保这些向量线性无关(若不然，重新抽取).

(3)令ci =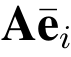(mod2q).

C 发送给A 作为签名者公钥.为了完成以下的模拟,C 维护一个列表用于存储签名预言机的解答.

Sign Query.挑战者需要回答一系列的签名询问前,他首先确保这些询问的新鲜性.如果消息空间Vi 曾经被询问过,则返回相同的答案.对一个新鲜的消息子空间Vi,设该子空间由k 个向量vi ∈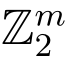表示.C 选择一个标签id(i) ∈{0,1}k,并计算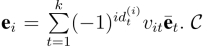存储到L.C 输出

当所有询问结束后,A 以概率ε伪造一个消息v*的签名(e*,id*),(www.daowen.com)

(1)对第一型敌手而言,id*从未被询问过.挑战者计算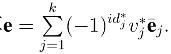

(2)对第二型敌手,id*已经被询问过,不过消息v* Vi.

挑战者从列表中查找则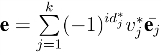是消息v*的另一个签名.

于是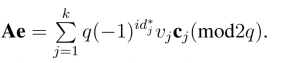

从而A(e*-e)=0(mod2q).

也就是qA0(e*-e)=0(mod2q).

这意味着A0(e*-e)=2kc(mod2q),其中0 ≤k ＜q,c ∈.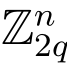

因为A0 均匀随机,而e*,e 是高斯型向量,根据[38]有: A0(e*-e)(mod2q)服从均匀随机分布.从而系数k = 0,1,··· ,(q - 1)/2 是等概率的.另一方面,||e* - e|| ≤而e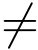* e 以概率1-2-ω(logn)成立.显然,C 在k =0时能够解SIS问题,成功的概率为2ε(1-2-ωlogn)/(q-1).

综上,C 以概率解SIS问题.□

定理4.11 本节提出的LHS方案满足弱数据隐藏性.

证明: 令其中b = 0,1.设j = 1,2,··· ,k,分别是消息向量V0 和V1的签名.因此统计接近高斯分布[38].

设b ∈{0,1}是由挑战者选择的一个比特,e(b) 是由生成的联合签名.

若b=0,e(0)是由e(0)

j 在某线性函数fi,i=1,··· ,s 下提取得到.作为高斯向量的线性组合,e(0)统计接近一个依赖于(Λ,σ,f(V0),f)的高斯分布,其中,f 属于函数集f1,,··· ,fs.

若b = 1,同理可得.又因为,fi(V0) = fi(V1),i = 1,2,··· ,s.因此e(0) 和e(1)所服从的分布统计接近.因此,没有概率多项式时间敌手能够赢得弱数据隐藏游戏.□

表4.2　效率比较

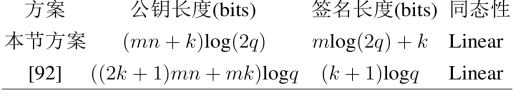
4.5.2.3　效率分析

将我们的方案和一个同样基于格设计的标准模型下安全的线性同态签名方案[92]比较,能够得到如下列表.显然,本节的方案效率上优于同等方案.