4.4.4.1　正确性

证明: 假设hash函数H 是安全的,则给定标签τ,n 个向量α1,α2,··· ,αn 是两两线性无关的.由文献[48]向量hj 可以看做vj 的hash值.又因为ej 是hj 的GPV签名,利用GPV签名的正确性,我们有Aej = hj(modq) 和成立.从而签名算法的输出可以被验证算法接受.

假如一个签名(τ,e) 是联合算法的输出,即以下说明(τ,e) 必然也能被验证算法接受.假设矩阵B 的第i 行恰好是由向量αi = H(τ||i) 的行形式构成.则hj =Bvj(modq)成立.于是,从而,验证算法的条件(a)满足.

另一方面,因为每一个ei 分别是消息vi 的签名,则成立.从而‖e‖ =成立,其中ai ∈{0,1}.即条件(b)满足.

综上,联合算法输出的签名(τ,e)也可以被验证算法接受.

□

4.4.4.2　弱内容隐藏性

为了证明方案满足弱隐藏性,我们需要一个如下的引理[43].

引理4.2 令Λ 是一个格,σ ∈R.对i = 1,2,··· ,k,令ti ∈Zm 并且xi 是依照ti+Λ上的高斯分布（表示为Dti+Λ,σ）抽取的两两独立的随机向量.令c=(c1,··· ,ck)∈Zk 并定义g = gcd(c1,··· ,ck),t = 假设σ ＞‖c‖η∈(Λ) 其中∈是一个任意小的数而η∈(Λ)为格Λ 对应∈的光滑参数.则z=统计接近于Dt+gΛ,‖c‖σ.

该引理说明在离散状态下高斯分布向量的和依然保持高斯分布,而且和分布仅仅依赖于(g,c,t,Λ)而不会依赖于向量xi[43].

定理4.8 本节所提的线性同态签名方案满足弱内容隐藏性.

证明: 显然,高斯参数σ 符合上述引理的条件.在隐藏性所定义的game中,令(V0,V1,f1,··· ,fs)是敌手的输出,其中Vb = span{vb1,··· ,vbk}而b = 0,1.对j = 1,2,··· ,k,令分别为基向量V0 和V1 的签名.由GPV签名知所有这些签名是统计接近高斯分布的.

对一个由挑战者选择的随机比特b ∈{0,1} ,令e(b) 是联合算法联合签名的输出,其中j = 1,2,··· ,k.假设b = 0,e(0) 是在线性函数fi,i = 1,··· ,s 下的一个线性组合.因为e(0)

j 服从的分布统计接近高斯分布DΛ,σ,由上述引理,e(0) 所服从的分布统计接近一个由(Λ,σ,f(V0),f) 决定的高斯分布,其中f 是一个属于函数集合f1,,··· ,fs的线性函数.类似的事实对b = 1 的情况依然成立.进一步的,对i = 1,2,··· ,s,总有fi(V0) = fi(V1)成立.从而e(0) 和e(1) 服从的分布是统计接近的.进而没有任何PPT敌手能够赢得隐私game.□(www.daowen.com)

4.4.4.3　不可伪造性

定理4.9 假如存在一个静态敌手能够在不知道Alice签名私钥的条件下以不可忽略的概率∈赢得线性同态签名不可伪造性的游戏,则存在一个挑战者能够以接近2∈的概率求解SIS问题.

证明: 假设存在一个PPT敌手A 以优势∈赢得不可伪造性Game,其中敌手可以接入随机预言机H q1 次、签名预言机q2 次,则我们可以构造一个挑战者C 来解决SIS问题.

假设挑战者C 收到一个SIS问题实例并希望能够找到一个向量v 满足并且Av = 0(modq).C 发送A 作为线性同态签名的公钥给A.则,A 和C 开始不可伪造性的游戏.为保持一致性,C 维护两个列表Li,i ∈{1,2}用来分别存储随机预言机H 和签名预言机的答案.

Hash询问.当C 收到一个消息子空间的标签τi ,C 首先检查列表L1 以确定是否该询问是新鲜的,若L1 中找到相应的记录,则返回相同的答案α1,··· ,αn 给敌手; 对一个新鲜的询问,挑战者随机的选择服从高斯分布的向量hij 满足其中j = 1,2,··· ,n.接下来挑战者计算Ahij = αj(modq),返回α1,··· ,αn 作为答案.C 将存入列表L1.

签名询问.当挑战者被要求生成子空间Vi 的一个新鲜基向量vij 的线性同态签名时,这里j = 1,2,··· ,k,C 从列表L1 中选择Vi 对应的标签τi .C 同时得到列表L1 中的记录是一个矩阵满足该矩阵的第j 列是向量hij.于是,挑战者计算eij =Hvij(modq).发送(τi,ei1,ei2,··· ,eik)作为线性同态签名.(如果向量vij 之前被询问过,则返回相同的答案)

当所有的询问完成并且敌手感到满意后,敌手A 以概率∈生成消息v*i 的签名(e*i,τ*i).

(1) 假如A 是type 1型敌手,即,标签τ*i 从未被用来执行签名询问,挑战者检查列表L1 发现标签τ*i 及其相应的记录是一个第j 列是向量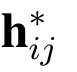构成的矩阵,则H*v*i 依然是消息v*i 的签名.从而,AH*v*i = Ae*i.从而A(e*i -H*v*i) = 0(modq).又因为假如e*i -H*v*i 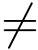0 成立,向量e*i -H*v*i 是一个SIS问题的解.由原像抽样函数e*i -H*v*i 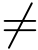0以大于1-2-ω(log n)的概率成立（引理2.5,[38]）.

(2)假如A 是type 2型敌手,也就是标签τ*i 已经被用于签名询问,但是v*i V *i ,挑战者得到列表L1 中该标签对应的记录因为Ae*i =((α*i,v*i),··· ,(α*i,v*i))t =AH*v*i 和v*i /∈V *i 成立,从而A(e*i -H*v*i) = 0(modq) 和e*i -H*v*i 0 成立.于是e*i -H*v*i 是SIS问题的一个解.

接下来我们来分析以上安全规约.在第i 次hash询问中因为向量hij 对任意j =1,2,··· ,n 都是取自高斯参数大于光滑参数的高斯分布,从而Ahij = αj(modq) 统计接近均匀分布[38].于是,挑战者能够以极大概率模拟随机预言机.因为矩阵H 的列向量取自高斯分布,从而eij = Hvij(modq)可以看做高斯向量的线性组合,其中vij ∈Zn2 .由引理4.2,eij 服从的分布是统计接近高斯分布的.从而挑战者能够以极大概率模拟签名预言机.由以上分析,挑战者能够以(1-2-ω(log n))∈+∈≈2∈概率解决SIS 问题.□

4.4.4.4　效率分析

在我们将本节所提方案与文献[43]中的线性同态签名方案进行计算效率比较之前,首先注意以下两个事实：第一是文献[43]中的方案中同时使用了Bonsai tree和PSF两个算法完成对消息的签名,第二个事实是Bonsai tree算法中使用PSF算法作为子算法.与文献[43]比较我们的方案中仅仅使用了PSF算法来完成签名,从而本方案的计算效率小于[43]方案的一半.接下来我们讨论方案的空间效率,表4.1 给出两个方案在公钥长度、签名长度方面的比较细节.不难看出,我们的方案在空间效率上依然高于文献[43]的方案.

表4.1　空间效率比较