令n 为一个素数,参数q ≥βω(log n) 其中β = poly(n).对一个固定的常数c ＞0,参数m ≥cn log q.若参数是一个高斯参数.令L是可以联合的签名的最大个数.抗碰撞的hash函数H 将任意属于(0,1)* 的比特串映射到.在该方案中消息空间为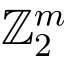.线性函数f 的系数属于{0,1},即,如果f(v1,··· ,vl)=a1v1+,··· ,+alvl 则ai ∈{0,1},i ≤l.设签名者是Alice 而验证者为Bob,本节所设计的格基线性同态签名如下:

密钥生成.Alice运行陷门抽样算法生成一个随机矩阵以及陷门基T ∈分别作为Alice的公开钥和签名密钥.

签名.对一个属于消息空间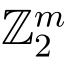 的子空间V,其中v1,··· ,vk 是子空间V 的基向量.τ ∈{0,1}n 是子空间V 的一个标签.Alice按照如下操作签署一个基向量vj ,其中1 ≤j ≤k:

1.计算n 个向量αi：αi =H(τ||i),i ≤n.

2.计算向量的内积hji =〈αi,vj〉(modq),并记hj =(hj1,··· ,hjn)t.

3.利用GPV 签名算法（原像抽样函数）生成向量hj 的一个签名ej .从而,(ej,τ)是一个向量vj 的线性同态签名.

验证.为了验证消息vj 的线性同态签名(ej,τ),Bob如下操作:(www.daowen.com)

1.计算αi =H(τ||i).

2.计算hj =(hj1,··· ,hjn)(modq),其中hji =〈αi,vj〉,i ≤n.

3.接受线性同态签名当且仅当:

(a)Aej =hj(modq);(b)‖ej‖≤

联合.给定公钥A,标签τ 以及数组(ai,ei),其中i = 1,2,··· ,l ,l ≤L,ai ∈{0,1}联合算法输出作为消息的签名.