定义4.6 一个标准的线性同态签名SIGlhs(Kg,Sign,V rf,Combline) 包含如下4个多项式时间算法:

密钥生成（Kg）.该算法输入一个安全参数1n 输出签名者的公钥和私钥(pk;sk).

签名（Sign(M,sk,τ)）.该算法以某个消息集合V 的基向量M ∈V ⊂Fn2,该集合V 的一个标签τ ∈{0,1}*以及sk 作为输入,输出消息M的签名S,表示为S =Sign(M,τ,sk).

验证（Vrf(M,S,τ,pk)）.该判定算法输入向量M,签名S,标签τ 以及公钥pk.假如S 是一个合法签名则算法输出b=1,若不然,输出b=0.

联合（Combline）.令Si 是消息Mi 的签名,参数L 表示可以联合的最大签名个数.输入(pk,τ)和(ai,Si),其中i ≤L,ai ∈{0,1},该算法输出一个消息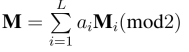的签名S.当前,我们无法实现任意多的签名的联合并依然保证通过验证算法.事实上,我们主要讨论L-limited 线性同态签名方案,在该方案中任意l 个签名能够被联合并保证联合后的签名能够通过验证,其中l ≤L.

一个线性同态签名应该满足如下安全特性.

1.正确性.一个由签名算法正确生成的线性同态签名应该被验证算法所接受.

2.不可伪造性.

定义4.7 称一个线性同态签名在选择消息攻击下是存在性不可伪造的,如果任意多项式时间的敌手赢得以下由挑战者和敌手构成的游戏的优势是可忽略的.

系统建立.挑战者运行Kg算法以生成系统参数和签名者的公私钥对(pk,sk),并将pk发送给敌手.

签名询问.敌手适应性的选择消息空间的一个k 维子空间Vi,设设该子空间的一组基向量为vi1,··· ,vik.对每一个子空间Vi,签名预言机生成一个该集合的标签τi ∈{0,1}n,并计算每一个基向量的签名Sij 给敌手,其中j =1,2,··· ,k.

输出.最后,敌手输出一个τ* ∈{0,1}n,以及一个新消息M*的签名S*.

敌手赢得该游戏,如果输出的签名能够被验证算法接受并且有以下两种情况之一成立：(www.daowen.com)

（1）对所有的i 有τ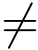* τi 成立(type 1)

（2）若存在某个i 使得τ* =τi 成立,则有M* /∈Vi(type 2).

敌手的优势定义为生成上述伪造签名的概率.

3.隐私性.

线性同态签名的隐私性可分为两个强弱两个概念.本文考虑其中较弱的概念：弱内容隐藏性.

定义4.8 一个线性同态签名方案是弱内容隐藏的,假如任何PPT敌手赢得下述和挑战者进行的游戏的概率是可忽略的:

系统建立.挑战者运行Kg 算法得到(pk,sk)并将他们发送给敌手.

挑战.敌手输出V0,V1,f1,··· ,fs,其中V0 和V1 是消息空间的两个独立的k 维线性子空间用 来描述他们的一组基,其中b = 0,1.函数f1,··· ,fs 对任意i=1,2,··· ,s 满足

为了生成挑战的回应,挑战者生成一个随机比特b ∈{0,1}和一个标签τ ∈{0,1}n.同时利用签名算法生成向量空间Vb 的线性同态签名.签名者利用联合算法生成消息向量的签名σi,并将σi 发送给敌手.

输出.敌手输出一个猜测比特b′,假如b=b′,敌手获胜.

概括的说,所谓弱内容隐藏性指没有任何PPT敌手能够判断是否一个签名是由集合V0 或者V1 的签名联合而来的.