4.3.4.1　正确性

令ω = (y1,y2,π,μ,r,M) 是VES生成算法的一个输出.方案的正确性可以由以下结论推出.

1.因为Alice知道s2,从而Alice完全可以生成一个NIWI证明π,

2.因为Ay1 =A(BTs+e)=Ae=h(M||r)(modq),所以Ae′ =Ay2(modq),

3.又因为c=(y1+y2-Bμ)=(e+e′)(modq),从而Ac=(h(M||r)+Ay2)(modq),

4.而 成立,所以

即,一个合法的VES可以通过验证,正确性得证.

4.3.4.2　存在性不可伪造性

定理4.6 对任何以不可忽略的优势∈攻击方案的存在性不可伪造性的敌手A,随机预言机模型下总可以构造一个挑战者C 可以以接近∈的概率求解SIS问题.

证明: 假设一个PPT的敌手A 可以以概率∈伪造一个VES,敌手被允许进行q1 次随机预言机询问,q2 次VES询问和q3 次判决询问,我们来构造一个有效的挑战者C 可以求解一个SIS问题实例.

假设C 收到一个SIS问题实例(A,n,m,q,s).C 希望得到一个向量e,满足：

C 计算B 满足ABt =0(modq).C 发送(A,B,n,m,q,s)给A,其中A 是签名者的公钥而B是判决者的公钥.C 维护两个列表L1,L2 以分别存储随机预言机询问和VES询问的应答.

Hash询问.收到一个消息Mi,C 在列表L1 中查找消息Mi,假如这样的条目存在于列表则返回相同的应答.若不然,消息是新鲜的,C 随机选择一个比特串r ∈{0,1}k 以及向量ei ～DZm,s,0.C 计算hi = Aei(modq).(ei,ri)作为该询问的应答.C 将(ei,ri,mi,hi)存入列表L1.

VES生成询问与签名询问.不失一般性,假设A 在执行VES签名询问前已经执行过随机预言机询问.为了回答一个针对hash值hi 的VES询问,C 首先确保hi 从未被询问过,假如hi 是新鲜的,C 选择向量s1i,s2i ∈Znq 以及一个小向量 C 在列表L1 中找到与hi 对应的记录(ei,ri)（该记录既是普通签名询问阶段的答案）.为了生成消息的一个VES,如VES签名生成算法所示,计算y1i,y2i,μi.C 最后构造一个NIWI证明πi.发送ωi =(y1i,y2i,πi,μi,ri,Mi)作为VES.最后,C 存储(ωi,s1i,s2i,e′i,ei,hi)到L2.

判决询问.显然C 可以利用L2 的记录打开一个VES以完成判决询问.

当所有询问完成后,A 以概率ε 输出一个伪造的可以由L1 得到ej,并通过敌手A 抽取一个向量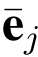,满足

假如ej 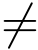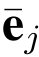,C 立即得到一个SIS问题的解.由文献[38],ej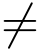 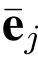的概率至少是1-2-ω(log n).从而C 得到一个SIS问题的解的概率为(1-2-ω(log n))∈.□(www.daowen.com)

4.3.4.3　不透明性

定理4.7 假如存在A 以概率∈,并接入随机预言机q1 次,进行VES询问q2 次以及判决询问q3 次,来攻击方案的不透明性,我们可以构造一个挑战者C 以概率 来解决 问题.

C 将(B,n,m,q,s)输入引理4.1的算法[28],其中设输出为

于是A 作为签名者的公钥,B 作为判决者的公钥.在开始游戏之前C 首先猜测一个描述i*.C 维护L1 和L2 来存储随机预言机询问和VES询问的答案.

Hash询问.设询问消息为Mi,首先在L1 中查找Mi 以确保消息新鲜.对一个新鲜的消息询问,C 执行以下操作:

1.若i=i*,令hi* =Ay(modq).选择一个ri* ∈{0,1}k 并发送(hi*,ri*)作为应答.

2.若i 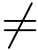i*,随机选择ei 和ri ∈{0,1}k 满足 计算hi = Aei(modq).(hi,ri)作为本次询问的应答.将(hi,ri,hi,mi)存入L1.

签名询问.由于C 掌握格Λ⊥q(A) 的陷门基,从而他总可以生成一个小向量e 满足Ae=hi(modq)作为消息的签名.

VES生成询问.对消息Mi,C 确保Mi 是新鲜的（通过L2 的记录）.假设Mi 新鲜,C首先在列表L1 中获得消息Mi 对应的hi.此后,挑战者执行以下操作：

1.若i=i*,随机选择μi* ∈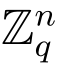和一个小向量e′i*,计算y2i* =BTμi* -y+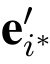(modq).C 生成一个NIWI证明πi*.令(y,y2i*,μi*,ri*,πi*)作为VES询问的应答并将其存入L1.

2.假如i 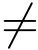i*.C 可以直接利用VES生成算法算法生成对应的VES作为回复,并将VES存入列表L2.

判决询问.假如i = i*,C 终止并宣布失败.若i 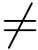i*,C 可以利用两个列表的记录来打开VES获得对应的普通签名.

最后,敌手以概率∈输出一个普通签名(Mj,ej,rj),该消息从未执行过签名询问和判决询问.假如j =i*（发生的概率为1/(q2-q3)）,C 可以解决上述LWE问题.具体的,因为(ej,rj)是一个普通签名并且j =i*,于是y=Btsj+ej(modq)和成立.从而C 得到向量s 满足y=Btsj +ej(modq).假如j 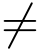i*,C 终止游戏并宣布失败.

C 可以完美的模拟以上询问过程除非消息Mi* 被执行判决询问,而此事件发生的概率为q3/q1.综合以上分析,C 求解LWE问题的概率为 .□