4.2.6.1　匿名性

定理4.4 本节提出的强指定验证者环签名满足无条件匿名性.

证明: 注意到r′和t 是LWE问题实例,由LWE问题的困难性,向量r′和t 近似可以看作随机向量,从而不会泄露任何签名人的信息.而向量e = (e1||e2||··· ,||el||eb) ∈Z(l+1)mq统计接近离散高斯分布,从而e 也不会泄露签名人的身份.□

4.2.6.2　不可传递性

由签名副本的生成算法知,由指定验证者生成的签名副本和真实签名者生成的签名满足不可区分性,从而,指定验证者无法使任何人相信该签名是由Alice签署的,从而满足不可传递性.

4.2.6.3　不可伪造性

定理4.5 假如存在一个攻击者能够以概率∈生成伪造的强指定验证者环签名,则可以构造一个挑战者以接近∈的概率解决SIS问题.

证明: 假设存在一个PPT敌手A 以概率∈伪造一个强指定验证者环签名,其中敌手可以进行q1 次h1 预言机询问、q2 次h2 预言机询问、q3 次签名询问和q4 次指定验证者的验证询问.我们可以构造一个挑战者C 来求解SIS问题.

假设挑战者C 收到一个SIS问题实例 C希望得到一个向量v满足和Av = 0(modq).令A = (A1||A2||···||Al||Al+1),Ai ∈发送Ai,i ≤l 作为环成员的公钥,Al+1 作为指定验证者的公钥给敌手A.挑战者维护3个列表Li,i=(1,2,3)分别用来存储随机预言机h1,h2 和签名询问的答案.

h1询问.收到消息Mi,i ≤q1 后,挑战者首先检查列表L1,如果该消息存在于列表L1,则返回相同的答案h1i 给A.若不然,对一个新鲜的消息,挑战者随机选择向量vi 满足以及一个随机向量t′i ∈Znq,并计算Avi =h1i(modq),返回h1i 作为该询问的应答.挑战者将(Mi,vi,h1i,t′i)存入列表L1.

h2询问.当收到消息Mi 要求执行h2 询问时,挑战者依然首先查看列表L2,假如该消息存在于列表中,则返回相同的应答否则,挑战者选择两个随机向量和ri,将h2i 作为应答并将(Mi,ri,h2i)存入列表L2.(www.daowen.com)

签名询问.当挑战者被要求生成消息Mi 的签名时,挑战者由列表L1 查找到对应的向量(vi,h1i,t′i),并由列表L2 得到ri,h2i.接下来,挑战者计算σi =(vi+h2i)(modq).挑战者继续计算：

其中差错向量xi1,xi2 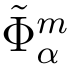～.挑战者在L3 中存储Mi,σi,r′i,ti.于是挑战者将(σi,r′i,ti)发送给敌手作为应答.

指定验证者验证询问为了验证签名(Mi,σi,r′i,ti),挑战者由列表L1,L2 查找相应的h1i,t′i 和h2i.于是σi+h2i = vi(modq)成立.接下来,挑战者可以如验证算法所述验证该签名成立.

执行完所有的询问后敌手以概率∈生成一个消息的伪造签名(Mi*,σi*,r′i*,ti*).于是挑战者可以借助(Mi*,σi*,r′i*,ti*)以及3个列表的记录来求解SIS问题实例的解.

首先,由列表L1,L2 获得h1i* 和h2i*.于是,挑战者可以得到一个向量ei*,有||ei*||≤和Avi* =h1i* 成立;

接下来,由L1 得到vi*.则Avi* =h1i*(modq);

最后,若ei* vi*,则Avi* =Aei*(modq),即A(vi* -ei*)=0(modq).又因为

于是

即挑战者得到了一个SIS问题实例的解.假如ei* =vi*,则挑战者终止游戏并宣布失败.

接下来分析挑战者成功的优势.在敌手能够成功的给出伪造签名的前提下,挑战者能够解SIS问题实例的条件是ei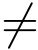* vi*.注意到e*i 和v*i 都是向量h1i* 在陷门单向函数fA(x)=Ax(modq)下的原像.由文献[38],h1i*的原像的数目至少是2ω(log n),从而,ei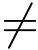* vi*的概率至少是1-2-ω(log n).于是挑战者的优势至少是(1-2-ω(log n))∈.□