4.2.4.1　正确性

显然,利用格的陷门基可以得到一个陷门单向函数fA(s) = (Ats+x)(modq)的唯一原像s.因此,在一个合法的SDVS签名(σ,r′,t)中,Bob可以由r′ 和t 中计算得到r和t′,从而可以计算h1(M,t′)和h2(M,r).于是Bob可以通过计算σ+h2(M,r)=e(modq)获得真实的签名向量.显然该签名满足和(A,B)e = h1(M,t′).从而一个合法签名能够被验证算法接受,正确性得证.

4.2.4.2　不可传递性

由方案的模拟算法知,签名的副本与真实的签名是统计不可区分的,从而验证者Bob无法向第三方出示该签名并使对方相信该签名来自Alice.

4.2.4.3　强性

由签名的构成可知,Alice对消息的签名是以Bob的公钥“加密”的密文出现的,从而签名与随机比特串不可区分，只有利用对应的密钥“解密”获得真正的密文才可能验证签名的正确性.方案满足强性.

4.2.4.4　不可伪造性

定理4.3 假如SIS问题是困难的,在随机预言机模型下本节所提方案满足存在性不可伪造性.

证明: 为了推出矛盾,我们假设存在一个PPT敌手A 能够以不可忽略的优势∈,伪造一个Alice是签名者、Bob是指定验证者的SDVS签名,其中,敌手可以进行q1 次h1 预言机询问,q2次h2预言机询问,q3 次签名询问已经q4 次指定验证者验证询问.则我们来构造一个挑战者C 以优势(1-2-ω(log n))∈来求解SIS问题.

设挑战者C 收到一个SIS问题的实例并希望能够得到一个向量v,满足：

令

发送A1 作为Alice的公钥,A2 作为Bob的公钥给敌手.为了维持一致性,挑战者维护3个列表Li,i=(1,2,3)用来分别存储h1,h2 随机预言机询问和签名询问的答案.(www.daowen.com)

h1询问.对任意消息Mi 的h1 询问,其中i ≤q1,挑战者首先查看列表L1,若相应的消息存在于列表L1 则返回列表中的h1i 给敌手;若不然,消息是新鲜的,挑战者随机的选择一个向量vi 满足||vi||≤并计算Avi =h1i(modq),再选择一个随机向量返回h1i 作为该次询问的应答.挑战者将(Mi,vi,h1i,t′i)存入列表L1.

h2询问.当消息Mi 执行h2 询问时,其中i ≤q2,挑战者查看列表L2 以确定该询问是新鲜的,如不然则返回同样的答案.对一个新鲜的h2 询问,挑战者选择随机向量和r ∈Znq,返回h2i 作为询问的答案并将(Mi,r,h2i)存入列表L2.

签名询问.对任意消息Mi,其中i ≤q3,不妨设消息是新鲜的,挑战者由列表L1得到(vi,h1i,t′i),并由列表L2 得到r,h2i.接下来,挑战者计算σi = (vi + h2i)(modq),r′ =(At2r+x1i)(modq)及ti =(At2t′+x2i)(modq),其中误差向量x1i,x2i 服从分布Φmα .则(σi,r′i,ti)作为该消息的SDVS发送给敌手.挑战者将(Mi,σi,r′i,ti)存入L3.

验证询问挑战者通过列表L1,L2 的记录可以打开任何一个由挑战者生成的指定验证签名,并向敌手证明该签名是正确的.

在所有询问结束后,敌手A 以概率∈给出一个伪造的SDVS签名(Mi*,σi*,ri*,ti*).挑战者以敌手的输出以及自己存储与三个列表的记录来解决SIS问题如下：

首先,挑战者分别从列表L1,L2 中获得h1i* 和h2i*.从而挑战者得到向量ei*,满足

接下来,由列表L1 得到vi*,并有Avi* =h1i*(modq)成立;

最后,查看是否有ei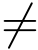* vi* 成立.若ei* =vi*,挑战者终止游戏并宣布失败.若成立则有

由

可知成立.从而挑战者得到一个SIS问题的解.

以下分析挑战者成功的优势.挑战者能够成功的条件是ei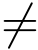* vi* 成立.由于向量ei*和vi*都是hash值h1i*在陷门单向函数fA(x)=Ax(modq)下的原像,由文献[38],h1i*在该陷门单向函数下的原像个数至少为2ω(log n),从而ei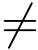* vi* 成立的概率至少为1-2-ω(log n).所以挑战者能够解决SIS问题的概率至少为(1-2-ω(log n))∈.□