设n为安全参数,

定义两个安全的、抗碰撞的hash函数

设签名者为Alice,指定验证者为Bob,则提出的格基SDVS方案如下所述:

密钥生成.Alice和Bob分别利用陷门抽样算法,分别生成自己的公钥矩阵和以及他们的私钥

签名.设消息M ∈(0,1)*,Alice 生成该消息的SDVS如下:

1.随机选择向量t′ ∈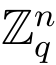 并计算h1(M,t′).依照分布DZm,s 选择一个随机的小向量;

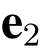2.计算向量e1：

于是Ae1 =h1(M,t′)-Be2 和则(A,B)e=h1(M,t′)并且

3.随机选择一个新的向量r ∈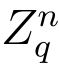,计算(www.daowen.com)

4.选择两个误差向量x1,x2 服从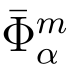 分布.计算:

将(σ,r′,t)作为消息的签名.

验证.Bob收到消息M 的SDVS签名(σ,r′,t)后验证如下:

1.利用自己的私钥TB 由LWE实例r′,t 中求解r,t′,进而计算两个hash值h1(M,t′),h2(M,r).

2.计算σ+h2(M,r)=e(modq).

3.验证

上式成立则输出“1”,否则,输出“0”.

副本模拟.Bob可以利用自己的密钥TB 计算向量e,满足(A,B)e = h1(M,t′),其中t′ 为一个随机向量.接下来,Bob可以通过签名算法生成两个向量r′ = Btr+x1(modq)和t=Btt′+x2(modq).由于e 和r′所服从的分布统计接近均匀分布.从而Bob可以生成一个与真实签名不可区分的模拟签名.