4.1.4.1　匿名性

定理4.1 本节方案实现了环签名者身份的完全匿名性.

证明: 环签名是大维数格上的一个范数较小的向量,而矩阵A 包含所有环成员的公钥信息.注意到这些公钥的位置是完全平等的,因此从任何一个成员的公钥出发都可能得到该消息的签名v,即每一个成员都可能生成此签名,因此验证者不能从v 中分解出签名者公钥的任何信息,他只能以1/l 的概率推测签名人的身份,l 是成员的个数；而要通过大维数格上的一个小向量得到小维数格上的一组小基（签名密钥）来对应签名人的身份更是不可行的.进一步地,消息的环签名v 作为SampleD 算法的输出近似服从格上的正态分布[38],因此任意两个环成员的签名或者一个环成员对两个消息的签名服从的概率分布对验证者而言是不可区分的.所以环签名实现了无条件匿名性.□

4.1.4.2　存在性不可伪造性

定理4.2 假设存在不是任何环成员的概率多项式时间敌手A 能够至多通过Q 次环签名询问以不可忽略的概率∈伪造新的消息μ（假设μ 是一个hash值）的合法环签名,其中消息μ 从未在签名询问中被询问过.则可以构造算法B 以近似∈/kQ1 的概率来解大维数格上的SIS问题.

证明: 设算法B 得到一个格上的SIS问题实例(A,q,m′,s),其中：

m′ =lm1+2km2,l,k 为正整数,b 取0或1.算法B 希望得到一个范数小于等于的向量v,有Av=0(modq)成立.

为此算法B 充当挑战者与敌手A 进行以下询问应答的游戏,鼓励敌手攻击环签名方案.首先算法B 维护一张列表L 以保持询问回应的一致性.L 用于跟踪敌手A 的环签名询问.不失一般性,假设敌手A 在签名询问前已经经过了Q 次正确的hash询问并得到了消息的正确hash函数值.设待签名的消息为μ(1),μ(2),··· ,μ(Q).B 计算比特串p 的集合T,p 取不是任何μ(1),μ(2),··· ,μ(Q)前缀的最小的比特串,于是|p|＜k（注：由文献[45]集合T 可以在多项式时间内计算得到）.算法B 在集合T 中任意取一个p = (p[1],··· ,p[t]),其中t=|p|,算法B 生成环签名的公钥如下：(www.daowen.com)

1.若

2.运行随机格抽样算法生成2t 个随机矩阵及其对应格的陷门基Ti.

将矩阵A0 作为环签名方案中环成员公钥级联得到矩阵,矩阵 对应一个环签名方案中的环公开参数矩阵.以(A0,Abi)来初始化敌手A,让敌手A 来攻击以上环签名.

签名询问：算法B 为消息μ(j)生成环签名的过程如下：首先在列表L 中寻找此消息的签名记录vj,若找到此消息则返回列表中相应的vj 作为签名.若消息不在L中,设i 为第一个满足μ(j)[i]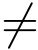p[i]的位置,B 掌握格的陷门基,则

其中,将vj 作为消息的签名发送给敌手,同时将此消息签名对存入列表L.

在敌手A 对所有签名询问满意后,敌手A 以概率∈生成第Q+1 个消息μ(Q+1) 的伪造签名vQ+1 .算法B 检查p 是否是消息μ(Q+1) 的前缀,如果不是μ(Q+1) 的前缀,算法B 终止游戏,宣布失败.否则p 是μ(Q+1)的前缀,则矩阵是由矩阵A0 和k 个U(b)i 级联得到.所以算法B 可以通过添加必要的子阵并调整子阵的顺序将矩阵Aμj 变为A ,同时在vQ+1 上添加0向量并按照相同的顺序调整矩阵分量的位置,由vQ+1 得到向量v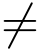0,满足: Av=0(modq),由模拟过程知从而算法B 成功得到SIS问题的一个小整数解.

分析算法B 成功的优势：算法B 成功的关键是随机选取的集合P 中的比特串p 应该是第Q+1 个消息的前缀,此概率接近1/kQ,从而算法B 成功的概率近似为∈/kQ.□