3.4.2.1　正确性

证明: 由签名算法知,向量vj0 是PSF的输出近似服从高斯分布且

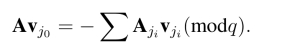
即Aμv = 0.另一方面vj0 是PSF的输出, 以至少1-2-n的概率成立.又因为对任意i = 1,2,··· ,k* 成立,从而||v|| ≤ 因此一个合法签名以极大概率能够被验证算法接受.□

3.4.2.2　存在性不可伪造性

定理3.2 假设存在概率多项式时间的静态选择消息攻击者（敌手）A 经过Q 次签名询问后能够以不可忽略的概率∈伪造一个“合法”签名,则我们可以构造一个算法B 以近似概率∈/kQ 解决SIS问题,其中k 为hash函数的输出长度.

证明: 假设算法B 得到一个SIS问题的实例其中

B 希望得到一个范数小于等于的向量v 满足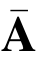v=0(modq).为此,算法B充当模拟者以A 为子程序求解SIS问题.

假设A 已经获得了Q个真实的hash值μ1,μ2,··· ,μQ .B 计算比特串p 的集合P ,p取不是任何μ1,μ2,··· ,μQ 前缀的最小的比特串.则|p|≤k(由[45],这样的集合可以在多项式时间内计算得到,且集合P 中至多有kQ 个元素).算法B 在集合P 中任意取一个p,设p 中一共有t 个位置为1.分别用t1,··· ,tt 表示为1的位置.则算法B 进行如下操作生成公钥:

1.随机抽取|p|-t 个陷门格Λ⊥q(Bj) 及其陷门基Tj ∈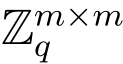,其中Bj ∈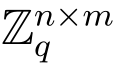,j ＜|p|且j 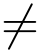ti,i=1,2,··· ,t.并令A= 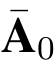.(www.daowen.com)

2.当i ＜|p|时,令Ati = 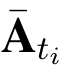,其中0 ＜t1,t2,··· ,tt ＜|p|且pti = 1.其他位置按照下标的顺序依次定义Aj =Bj .

当i ＞|p|时,依次令Ai =.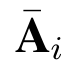

从而公钥为A,A1,··· ,Ak.B 将公钥连同公开参数n,m,q,s,k 一起发送给敌手并开始询问应答游戏.为保持一致性,算法B 维护列表L,用于记录签名询问的答复.

签名询问hash值为μi 的消息Mi 在进行签名询问时,算法B 首先检查列表L,如果在列表中找到μi,则返回相应的记录vi.否则,算法B 可以生成的签名.

由于p 不是μi 的前缀,而μi 作为hash函数的输出满足伪随机性,从而在的前|p|个位置中除去t1,t2,··· ,tt 这些位置,还存在为1的位置（概率为设该位置为t′,则该位置对应的公钥矩阵At′ = Bt′ ,从而算法B 掌握了格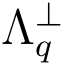(Bt′) 的陷门基.于是算法B 可以借助格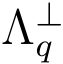(Bt′)的陷门基利用签名算法生成消息μi 的签名vi .B 发送vi 给敌手A 并将(vi,μi)存入列表L.

在敌手A 完成Q 次签名询问并感到满意后,A 以概率∈输出一个新消息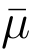 的伪造签名v* ,满足 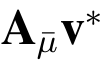= 0(modq)和其中j* 是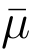 的汉明重量,而矩阵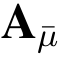的含义同上述签名算法.算法B 检查p 是否是 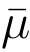的前缀,如果不是,则B 终止并宣布失败.若不然,p 是 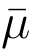的前缀,则矩阵A 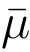是由这些矩阵中的部分矩阵级联而成的.根据矩阵 之间的关系,B 可以在相应位置级联矩阵将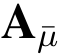 变为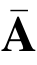 .同时在向量v* 相应的位置上级联0 向量得到 .从而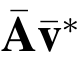 = 0(modq) 且 从而B 得到SIS实例的一个合法解.

分析: B 伪造的所有的公钥矩阵都近似服从均匀分布,而对A 的每个签名询问,算法B 均可以给出近乎完美模拟,即给出的签名统计接近高斯分布.从而算法B 是否伪造成功仅仅取决于比特串p 是否是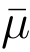 的前缀.由于比特串p 是在P 中随机选择的,而 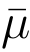是一个伪造的消息,从而比特串p 是 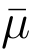的前缀的概率接近于是算法B成功的概率接近为□

3.4.2.3　效率分析

首先假设hash函数的输出总是0,1均衡的.在基本参数(n,m,q)相同的前提下,将本文方案与著名的Bonsai trees签名进行效率比较,结果表明:相比盆景树签名,新方案的公钥长度和签名长度都有了较大程度的缩减.详细信息如表3.1所示.

表3.1　效率比较