密钥生成

设n 为方案的安全参数,c 为大于1的常数,

设h(·) : {0,1}* →{0,1}k 为安全的hash函数.由[39],签名者得到矩阵及格上的陷门基T.随机、独立的生成k 个矩阵A1,A2,··· ,Ak .则签名公钥为(A,Ai),i=1,2,··· ,k,T 为签名密钥.(n,m,q,s,k)为系统参数.

注: 作为一个要在标准模型下实现安全性的方案,本节使用hash函数的目的只是为了实现消息到{0,1}k的变换.本节为便于讨论,假定hash函数的输出是0-1均衡的.事实上我们方案的安全性完全不依赖hash函数的随机性.因此,本节方案虽然使用了hash函数,但方案却是在标准模型下证明安全的.

签名

设消息为M ∈{0,1}*,签名者执行以下操作:

1.计算μ=(μ[1],μ[2]··· ,μ[k])=h(M),其中μ[i]为第i 个分量.(www.daowen.com)

2.签名者首先利用μ[i]的值（0或1）决定是否选择矩阵Ai:若μ[i]=1 则选择矩阵Ai,否则μ[i]=0 则放弃矩阵Ai.设利用以上原则一共选定了k*个矩阵: Aj1,Aj2,··· ,Ajk*(注:由于hash函数的输出是均衡的因此通常k* =k/2).

将这k*个矩阵与A 依次级联得到一个新的矩阵

3.按高斯分布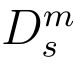 随机选择k* 个整数向量vj1,vj2,··· ,vjk* .则i=1,2,··· ,k*.计算∑Ajivji(modq).

4.计算vj0 ←SamplePre(T,s,-∑Ajivji(modq)),记v=(vj0||vj1||··· ,||vjk*).则消息的签名为v.

验证

验证者计算μ = (μ[1],μ[2],··· ,μ[k]) = h(M) ,并利用μ[i] = 1 或μ[i] = 0 选择矩阵Ai（见签名过程第二步）.将选定的矩阵与矩阵A 依次级联得到一个新的矩阵Aμ =A||Aj1||···||Ajk* ,其中k*为μ 的汉明重量.验证Aμv=0(modq),通过以上验证则接受签名,否则拒绝该签名.