盆景树算法（Bonsai trees）在提供强大设计能力的同时,其自身的弊端也显而易见.为了实现格的“生长”一组庞大的矩阵必须实现级联.这导致公钥、签名的空间效率低下.为了改进格基代理算法的效率,后续的,密码学家分别提出了实现较少格维数增加的、具有“左右抽样”功能的格基代理技术[41]和不需要增加格的维数,即在固定维数上实现格的“生长”的格基代理技术[42].这些格基代理技术为格密码效率的提升提供了工具支持.例如我们介绍固定维数的格基代理算法如下: 首先介绍一类小范数的矩阵R.

若R(modq) ∈是可逆,则R 称作在Zm×m上是Zq可逆的.设σ 为的高斯参数,若一个矩阵是Zq可逆的,且服从分布,则我们称该矩阵服从Dm×m 分布.从而对适合的参数,矩阵服从分布Dm×m时将以极大概率具有较小范数.

引理2.10 令m ＞2n log q,q ＞2.除至多q-n 部分外,对几乎所有的n维矩阵A ∈存在一个PPT 算法输出一个矩阵R ∈Zm×m 统计接近分布Dm×m.进一步的,给定格Λ⊥q(A)的一个陷门基T 以及一个矩阵R,存在一个PPT 算法,BasisDel(A,R,T,σ),输出Λ⊥q(AR-1)的一个陷门基TB,以极大概率满足:

证明: 该引理的证明细节见文献.本书仅仅不加说明的给出引理中定义的两个ppt算法.

令格Λ⊥q(A)的陷门基为T,σR 为高斯参数.

算法.小矩阵生成

输入: Λ⊥q(A),T,σR.

1.对i=1 到m,执行:

ri ←PreSample(Z,T,σR,0).

2.输出R=(r1,r2,··· ,rm),若该向量在Zm×m上可逆,否则,重复步骤1.(www.daowen.com)

输出:R ∈Zm×m

算法.陷门基生成

输入: (A,T,R,σ).

1.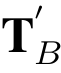 =RT,

2.变型上的基.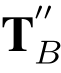

3.利用RandBasis算法将 变为TB.

输出:TB.

□