闵可夫斯基定理给出了格上最小范数向量的范数下界.这两个定理的证明都相对复杂,因此,本书忽略了其证明过程.不过,有一点是肯定的,闵可夫斯基定理的证明不是构造性的,也就是说该定理并没有给出一个能够找到范数满足的向量的方法.事实上,对一个一般的格而言,无论是计算第一逐次最小λ1 或是寻找其最小向量都是困难的.最短向量问题(Shortest Vector Problem,SVP)和最近向量问题(Closest Vector Problem,CVP)是格上定义的两个最典型和最基本的困难问题.其中SVP在随机规约下被证明是NP-hard问题[24],而CVP问题则在确定性规约下证明是NP-C问题[25].

定义2.7 (SVP)设B是格Λ 的一组基,d ∈R,SVP问题就是在格上寻找一个非零向量u 满足: 对任意格上的向量v ∈Λ,有||v|| ≥||u||成立.而Gap-SVP问题就是要判断λ1 是否小于实数d.若λ1 ≤d,则输出YES,否则,输出NO.

定义2.8 (CVP)给定B 是格Λ 的一组基,t 为目标向量.CVP问题就是在格上寻找一个非零向量u 满足: 对任意格上的向量v ∈Λ,有||v-t||≥||u-t||成立.记dist(Λ,t)=||u

-t||为目标向量到格的距离.

（Gap-CVP问题）给定格Λ 的一组基和目标向量t,已知有理数γ ＞1 及有理数r,Gap-CVP问题要求判断dist(Λ,t)属于YES实例或NO实例.其中YES实例中dist(Λ,t)＜r,NO实例中dist(Λ,t)＞γr.

事实上,对格SVP和CVP问题而言,其近似问题(Approximate)依然是困难的.也就是说,在格上,对恰当的参数γ(n),即使确定一个格向量使其范数小于γ(n)λ1,依然是困难的.

定义2.9 SIVP问题（Shortest Independent Vector Problem）.给定一个n 维格Λ 及其一组基B,有理数r,SIVP问题要求输出n 个线性无关的格向量S,使得||S||≤rλn.

Regev提出一个带差错的学习问题（Learning with Errors,LWE）.LWE问题包含查找（Search）型和判定（Decision）型两种.

定义2.10 (LWE问题)给定参数(n,m,q),令s ∈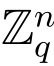,χ是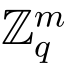上的一个差错分布.令As,χ 为通过计算{A,Ats+x(modq)}得到的概率分布,其中A ∈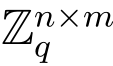是一个选择均匀随机的矩阵而差错向量x 是选自分布χ.Search型LWE问题定义为:通过给定分布As,χ 的多项式个抽样,以不可忽略的概率求解出向量s.Decision 型LWE问题是要求区分As,χ 分布和上的均匀分布.

Regrev证明LWE问题的困难性等价于利用量子算法求解最坏状态下的SIVP问题和Gap-SVP问题的困难性[26].后来,Peikert通过适当放大参数q 给出了LWE问题到标准格问题的经典规约[27].

标准LWE问题中差错分布χ 是一个离散高斯分布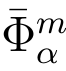,其中高斯偏差为

设R 上的连续高斯分布为Dα,其中α 为标准方差,则 可以按照如下操作实现:

1.按照高斯分布Dα 抽取m 个数η1,η2,···ηm ∈R.

2.计算ei =qηi(modq),其中符号·表示近取整运算.

3.记e=(e1,··· ,em)为LWE问题的差错向量.

如文献[28]所述,在LWE问题中即使差错向量取自较之“标准”差错高斯分布的形状更宽的分布D(Zm,α),困难性依然满足.令LWE(m,q,α)为差错高斯参数为α 的标准LWE问题的缩写,上述事实可以由以下引理表述.

引理2.1 LWE(m,q,α)问题的困难性可以推出LWE(m,q,D(Zm,α))问题依然是困难的.

引理的详细证明由文献[28]给出.

基于LWE问题容易构造一个陷门单项函数,其陷门为格上的一组陷门基（范数较小的基,下同.设格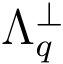(A)的一组陷门基T,则由LWE问题定义的陷门单项函数{A,y = Ats+x(modq)}可以如下求解.首先计算Ty=Tx(modq).由于陷门基T 和差错向量x 都具有较小的范数,因此对于足够大的参数q 我们以极大概率有Tx(modq)=Tx（整数）成立[29].接下来计算差错向量x = T-1Tx(modq).从而利用A,e,y 通过解线性方程组可以求出向量s.

特别指出,文献[30]指出LWE问题具有良好的鲁棒性,这可能为基于LWE问题设计抗泄露密码提供了先天的优势[31].

定义2.11 小整数解问题(Short Integer Solution Problem,SIS):给定一个均匀随机的矩阵和参数n,m,q,β .SIS问题的目标是找到一个非零的整数向量v ∈Zmq ,满足‖v‖≤β 和Av=0(modq).

SIS问题可以看作格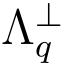(A) 上的近似SVP问题.文献[32]证明了平均状态下的SIS问题和最差状态下的SIVP问题等价.

小结: 与基于数论假设的困难问题比较,格上困难问题具有一些新颖的特点,这些特点能够为基于其设计的密码方案提供崭新的特点和功能.例如:(www.daowen.com)

1.量子安全性: 格上困难问题在量子攻击下依然保持困难性,截至目前,没有发现量子算法在求解格上困难问题时拥有比标准算法明显的优势.研究者普遍相信格问题能够保持量子环境下的安全性.这也使得格密码成为当前最典型的后量子密码之一.

2.平均状态下的困难性与最坏状态下困难性实现等价.Ajtai证明了格问题在平均状态和最坏状态下是等价的[11].这使得格密码的安全性可以基于格上最坏问题的困难性假设.这一特点相对其他困难问题而言也是巨大的优势.

事实上,格的这一特点,使得在随机均匀产生的格上搭建格密码系统就能确保攻破该密码系统的难度与解决最坏状态下格问题一样.既便于格密码的设计,又能实现高的安全性.显然很多基于其他困难问题设计的密码系统不具备该特点,例如,基于大整数的素分解问题设计的格密码.我们究竟如何选择一个N能够确保分解N是困难的? 首先,我们不能寄希望于第三方帮助我们生成这样的N,显然那样将导致第三方可能攻破我们的方案.因此,别无选择N只能由自己产生.不过如何产生N呢?如格密码一样随机生成一个N显然是不可取的.因为至少一半可能是偶数很容易实现分解(即使是奇数也可能容易分解).或许,如读者想到的那样,可以先选两个素数,让它们相乘得到N.不过,我们依然需要小心的是对某些选择的素数可能导致由它相乘得到的N可能容易在特殊分解算法下实现分解.总而言之,虽然我们相信大整数素分解问题在最坏状态下是困难的,但如何确保N分解的难度是在最坏状态下没有明确的结论.

3.格上涉及的计算都是相对简单的模乘运算,其计算效率较高.

4.LWE和SIS问题都保持着线性的结构,这一特点也为格上设计保持同态性的全同态密码提供了便利.截止目前,全同态加密算法及F2 上的同态签名方案都是基于格设计实现的[33,34],[35–37].

2.1.3.1　陷门格与陷门基

对偶格:给定一个格Λ(B),定义Λ 的对偶格Λ* 为以B 为基向量的线性空间中所有与Λ 中向量内积为整数的向量的全体.即:

利用对称性,我们有(Λ*)* =Λ 成立.利用对偶格的定义可得如下结论,若B 是格Λ 的基,则B* =(B-1)t 是对偶格Λ*的基.

利用Gram-Schmidt正交化过程,可以将格的一组基B 进行正交化,得到该基的Gram-Schmidt正交型并记为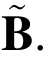 需要强调的是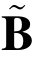中向量除第一个向量外其他向量均不再是格中向量.接下来的引理给出了格的Gram-Schmidt正交基与其对偶格的Gram-Schmidt正交基之间的联系.

引理2.2 [38]设{b1,··· ,bn}是按照范数大小排列的一组基,{d1,··· ,dn}是其对偶基并且是按照范数大小的反序排列的.则对所有i ∈[n] 成立.进一步的

在格密码中一般使用两类特殊的、定义在Zq 上的满秩、整数格.这两类格可以如编码理论中的线性码一样用矩阵给出方便、具体而形象的描述.设和向量y ∈Znq,其中n,m,q 为相关参数,定义

即所有与矩阵A 的行向量模q 正交的向量构成格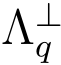(A).而格(A)则由向量y 所在的格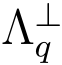(A)的陪集中向量构成.

Ajtai 给出了一个能够生成Λ⊥q(A)与格上一组小范数基（陷门基）的概率多项式时间算法.这使得基于格(A) 设计密码方案成为可能,该算法成为格公钥设计过程中的基本工具,大大推动了格公钥密码的发展[11].不过,Ajtai给出的陷门基生成的效果并不理想,其输出向量的范数达到O(n2 log n).因此在实际该算法时,为了确保格上陷门基不被敌手计算得到,必然要增大系统的参数,这显然增加了系统的开销,限制了系统效率的提升.后续的,Alwen和Peikert提出了一个更高效的生成格及其陷门基的算法[39],使得陷门基的输出范数缩小到这为缩小格密码系统的安全参数、提升其实现效率提供了理论保证.后来,2012年,Micciancio和Peikert又提出一种范数更小、更利于生成的高效新型陷门生成算法,并实现了与陷门基使用场景的衔接.本文依然从陷门基应用的角度开展格密码的介绍.本节通称Ajtai及Alwen的算法称之为陷门抽样算法,并以引理的形式给出算法的描述.

引理2.3 (陷门抽样算法)[39]给定参数q =poly(n)和m ＞5n log q,存在一个概率多项式时间（PPT）算法以1n 为输入,输出一个矩阵和一个满秩集合S ⊂Λ⊥(A),其中矩阵A 的分布是统计接近均匀分布的,并且‖S‖≤O(n log q).进一步的,集合S可以被有效的变型为格Λ⊥q(A)的陷门基T.

算法.陷门抽样算法

输入: A1 ∈

(1)生成其中,U为非奇异矩阵,GP+C ⊂Λ⊥(A1).

(2)计算A2 =-A1(R+G)∈

(3)计算

输出:A=(A1,A2)和S.

注: 陷门抽样算法的关键是的计算.读者可以参考[39]得到各矩阵的具体计算和产生方式.篇幅所限,本节不再详细展开.