由格的定义知,任意格的两组等价基之间相差一个单位模矩阵.显然,单位模矩阵有无穷多个,因此,格的基是不唯一的,有无穷多个.一个很自然的问题是: “对于给定的一个格,有哪些固定的标签可以因为格的固定而固定下来?”或者说,“对一个格而言在基变化的外表下有哪些本质的、不变的因素存在?”

2.1.2.1　行列式

定义2.6 格的行列式定义为:detΛ(B)=

由于格的不同基向量间相差一个单位模矩阵,有以上定义不难发现,通过不同的格基计算得到格的行列式是相同的.即:

格的行列式从几何上看等于其每组格基所对应的基本平行多面体的体积.以下介绍一个计算格的行列式的方法.

设b1,b2,··· ,bn 是一组线性无关向量,令b*1,b*2,··· ,b*n 分别为其Gram-Schmidt正交化向量.因此由Gram-Schmidt正交化过程可知:

则可以利用格的基向量的Gram-Schmidt正交化向量范数之积来计算格的行列式.

定理2.4 设B={b1,b2,··· ,bn}是格Λ(B)的一组基,则det(Λ(B))=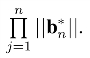

证明: 设B* =(b*1,b*2,··· ,b*n),则由Gram-Schmidt正交化过程可知,B* =BU,其中矩阵U为对角线元素全部为1的上三角矩阵.

所以:

两边计算行列式得:

□(www.daowen.com)

2.1.2.2　逐次最小

因为格是向量的集合,是离散的,所以在格中必然存在非零向量,使得其欧几里得范数最小.设在格上第一最小的范数为λ1.若以原点为“球心”做一个半径为λ1 的开球,则该球内仅仅包含一个非零的格向量,事实上是格的最小向量.

一般的,令B(0,r)={x ∈Rm|||x||＜r},一个给定格Λ的第i个逐次最小λi定义为:

即第i个逐次最小λi被定义为以原点为中心,包含i个线性无关的格向量的最小球体的半径.

不同的范数都可以定义相应的逐次最小的概念,不过每个逐次最小的值以及哪个向量实现相应的逐次最小却可能因为范数的不同而不同.例如:

是格Λ = {v ∈Z2|v1 +v2 = 0(mod2)}的一组基.显然如果考虑l1-范数,λ1 = 2,则向量b1 = (2,0)T是第一逐次最小向量.不过当考虑欧几里德范数时,向量b1 =(2,0)T 不是第一逐次最小对应的向量.

逐次最小的概念与格上向量存在必然的联系,使得逐次最小在格理论的研究中起到举足轻重的作用.首先我们有如下结论成立.

定理2.5 设一个n维格Λ,及其n个逐次最小值λ1,λ2,··· ,λn,则存在线性无关的n个格向量v1,v2,··· ,vn ∈Λ,使得||vi||=λi,其中i=1,2,··· ,n.进一步的,利用逐次最小作为工具可以给出格上最小向量满足的上下界.

定理2.6 设b1,b2,··· ,bn 是n维格Λ的一组基,令b*1,b*2,··· ,b*n 分别为其Gram-Schmidt正交化向量.则

定理2.7 (闵可夫斯基第一定理)设格Λ是一个n维满秩格,则

定理2.8 (闵可夫斯基第二定理)设格Λ是一个n维满秩格,则