1.IGBT的开通机理数学描述

不同于常规的IGBT模型，该IGBT模型重点考虑了IGBT的极间寄生电容对其开关过程影响。在实际分析中，寄生电容影响下IGBT的开通过程可分为如图8-1所示的4个阶段。图中，R_gint为栅极内电阻，C_gc、C_ge为极间寄生电容。其开通的具体过程如下：

阶段1：在栅极驱动电源U_g的作用下，栅-射极电压U_ge上升至开启电压U_ge（th）。IGBT仍处于关断状态，端电压电流均不变化。

阶段2：栅极被继续充电，集电极电流I_c随着U_ge按一定规律增加，集-射极电压U_ce因负载效应迅速减小，直至接近U_ge。

阶段3：U_ce继续下降至接近通态压降；由于密勒效应，等效输入电容C_in非常大，引起栅极电压平台的出现，栅极电流几乎全部注入C_gc。

阶段4：U_ce下降到通态压降并基本不变，密勒效应消失，IGBT处于导通状态；驱动电源U_g继续对栅极充电。

若以栅极电压U_ge为分析对象，则图8-1的4个阶段均可等效为驱动电压U_g经栅极回路电阻R_g和栅极回路电感L_g对该阶段等效输入电容C_in充电，即U_ge满足：

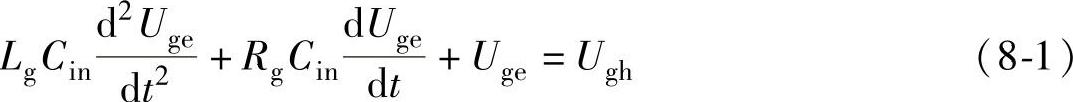
式中 U_gh——U_g高电平；

R_g——栅极回路电阻，R_g=R_gon+R_gint，R_gint为栅极内电阻，R_gon为栅极充电外接电阻；

L_g——栅极回路电感。

等效输入电容C_in为

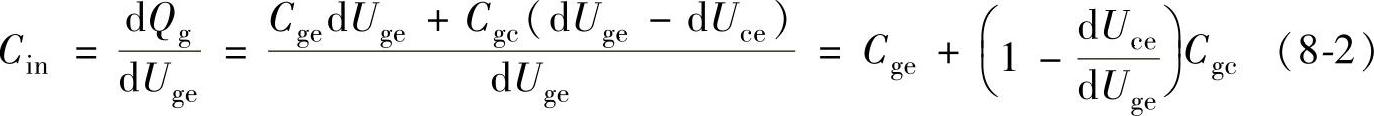
在开通过程中，各极间寄生电容会有较大的变化，由此会带来C_in的较大变化。但分别对于图8-1的每个阶段来说，C_in的变化范围不大，计算中可以对其分段线性化处理。

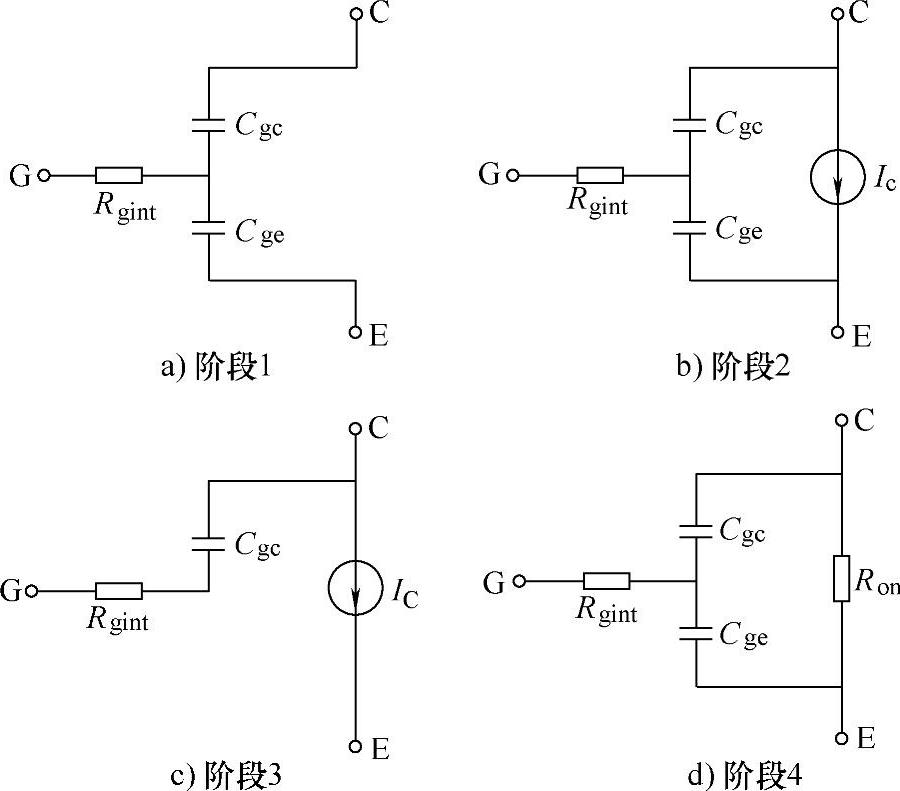
图8-1 IGBT的开通过程电路模型

由上面的二阶微分方程可得到各阶段栅-射极电压U_ge的变化规律。

1）若R²_gC_in>4L_g，则

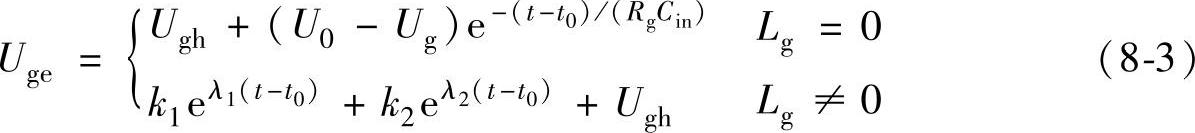
式中 U₀——该阶段的栅极初始电压；

t₀——该阶段初始时间。

且

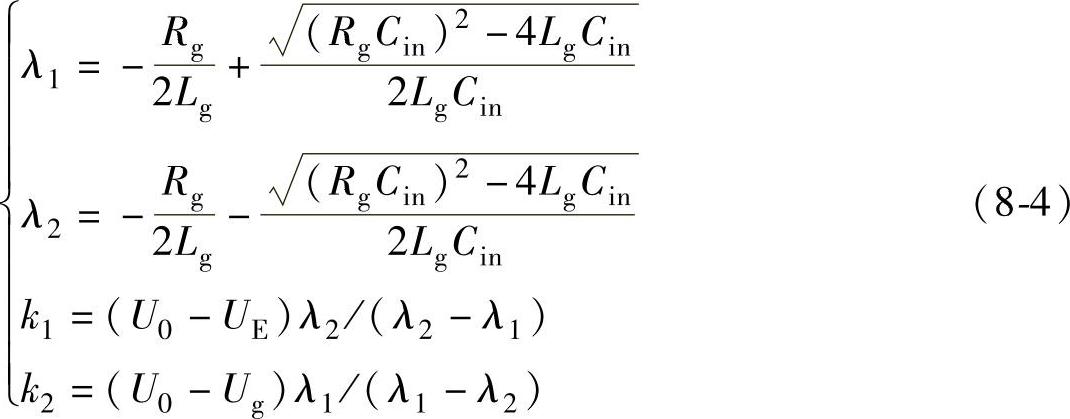
2）若R²_gC_in=4L_g，则

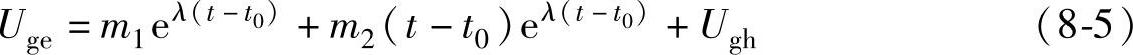
式中

3）若R²_gC_in<4L_g，则(www.daowen.com)

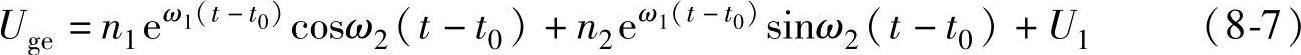
式中

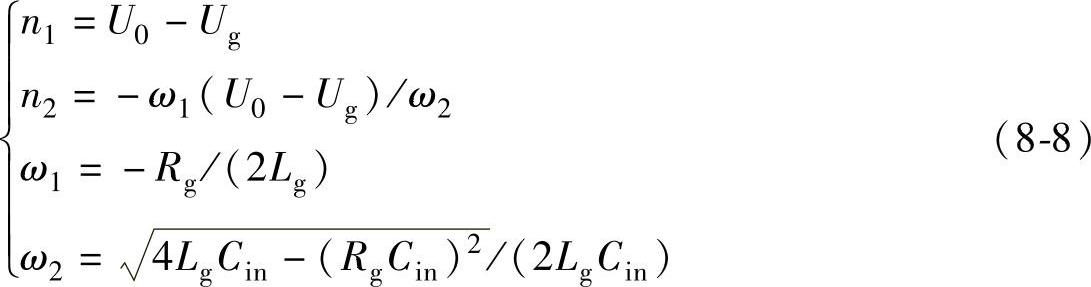
从上面的分析中可以看出，当栅极充电电阻R_g选得太小（R²_gC_in<4L_g）时，可能会引起栅极回路震荡，不利于器件的安全稳定运行。为了器件的安全运行，R_g应选得合适。

在开通过程（阶段2、3）中，集电极电流I_c与U_ge的关系满足器件的转移特性。该特性可以通过器件数据手册或实验获得，并用二次函数来近似，即满足

I_c=a（U_ge^-Uge（th））2+b（U_ge^-Uge（th）） （8-9）式中 a、b——相应的系数，可由最小二乘拟合得到。

2.IGBT的关断机理数学描述

IGBT的关断过程与开通过程相反，也分为4个阶段，具体过程如图8-1所示。与开通过程的分析类似，此时各阶段的栅极电压U_ge满足：

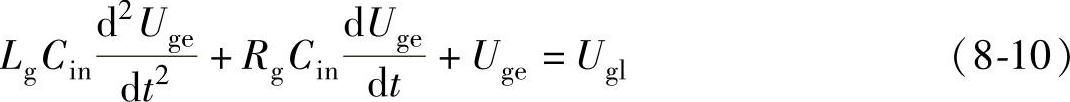
式中 U_gl——驱动电压低电平。该方程的解答与开通过程类似。

与开通过程不同的是，关断过程的第4阶段（对应于图8-1的阶段1），当U_ge降到开启电压U_ge（th）以下时，IGBT阳极电流I_c不会立即消失，而是会以拖尾电流的形式逐渐变为0。拖尾电流是由IGBT的制造工艺和运行条件决定的，在计算中，可以用指数函数进行模拟。

式中 α——IGBT中PNP晶体管的电流放大系数；

I_c（on）——IGBT的通态电流；

t₀——拖尾电流初始时间；

τ——拖尾时间常数。

3.IGBT的稳态特性数学描述

在该模型中，当IGBT达到开通稳态后，其电阻随栅极电压、通态电流而变化，并不简单地采用图8-1中的通态电阻R_on来表示。模型采用压控电流源来模拟IGBT通态电流I_c（on），电压控制量为端电压U_ce，二者满足器件的输出特性，该特性可通过器件数据手册或实验获得。典型的输出I-U曲线如图8-2所示。在每个固定的栅极驱动电压U_g下，可拟合为

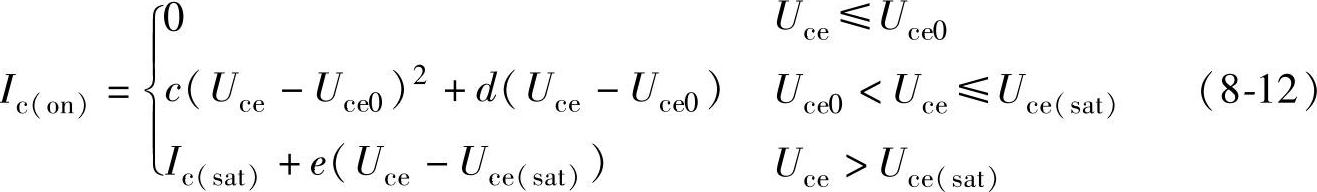
式中，U_ce0——IGBT的初始导通电压；

I_c（sat）——^该Ug下的饱和电流；

U_ce（sat）——^Ic^达到Ic（sat）时的压降（如图8-2所示）；

c、d、e——相应的拟合系数。

在实际使用过程中，驱动电压U_g通常比较固定，可以对可能使用到的U_g分别求出拟合系数c、d、e。

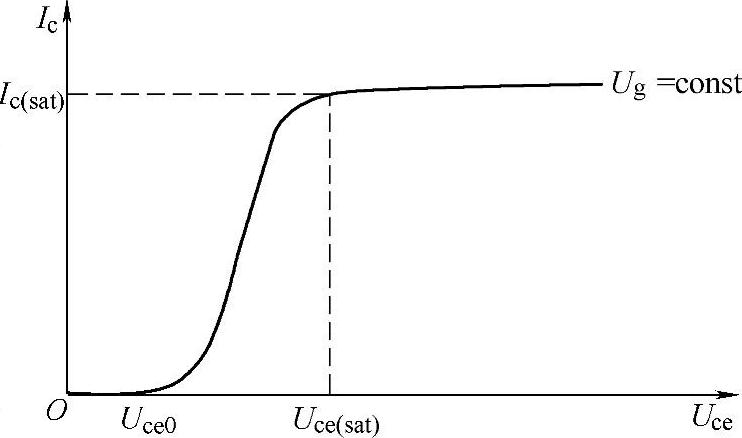
图8-2 IGBT的典型输出特性