平衡状态下的PN对于电力电子变换器来说没有任何用处，PN结的主要特征是具有单向导电性，这一特征在平衡状态时表现不出来，只有在偏置条件下才显示出来。在PN结上外加电压称为对PN结的偏置，PN结的偏置分两种，即正偏与反偏，P区加正，N区加负叫正偏置，反之P区加负，N区加正叫反偏置。在讨论PN偏置时，为分析的方便，作两点假设如下：

1）空间电荷区的自由载流子完全耗尽，忽略在空间电荷区的载流子的电离和复合。偏置的PN结会有电流流过，忽略空间电荷区以外的欧姆压降，即可以认为外加的电压全部加在空间电荷区。

2）假设注入的少数载流子浓度远小于半导体内多数载流子的浓度，此时载流子浓度不均而产生的扩散区域内对应的漂移电场可以忽略。

可以简单地分析此假设的合理性，尽管在有电流通过PN结时也会有电压降落在中性区上，但是对大多数PN结器件来说，中性区的长度与面积之比甚小，且载流子的密度比较高，因而电阻很小，而空间电荷区则因载流子耗尽而具有很高的电阻。因此，外加电压在中性区的降落与在空间电荷区上的降落相比可忽略。

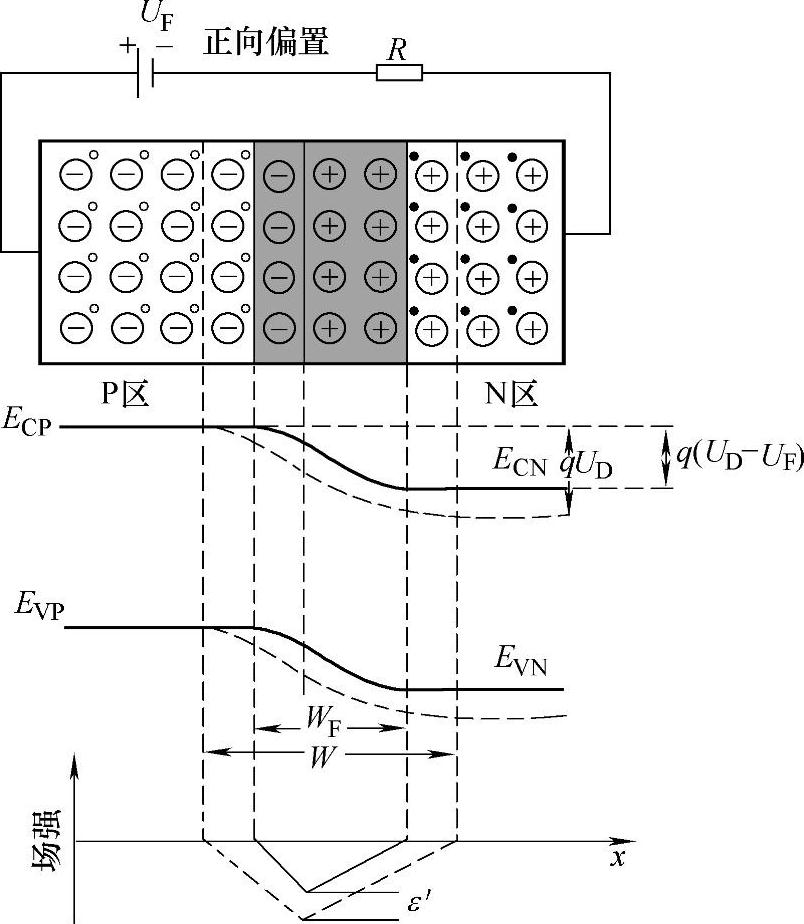
图3-8 正向偏置PN的电场和能带分布

当PN结正偏置时，设外加正向电压U_F，U_F的正端接P区，负端接N区。由前面的假设，U_F全部加在势垒区上，在势垒区内产生一个外加电场ε′，其方向与原来的自建电场方向相反，从而削弱了势垒区电场的强度。由于势垒区中电场被削弱，势垒区中的空间电荷数量将减少，势垒区宽度由W变窄为W_F。同时，势垒区两边之间的电势差降低，由原来的U_D降至U_D-U_F，势垒高度也就由原来的qU_D降至q（U_D-U_F）。与平衡PN结相比，正偏置的PN结的能带图发生了变化，P区和N区的费米能级也不相等，两者的差变为qU_F，正偏置的PN的示意图如图3-8所示。此时势垒的宽度为

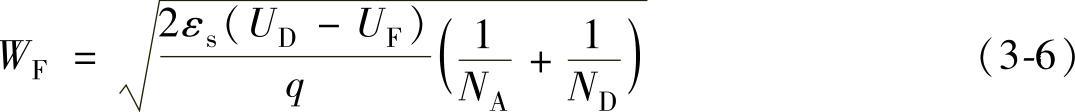
当PN结处于正偏置时，在外加电场作用下，空间电荷区的电场被削弱。因此，载流子的扩散运动大于漂移运动，电子从N区扩散到P区，空穴从P区扩散到N区，形成扩散电流，即N区和P区的多子扩散到对方，使对方的少子增加，这种现象称为PN结的正向注入效应，或者“少子注入”效应。

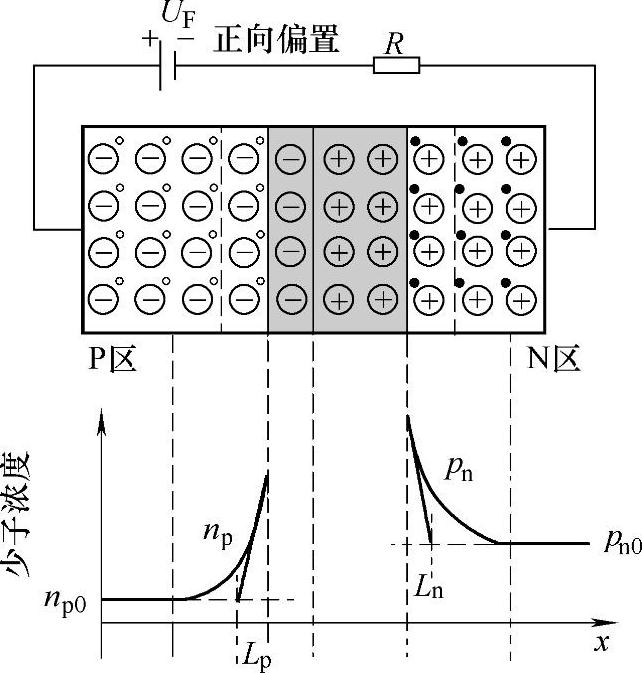
图3-9 PN结正向偏置时的少子注入

不论是N区注入到P区的电子，还是自P区注入到N区的空穴，在注入之后都成了所在区域的非平衡少子。它们主要以扩散方式运动，即在边界附近积累形成浓度梯度，并向体内扩散，同时与所在区域的多子进行复合，浓度逐渐降低，最终形成一个稳态分布。图3-9给出了P区和N区中这种注入少子浓度分布的示意图。

图3-9中，L_n为空穴扩散长度，L_p为电子扩散长度。一般的，P区和N区宽度远大于少子扩散长度，所以在远离PN结的区域，非平衡少子因全部复合而浓度趋于零，即远离PN结的区域内，少子的浓度趋于该区域内的平衡值p_n0或者n_p0。角标0表示平衡状态，p_n0表示在N区内，空穴在平衡状态下的浓度。

额外载流子的注入，即少子的增加，提高了P区和N区的载流子密度，改善了PN结的导电性。由于额外载流子的注入量与正偏压的大小有关，因而导电性的改善程度依赖于电压的大小。这就是电导调制效应，是PN结的基本效应之一，也是双极型器件的主要特征之一。如果从PN结的外特性来看，只考虑PN中流经的电流和其等效电阻，表现为电流增大，电阻减小，这正是双极型器件通流能力强的根本原因。

可以综合来看PN结中的电流的形成过程。首先，正偏压将使多数载流子在中性区漂移，其方向与注入的少数载流子的扩散方向相反。这样，N区中有电子向PN结方向漂移，在漂移过程中不断地与从P区注入的扩散空穴相复合，未被复合的电子则被注入P区，作为P区的少数载流子继续向纵深扩散，在扩散过程中与P区中向PN结方向漂移的多数载流子-空穴相复合。随着扩散电子在P区的深入，电子扩散电流逐渐转化为空穴漂移电流，到注入电子被全部复合时，扩散电流即全部转化为漂移电流。类似的过程也会在N区发生。如果电子和空穴的复合只发生在两侧的中性区而不发生在空间电荷区，那么，正偏置电路中总的正向电流就是流过PN结的电子扩散电流和空穴扩散电流之和。图3-10中给出了正偏置下PN结中电流的分布，尽管在中性区的每一个与结平面平行的截面上通过的扩散流与漂移流的比例不同，但总电流密度对任何平行截面必须是相等的，这才能够保持电流的连续性。如果改变正偏压的大小，例如令其增大，使空间电荷区的电场进一步减弱，阻挡少数载流子注入的势垒进一步降低，则中性区的额外载流子密度将随之上升，因而正向电流相应增大。

如上面的分析所示，正向偏置电路中总的正向电流就是流过PN结的电子扩散电流和空穴扩散电流之和。经过相关公式推导，可以得出正向偏置PN结中总的电流密度为

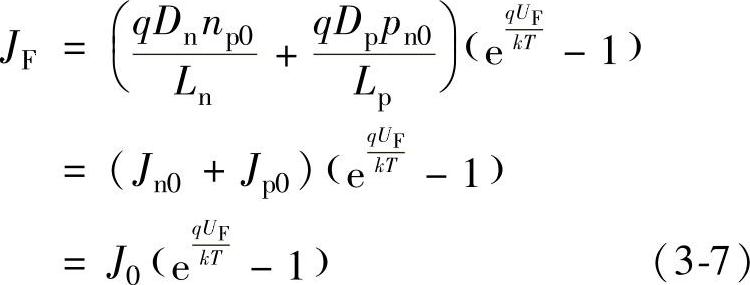
式中 D_n——电子扩散系数；

L_n——电子扩散长度；

D_p——空穴扩散系数；

L_p——空穴扩散长度；

J₀——饱和电流；

J_n0——饱和电流中电子电流；

J_p0——饱和电流中的空穴电流。

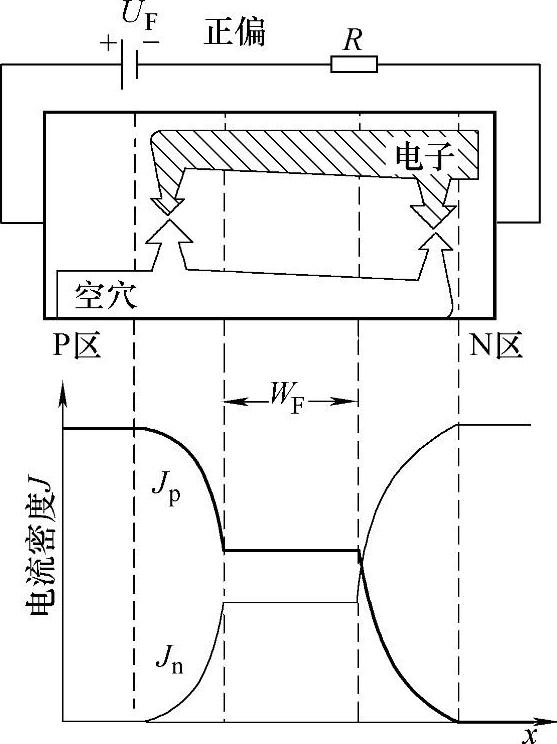
图3-10 正向偏置下 PN结中电流的分布

该式也从数学角度准确地表达了PN的电导调制效应。

从图3-10中可以看出，在正偏置PN结流过势垒的电流中（图中间平直的一段），空穴和电子的作用一般并不相同。图中，P区的掺杂浓度大于N区的掺杂浓度，则流过势垒电流中空穴电流比例更大。当PN结两侧的掺杂浓度差别较大时，流过势垒的电流几乎全是由一种载流子产生。P⁺N结的电流几乎全是空穴电流，PN⁺结中的电流几乎全是电子电流。使用注入效率γ来表征PN结中空穴和电子电流之间的关系。

对于空穴电流更大的PN结，注入效率为(www.daowen.com)

对于电子电流更大的PN结，注入效率为

对于本节所讨论的PN结有

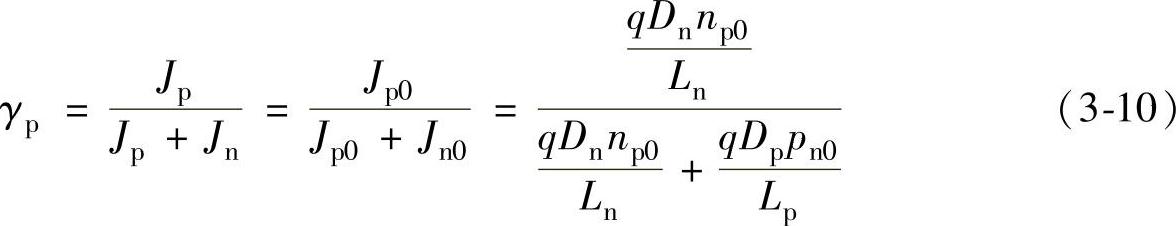
注入效率也是PN结的特征参数之一，在后面的多PN结器件分析中有重要作用。

当PN结反偏置时，设外加正向电压U_R，U_R的正端接N区，负端接P区，U_R全部加在势垒区上，在势垒区内产生一个外加电场ε′，其方向与原来的自建电场方向相同，从而增强了势垒区电场的强度。由于势垒区中电场被增强，势垒区中的空间电荷数量将增加，势垒区宽度由W变宽为W_R。同时，势垒区两边之间的电势差增加，由原来的U_D增至U_D+U_R，势垒高度也就由原来的qU_D增至q（U_D+U_R）。与平衡PN结相比，反偏置的PN结P区和N区费米能级的差变为qU_R，反偏置的PN的示意图如图3-11所示。此时势垒的宽度为

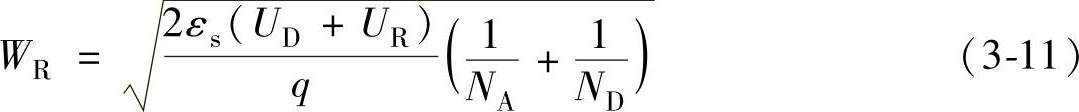
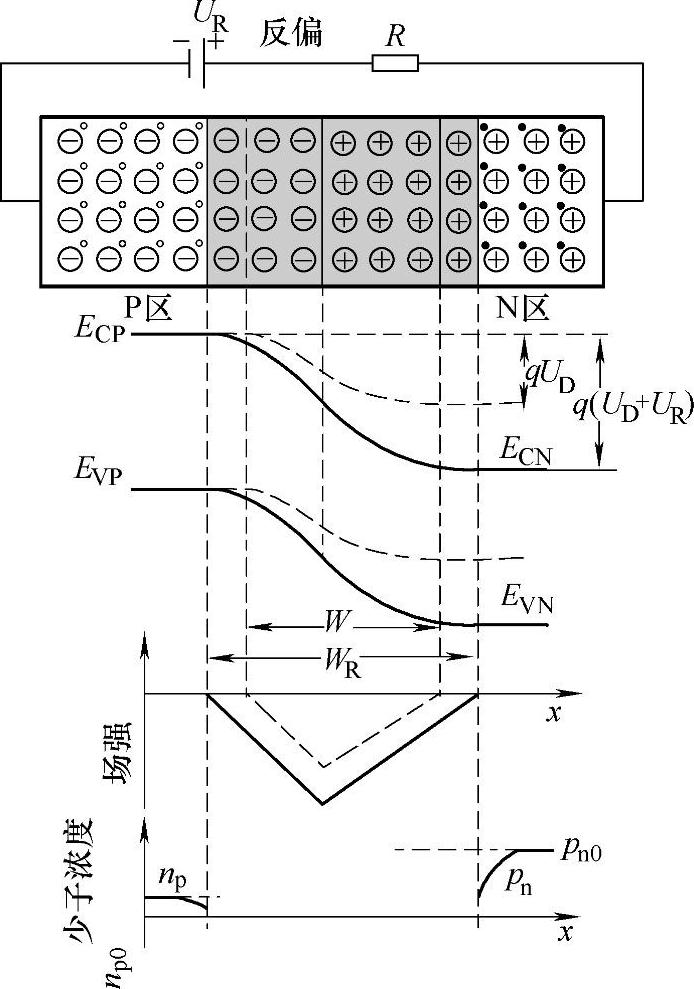
图3-11 反向偏置的PN的示意图

图中，由于空间电荷区的电场增强，强化了载流子的漂移运动，通过PN结的净电流是漂移电流而非扩散电流。此时N区边界处的空穴将被空间电荷区的强电场推向P区，P区边界处的电子将被同一电场推向N区，即P区和N区的少子被电场抽出，推向对面的区域。这个现象称为PN结的反向抽出效应，或者“少子抽出”效应。

这些少数载流子被电场推走之后，中性区内的少数载流子就要通过扩散流向边界，从而形成与加正偏压时的电流方向相反的电流，即反向电流。与正向电流不同的是，反向电流的形成不靠少子注入而靠少子抽取。少子注入时，少子来源于对方的多子，可随正偏压的升高而增加。但是，抽出的对象则是对方的少子，其密度原本就低，不能随反偏压的上升而明显变化。因此，在反偏压下的电流大小主要的不是看反偏压有多高，而是看构成反向电流的载流子来源到底有多丰富。由于受少数载流子密度太低的限制，PN结的反向电流很小，并且在一个较宽的电压变化范围内不随偏压的上升而增大，因而叫反向饱和电流。

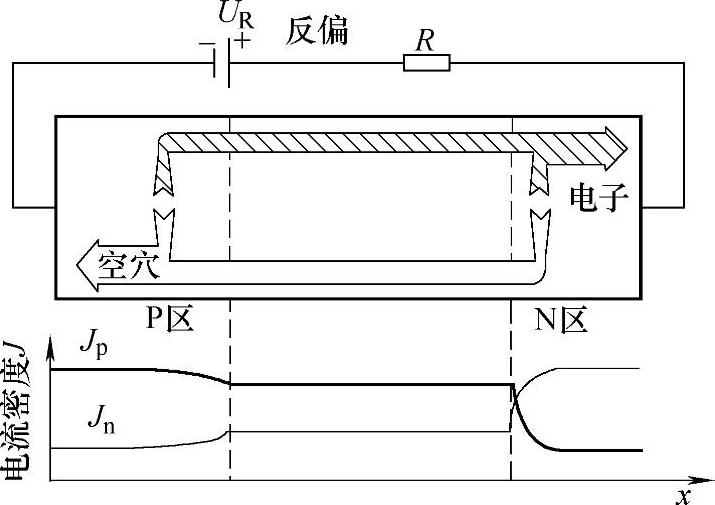
图3-12 反向偏置下PN结中电流的分布

图3-12给出了反偏置PN结中电流的分布。由于反向PN结具有抽出作用，使得被抽出少子区域的少子浓度低于平衡少子浓度，因而电离大于复合，即有电子空穴对的净产生。在N区净产生的空穴向PN结方向扩散，到达空间电荷区边界后，便被电场推过空间电荷区进入P区；而N区产生的电子，则以漂移的形式向右流出。同样在P区电离净产生的电子往PN结方向扩散，一到达空间电荷区边界，即被电场推过空间电荷区进入N区；产生的空穴，则以漂移的形式向左流。这样，就形成由N区流向P区的PN结反向电流，与正偏置PN结电流方向相反。PN结反向电流在N区的最右侧为电子漂移电流，在P区最左侧全部变为空穴电流，而在扩散区相互转化。

与PN结正向电流一样，反向电子电流与空穴电流的大小在PN结扩散区内各处是不相等的，但两者之和始终相等。采用类似的推导得出反偏置PN结中总的电流密度为

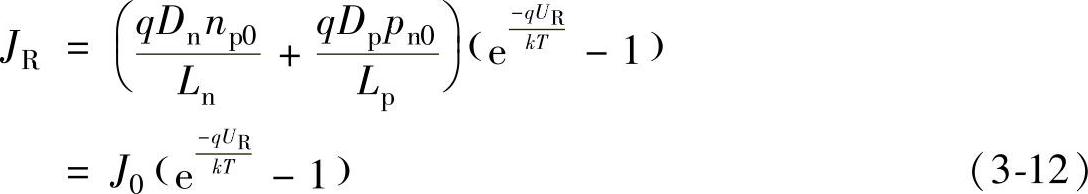
通常反向PN结外加反向偏压U_R的数值一般比kT/q大很多，即

J_R≈-J₀ （3-13）

这与上面分析的物理过程分析结果一致。

综合考虑正偏置和反偏置的PN结，统一考虑PN结的电压和电流的正方向，如图3-13所示，则可以得到无论正偏置还是反偏置，PN结中的电流密度和电压的关系表示为

这就是在若干假设条件下推导出的PN的伏安特性曲线，以U/（kT/q）和J/J₀为坐标做出的伏安特性如图3-14所示。可以看出PN结具有单向导电性，这是PN结最重要的性质之一。所谓单向导电性，就是当PN结的正向偏置时能通过较大电流，并且电流随着电压的增加而快速增大，表现为通态；反之，如果PN结反向偏置，则电流很小，而且电压增加时电流趋于“饱和”，表现为阻态。也可以说，PN结正向电阻小，反向电阻非常大。PN结的这种单向导电特性是由少子注入和少子抽取所决定的：少子注入使边界少数载流子浓度增加很大（几个数量级），从而形成大的浓度梯度和大的扩散电流，而且注入的少数载流子浓度随正向偏压增加成指数规律增加；而反向抽取使边界少数载流子浓度减少，边界处少子浓度的变化量最大不超过平衡时少子浓度。这就是PN结正向电流随电压很快增长而反向电流很快趋于饱和的物理原因。

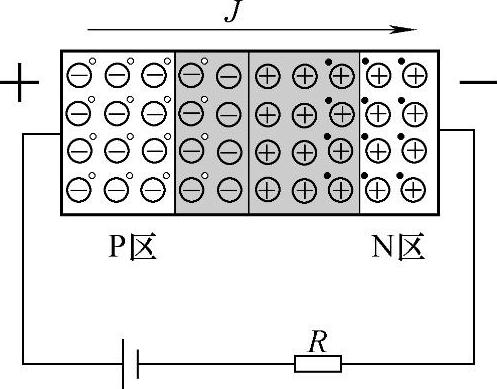
图3-13 PN结的电压、电流方向定义

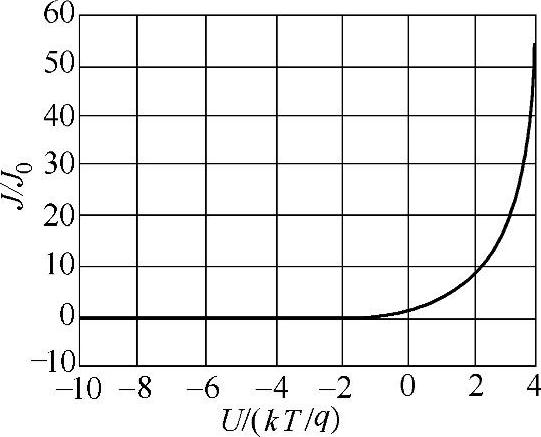
图3-14 理想状态下PN结的伏安特性