为便于说明问题，假定一个PN结是由原本分开的一块P型半导体和一块N型半导体紧密接触而成的，尽管在前面已强调指出这事实上不可能。在结合起来之前，P型半导体有高密度的空穴，而电子密度很小；相反，N型半导体的空穴密度很小，而电子密度甚高。重复上述内容，在P型半导体中空穴是多子，电子是少子；在N型半导体中，电子是多子，空穴是少子。当两者紧密结合在一起时，由于接触面上两种载流子的浓度梯度都很高。多子就要向对面的区域做扩散运动，即N区中的电子要向P区扩散，P区中的空穴要向N区扩散。对于P区，空穴离开后，留下了不可移动的带负电荷的电离受主，这些电离受主在PN结的P区侧形成了一个负电荷区；同样，在N区由于走失电子而出现了由不可移动的电离施主构成的正电荷区，这个交界区域就是PN结。

空间电荷区中的这些电荷产生了从N区指向P区，即从正电荷指向负电荷的电场，称之为自建电场。自建电场同样会使其作用范围内的自由电子和空穴作漂移运动，但其方向恰与其各自的扩散方向相反，即自建电场起阻滞电子和空穴继续扩散的作用。随着载流子扩散的进行，空间电荷逐渐增多，空间电荷区逐渐扩展，同时，自建电场也逐渐增强，载流子的漂移逐渐加强。在无外加电压的情况下，载流子的扩散和漂移将最终达到动态平衡，即两种载流子的扩散电流和漂移电流各自大小相等、方向相反，因此没有净电流流过PN结。这时，空间电荷的数量一定，空间电荷区不再继续扩展而保持一定的宽度和一定的自建电场强度。这就是平衡条件下的PN结。此时，载流子的扩散和漂移虽未停止，但已达到动态平衡。图3-4a和b分别给出PN结发生前后的共价键示意图。为了更具有一般性，图中P区和N区的掺杂浓度不相等，P区的掺杂浓度大于N区的。

在平衡条件下的PN结空间电荷区域内，由于空间电荷区中载流子已扩散殆尽，因而这个区域中的载流子浓度比P区和N区的多数载流子浓度低得多，像是被消耗尽了一样。因此，空间电荷区又称为耗尽层。另一方面，由于内电场对载流子的扩散运动具有阻挡作用，使载流子的扩散能力降低，所以空间电荷区又称为阻挡层。

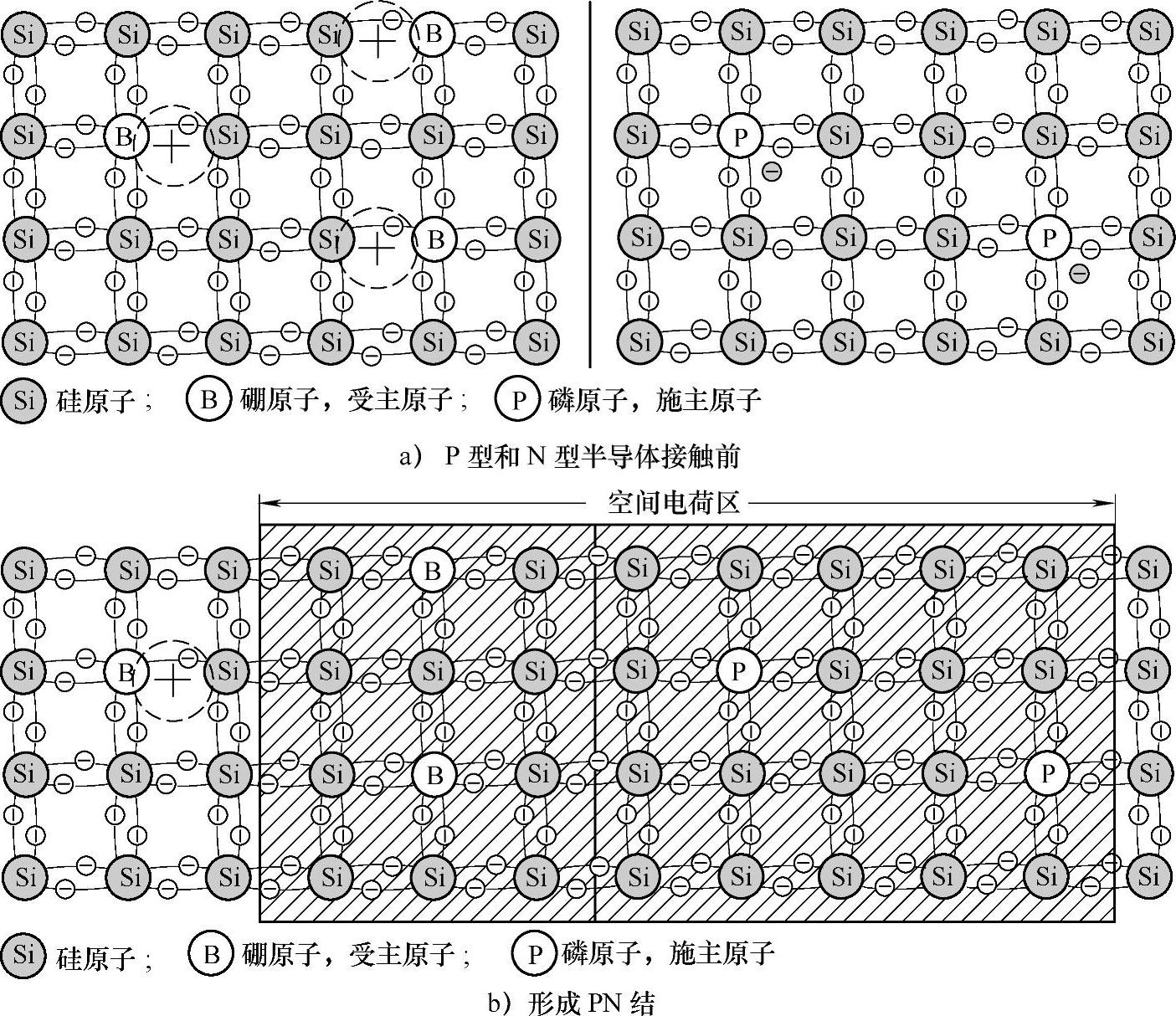
图3-4 PN结发生前后的共价键示意图

PN结空间电荷区及其自建电场的建立，反映在载流子的能量关系上就是如图3-5所示的能带弯曲。图3-5a表示结合前P型和N型半导体各自的能带图，E_C和E_V分别表示导带底和价带顶，即半导体中自由电子和自由空穴的能量位置；E_FP和E_FN分别表示P型和N型半导体的费米能级。费米能级是半导体导电类型和载流子密度高低的标志。费米能级离导带近者为N型，距离越短，自由电子密度越高；反之为P型，并且离价带越近自由空穴密度越高。图中E_FP至价带的距离比E_FN至导带的距离短，说明该P型半导体的空穴密度比该N型半导体的电子密度高，与图3-4的情况相对应。由于两块半导体的费米能级是不相等的，当两块半导体接触时电子要从费米能级高的N区流向费米能级低的P区，P区的电子逐步增多，其费米能级连同整个P型半导体的能带逐步升高。当两个费米能级调到同一水平位置时，即E_FP=E_FN时，电子不再流动，整个半导体宏观上没有电流流动，即达到PN平衡，此时PN结就有了一个统一的费米能级，如图3-5b所示。换句话说，在热平衡没有电流流动的半导体内，费米能级是处处相等的，这是半导体领域中一个比较重要的结论。

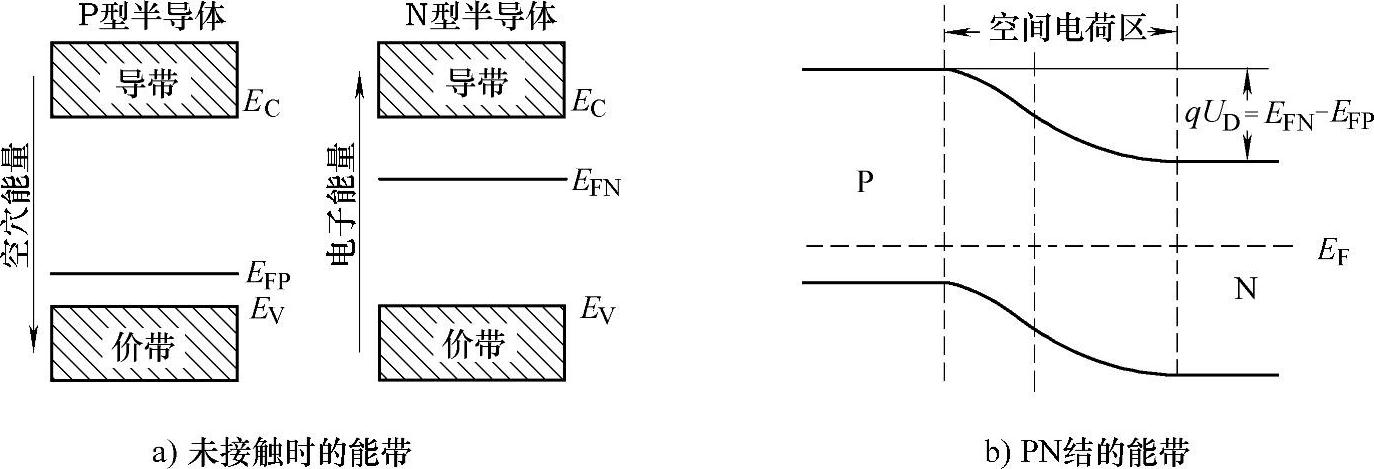
图3-5 PN形成的能带示意图

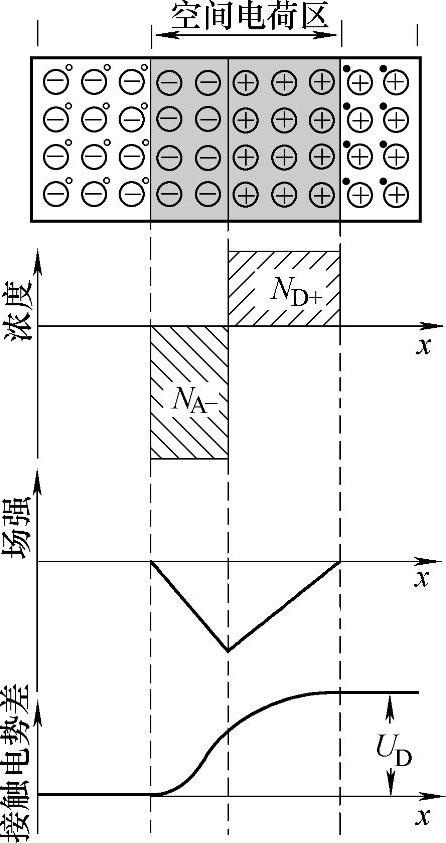
图3-6 空间电荷区内离子浓度、 电场和电势的分布示意图

由图3-5可知，空间电荷区内能带因自建电场的建立而弯曲，其中费米能级与导带底或价带顶的距离不再像空间电荷区外那样处处相等。由于自建电场从N区指向P区，空间电荷区内电势由N区向P区降低，电子的电势能由N区向P区升高，也即P区能带相对N区上移。能带弯曲给N区电子设置了一个阻挡其向高势能P区运动的障碍，称为势垒；同样，空穴也有一个阻挡其从P区向N区运动的势垒。势垒高度qU_D，就是费米能级移动的距离，即qU_D=E_FN-E_FP。U_D是势垒两边电子的电势能之差，是因接触而产生的，因而称为接触电势差。

若杂质是均匀分布的，图3-6给出了空间电荷区内离子浓度、电场和电势的分布示意图，图中从离子浓度分布到电场分布的关系为泊松方程，而电场的积分，即三角形的面积就是接触电势差，由此图中的相互关系，可以求出图中的各个特征量，比如空间电荷区的宽度、最大电场强度等，在此仅给出接触电势差的结果，其他不再赘述。从上一章可以知道，在N型半导体中

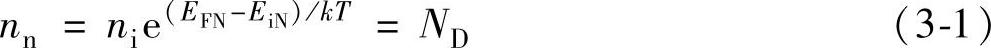
在P型半导体中

由此可以求出

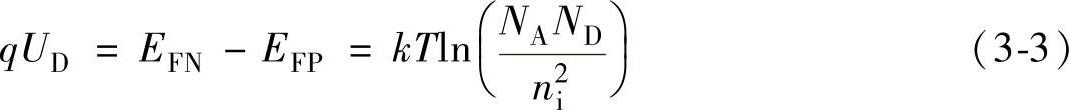(www.daowen.com)

即

式中 N_A、N_D——P型和N型净杂质的浓度；

n_i——本征载流子浓度；

k——玻尔兹曼常数；

T——绝对温度；

q——电子电荷量。

室温下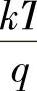

约为0.026V。可以看出，U_D跟PN结两侧的掺杂浓度、温度、材料的禁带宽度（体现在材料的本征载流子浓度n_i上）有关。在一定温度下，N区和P区的净杂质浓度越大，即N区和P区的电阻率越低，接触电势差越大；禁带宽度越大，n_i越小，U_D也越大。若N_A=10¹⁷ cm^-3，而N_D=10¹⁵ cm^-3，则在室温下可以计算得到硅的U_D=0.7V。另外还可看出，随着PN结温度的升高和本征载流子浓度n_i的增大，U_D将减小。

通过推导和整理，可以得到空间电荷区的宽度为

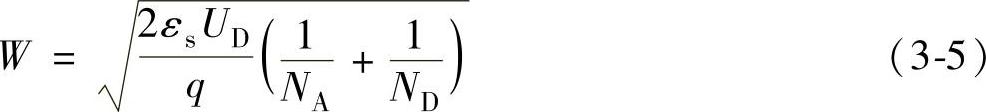
式中 ε_s——半导体材料的介电常数。

从图中可以看出，低掺杂的N区空间电荷区宽度大，当P区和N区的掺杂浓度相差比较远的时候，整个空间电荷区的宽度主要取决于低掺杂浓度，上面的公式也说明了此问题。同时，随着PN结温度的升高，U_D将减小，则空间电荷区的宽度也减小。另外，此公式在讨论PN结偏置中仍有重要作用。

图3-7中给出了平衡条件下PN结的载流子浓度分布，其中在N区和P区的中性区（即没有电场的区域），载流子的浓度分布是均匀的。可以这样理解，在此两个区域内，没有电场作用下的载流子做漂移运动，而半导体的宏观电流为零，所以就不存在因为浓度不同而产生的扩散电流，即浓度均匀。而在空间电荷区，可以认为其是耗尽区，不考虑载流子浓度分布。

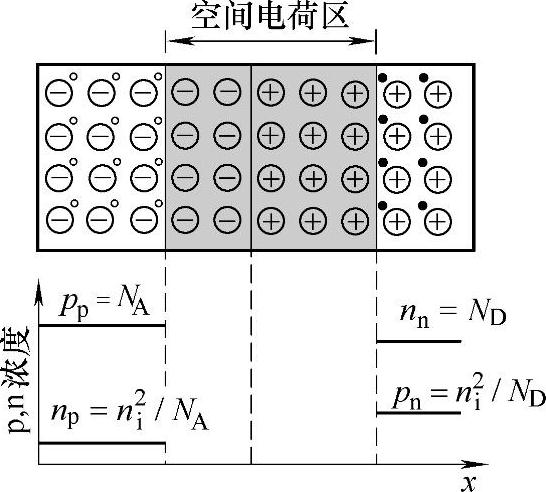
图3-7 平衡条件下PN结 的载流子浓度分布