在了解了N型和P型半导体形成过程的基础上，可以对杂质半导体中的一些关键参数进行分析。

首先，可以分析杂质半导体中载流子的浓度，即电子和空穴的浓度。不失一般性，以同时掺入施主和受主的上例来说明。假设在半导体中掺入的施主原子浓度为N_D，掺入的受主原子浓度为N_A。在一定温度下，施主和受主都被完全地电离，则电离后留下浓度为N_D带正电的施主离子和浓度为N_A带负电的受主离子。半导体中产生的电子和空穴的浓度分别为n和p，在整体带电量为零的半导体中，正电荷和负电荷浓度相等，则有

p+N_D=n+N_A （2-27）

同时考虑能量作用定律

pn=n²_i （2-28）

上述公式中，N_A和N_D为已知量，两式联合求解，会变成二次方程，为得到符合实际情况的正解根，分两种情况分析，分别对应N型和P型半导体。

1）N型半导体，即N_D>N_A，为表述清楚，使用n_n和p_n来表示N型半导体中的电子和空穴浓度，角标n即意味着在N型半导体中。则可求出

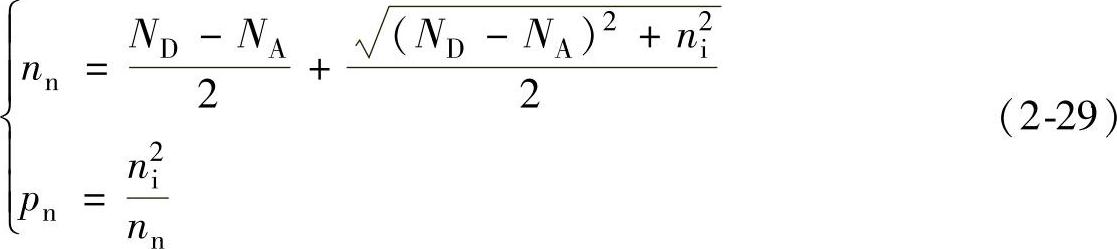
2）P型半导体，即N_A>N_D，同样，使用n_p和p_p来表示P型半导体中的电子和空穴浓度，角标p即意味着在P型半导体中。则可求出

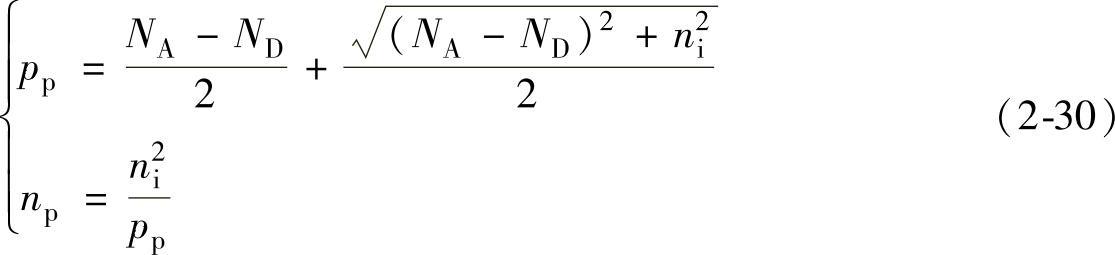
通常，半导体中的纯载流子浓度|N_D-N_A|比本征载流子浓度n_i大得多，则上述公式可以简化，以N型半导体为例。

对于N型半导体，若无受主原子掺入，仅有施主原子，则为

对于P型半导体的简化结果也可以类似推出。

上述结果也表明，在N型半导体中，电子的浓度远大于本征载流子浓度，而空穴的浓度小于本征载流子浓度，电子占绝对多数，称为多数载流子，简称多子，而空穴为少数载流子，简称少子。在P型半导体中，空穴的浓度远大于本征载流子浓度，而电子的浓度小于本征载流子浓度，空穴为多子，电子为少子。

做如下一个简单的估算：本征硅在室温下的载流子浓度n_i是10¹⁰/cm³数量级，若掺入极少的杂质，如杂质原子与硅原子的比例是1/10⁶，根据硅晶体中硅原子数是10²²/cm³数量级，可知掺入的杂质浓度就是10²²×10^-6/cm³=10¹⁶/cm³。若完全电离，载流子浓度等于杂质浓度，则即掺入百万分之一的杂质，结果载流子浓度增加一百万倍。

其次，可以分析杂质半导体中的费米能级，这对后面章节电力半导体器件的分析非常重要。在N型半导体中，施主原子完全电离时，电子浓度几乎等于施主原子的浓度，同时考虑由费米-狄拉克分布函数得到的电子浓度公式则有

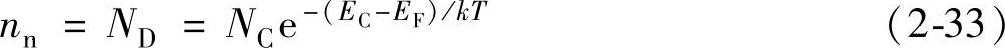
可以求出(www.daowen.com)

同样的在P型半导体中可以求出

明显地，在N型半导体中，当施主浓度N_D越大，导带底部与费米能级间的能量差E_C-E_F就越小，即费米能级就越接近导带底部；在P型半导体中，当受主浓度N_A越大，其费米能级与价带顶部的能量差E_F-E_V就越小，即费米能级就越接近价带顶部。为了直观表述，图2-33a～e分别给出不同杂质半导体与本征半导体费米能级的对比。

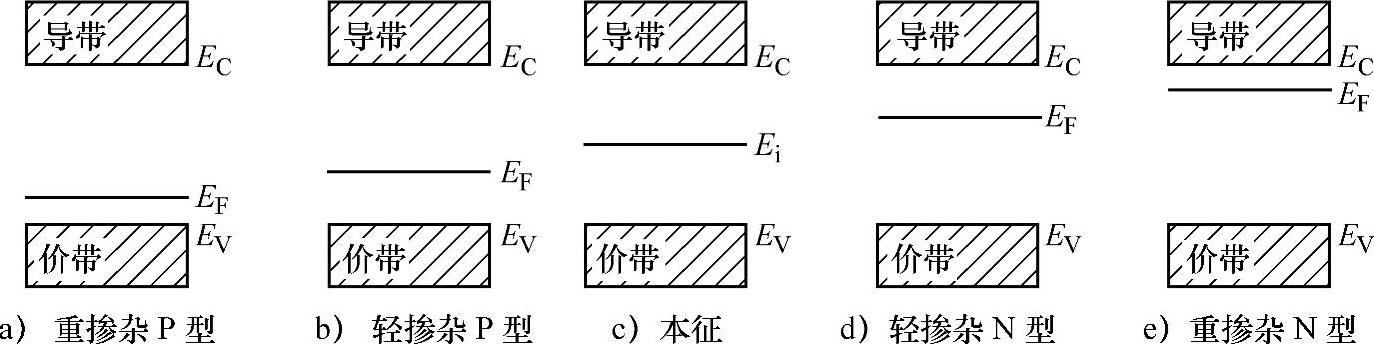
图2-33 不同杂质半导体与本征半导体费米能级对比

可以看出，在杂质半导体中，费米能级表征了半导体内载流子的浓度。对于杂质半导体的费米能级，仍需强调以下几点：

1）所谓的费米能级，其实并不是真正的电子的能级，在半导体的能带中不一定存在一个与费米能级数值相等的能态来允许电子占据，它只是各能级上电子或者空穴统计分布的一个参量。粗略地说，凡是费米能级以上的能态基本都是空的，即没有电子或者很少的电子占据这些能级；而费米能级以下的能态基本上都是填满电子的。图2-33中不同的费米能级的高低可非常直观地展示半导体中电子填充能力“水平”的高低。

2）费米能级在能带中的位置可以决定导体中两种载流子的比例。在本征半导体中，费米能级位于禁带的中间，电子与空穴浓度之比等于1；在P型半导体中，费米能级位于禁带中间以下的位置，电子与空穴浓度之比小于1，费米能级越低，该比值越小；在N型半导体中，费米能级为与禁带中间以上的位置，电子与空穴浓度之比大于1，费米能级越高，该比值越大。

3）从另一个角度看，费米能级也体现了半导体中的掺杂程度，受主原子掺杂越多，费米能级就越低，越向价带接近；施主原子掺杂越多，费米能级就越高，越向导带接近。

最后，再来看看上述分析中所做的一些假设，这些假设都与温度存在一定的关系。一个是在简化半导体中载流子浓度结果，使用了半导体中的纯载流子浓度|N_D-N_A|比本征载流子浓度n_i大得多的假设。实际上，随着半导体材料温度的不断升高，材料中硅的价电子能获得的热能不断增加，本征载流子浓度也在不断增加，当增加到一定程度，上述的假设不再满足，此时硅半导体中的电子的浓度不再近似等于|N_D-N_A|。图2-34中，给出了N型半导体中不同N_D-N_A差值下，电子浓度随温度变化而变化的情况。

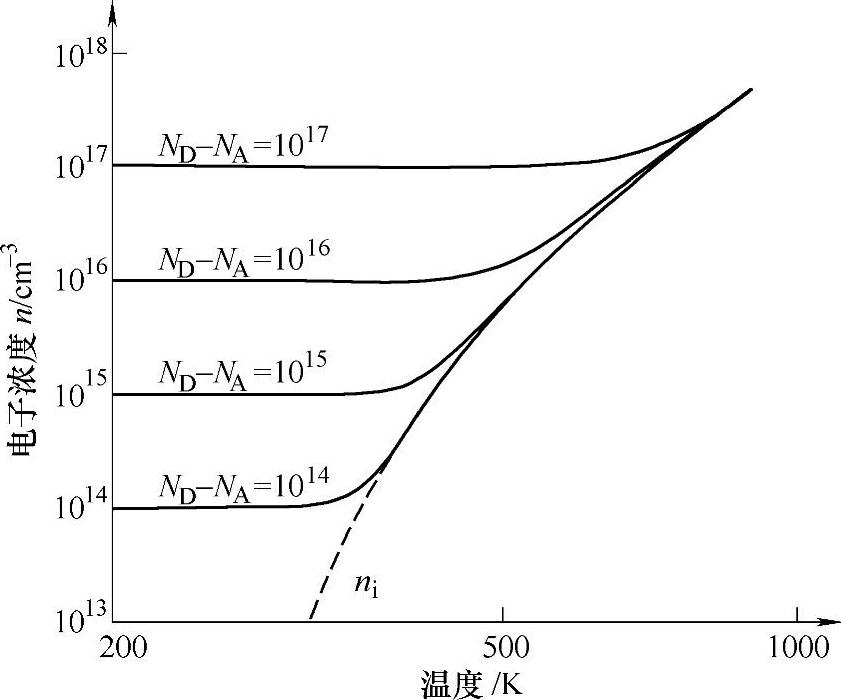
图2-34 电子浓度随温度变化而变化的情况

另一个假设是认为半导体中的施主或受主原子完全被电离。实际上，在很低的温度条件下，电子被施主原子或空穴被受主原子所约束而没有被电离，称作载流子被冻结。杂质原子不能完全电离，会很明显地影响半导体中的载流子的浓度。在图2-35中给出了一个N型半导体在从低温到高温时电子浓度的变化。

图中，在很宽的温度范围内，电子浓度与掺杂原子浓度相等，这个范围被称为工作区。在高温条件下，本征载流子浓度很快地增加，最后超过掺杂原子浓度。在这个温度以上，半导体是本征的。图2-34已经说明，随着掺杂原子浓度的降低，本征温度也会降低。

当半导体温度高于本征温度时，掺杂原子对载流子浓度没有影响，所以该温度对于半导体材料构成的器件非常重要，但是本征温度并不是半导体器件的最高工作温度。这与电力半导体器件的设计关系十分密切。比如电力半导体为了提高耐压，总是需要一个有很低掺杂浓度的区域，通常该区域对应的本征温度不等于器件最高工作温度。一般来说，当一个器件开始出现半导体基本组成部件不能实现它的功能时，就达到了最高工作温度。

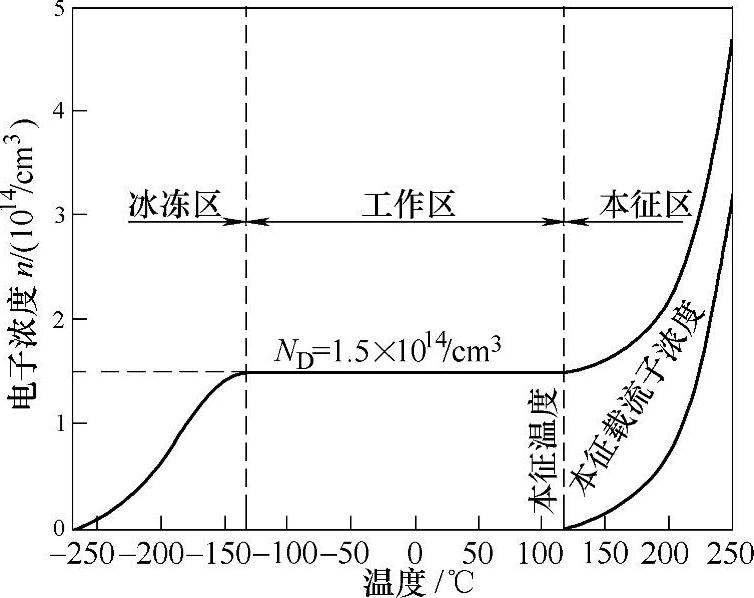
图2-35 N型半导体电子浓度 随温度变化示意图