在实际应用中，不可能像上述一样考虑单个导带中的电子和价带中的空穴对半导体导电行为的作用，在半导体中两种载流子的数目相对于硅原子数目来说是较少的，但也是一个庞大的数字，实际中不可能也没有意义去追踪单个电子或者空穴的运动对半导体导电的影响。所以将半导体作为一个整体来考虑其导电行为，此时就需要知道两种载流子的浓度，一般使用n和p来表示。从图2-24中可以看出，电子具有电子寿命，此时就不可避免要使用统计力学中的能量状态分布概率函数来决定载流子的分布情况。

在晶体中，电子的能量状态分布遵循所谓的费米-狄拉克（Femi-Dirac）分布函数，即

式中 k——玻尔兹曼常数，k=1.38×10^-23J/K；

T——绝对温度；

E_F——一个能量参考值，叫做费米能量或者费米能级。

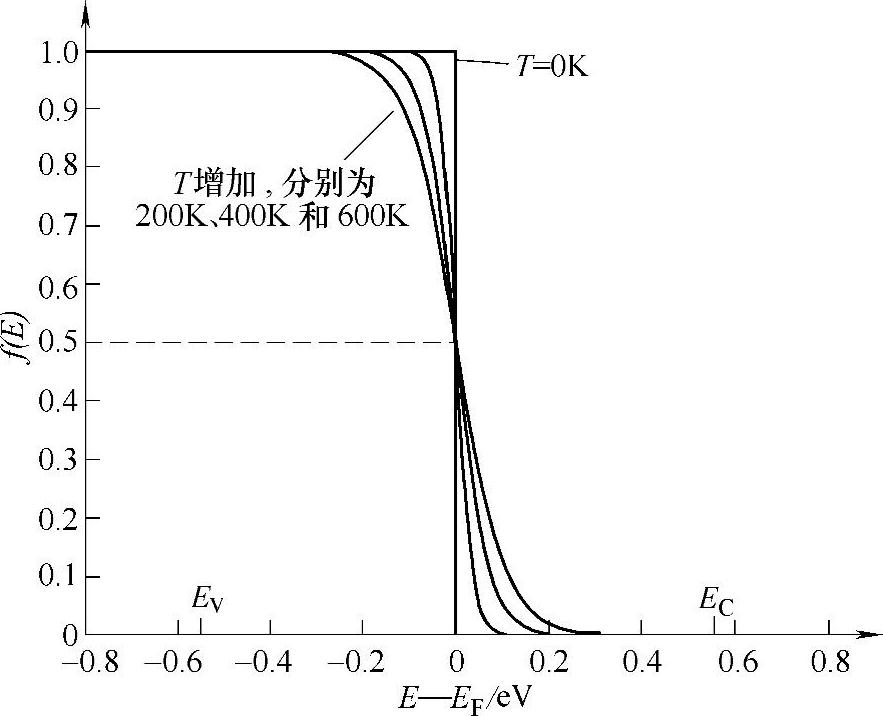
图2-25 不同温度下费米-狄拉克分布

该式表示一个电子占据能量为E状态的概率，图2-25给出了不同温度下费米-狄拉克分布函数的值。图中可以看出，在T=0K的时候，当E<E_F时，f（E）=1，而当E>E_F时，f（E）=0，即在绝对零度时，电子都是位于它们尽可能低的能态上，都处于价带上，而导带上是空的。而当温度大于绝对零度时，在费米能级E_F上被电子占据的概率刚好等于0.5，而高于E_F的能态被电子占据的概率不再等于零，而低于E_F的能态上总是有一些是空的（概率小于1）。这就意味随着半导体温度的升高，电子获得动能的增加，将从价带电离到导带上，为了有直观的概念，图中也标注了纯净的硅的价带上边界E_V和导带的下边界E_C。有趣的是，虽然在费米能级处，该能级被占据的几率为0.5，但是事实上，那里是没有被允许的能态的。

费米-狄拉克分布函数有一个更简单的描述来近似，当能量与E_F相差3kT以上时，有

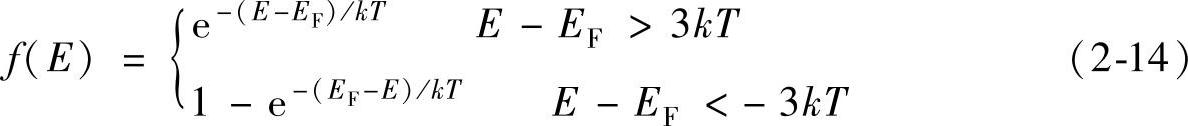
这就是费米-狄拉克分布函数的玻尔兹曼近似，或者叫做费米-狄拉克概率函数，在室温下，即T=300K时，1kT=0.026eV，这是一个经常用到的数据。

注意到这样一个事实，f（E）表示一个电子占据能量为E状态的概率，则1-f（E）为空穴占据能量为E状态的概率，因为在一个能态上不是被电子占据，就是被空穴“占据”。则式（2-14）可写为

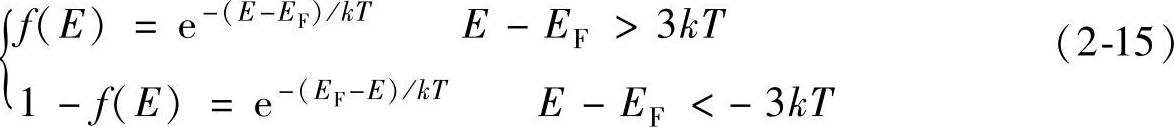(www.daowen.com)

即在低于E_F的某个能态E上，空穴占据的概率为e^{-（EF-E）/kT}；而在高于E_F的某个能态E上，电子占据的概率为e^{-（E-EF）/kT}，这样更方便记忆。

从图2-25中可以看到，随着温度的升高，导带中一个给定能态被占据的几率随之增大。同样地，价带中一个给定能态被占据的几率随之减小。这意味着温度越高，可以携带电流的电子和空穴就越多。可以做一个简单的计算，室温下硅的禁带宽度为1.12eV，若电子位于导带底部，即E=E_C。对于纯净的硅材料，费米能级近似位于禁带中央位置，因此，E-E_F=0.56eV，则有以下计算结果

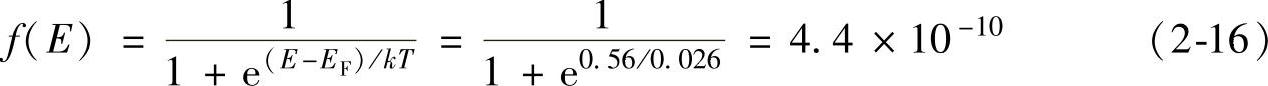
也就是说，在室温下大约20亿个能态中才有一个被占据，而绝不像图2-24那样多。

利用费米-狄拉克分布函数，可以来计算导带中的电子浓度为

式中 E_C——导带的下边界；

N_C——导带中有效态密度，其具体推导在此不详细给出。

在室温下，硅的N_C=2.8×10⁹/cm³=2.8×10¹⁵/m³，同样的价带中的空穴浓度为

式中 E_V——价带的下边界；

N_V——价带中的有效态密度。