首先，回顾一下孤立原子中的电子状态，这其中也经历了不同阶段的认识过程。在20世纪初，科学家们致力于发展和建立物理模型，来解释观察到的实验结果，如X射线散射、光电效应、原子的发射和吸收谱等。1897年，J.J.Thomson（汤姆逊）发现了电子，并推断原子是由正电荷和负电荷组成的，随后提出了一种原子模型，认为电子镶嵌在均匀分布的正电荷的球中，如图2-2a所示。1911年，Ernest Rutherford（卢瑟福）在一项α粒子散射实验中发现，原子的正电荷集中在一个非常小的核中，核的大小是原子的万分之一。他正确地对汤姆逊的模型进行了改进。在卢瑟福的原子结构模型中，假设所有正电荷和原子全部的质量几乎都集中在原子中央很小的区域内。这个核心区域常被当作是半径为10^-14m量级的圆球来处理。假设带有负电荷的电子绕着带有正电荷的核的轨道运动，就像是行星绕着太阳运动或者卫星绕着地球运动。1913年，Neils Bohr（玻尔）假设卢瑟福模型中的电子以圆形轨道绕核运动，如图2-2b所示。按照这个假设，如果要保持原子的稳定，电子的能量只能取某些特定值，或者说，能量必须是量子化的。能量和许多其他的可观测量（可以直接测量得到的物理量）都可以用普朗克常量来表示。玻尔预测的原子中电子的能量和根据光谱数据得到的实验结果符合得非常好。在1916年，Wilson-Sommerfeld（威尔逊-索末菲）将玻尔的模型推广，使之适用于任何粒子作周期性运动的物理体系中。改进的模型允许电子按照椭圆形轨道运动。

这里有必要说明一下氢原子的玻尔模型，因为在半导体器件中，类氢杂质是很重要的，而这些杂质可以用类似玻尔模型的方法来处理。在氢原子的玻尔模型中，电子按圆形轨道绕核旋转。由于原子核的质量为1.67×10^-27kg，是电子质量的1830倍，因此可以认为原子核在空间是固定不动的。以中性氢原子为例，它拥有一个轨道电子，把原子核和电子都作为点电荷来处理。带负电荷-q_e的电子和带正电荷的原子核+q_n之间的库仑力为

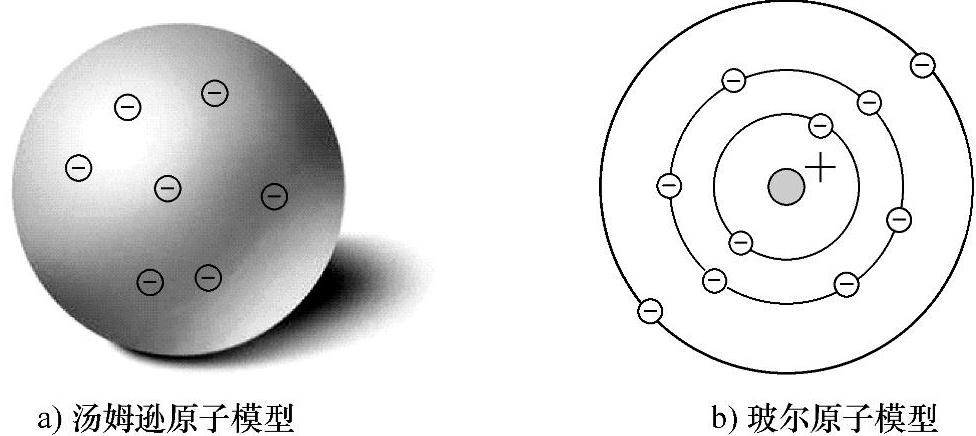
图2-2 两种不同的原子模型

式中 r——两点电荷之间的距离；

ε₀——真空的介电常数，ε₀=8.85×10^-12F/m；

q_e、q_n——电子、原子核电荷量，均为1.6×10^-19C。

式（2-1）中的负号表明两者是吸引的。可以对于上式进行势能计算，注意到无穷远处的库仑力为零，因此选择无穷远处作为势能参考点是很方便的。定义无穷远处的势能为真空能级，其具有的意义为：把一个电子从原子核的束缚下变成自由电子需要的能量，也就是把电子移动到无穷远处需要的能量。如果电子离原子核无穷远，实际上就已经不属于原子的一部分，而成为真空中的自由电子了。为了表述上的方便，不妨将真空能级所具有的势能认为是零，则距离原子核r的电子的势能可以表示为

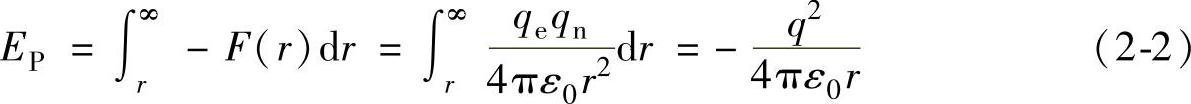
电子的势能E_P与r的关系可以画成图2-3所示的氢原子模型。可以明显看出，在图2-3所示的势阱中，电子处于底部的势能不能被赋为零参考值，即当距离r接近零时，电子和原子核正电荷之间的吸引力就会急剧上升而发散，所以这样的势阱的深度是无限的。

由于电子以半径为r的圆绕核旋转，从牛顿力学可知，离心力为

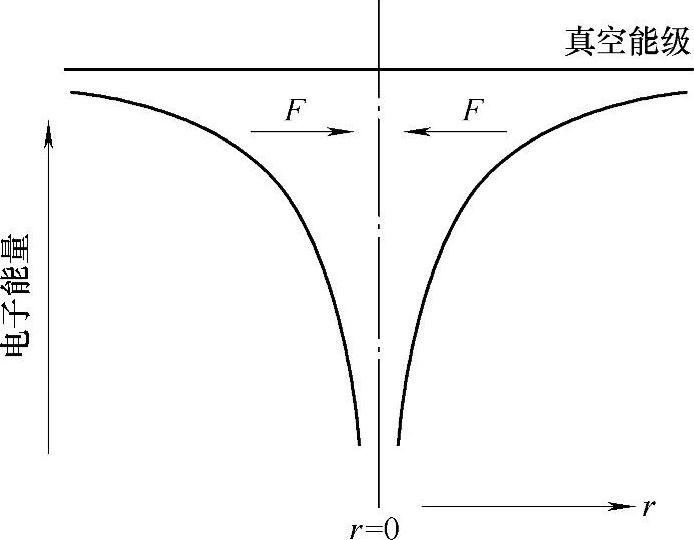
图2-3 氢原子中电子的势能模型

为了使原子保持稳定，电子受到的净作用力应该为零，则作用在电子上的离心力和向心力（即库仑力）相等，有

在玻尔模型中，还假设沿封闭轨道的角动量的积分应该等于普朗克常量的整数倍，即

式中 n——整数。

由于玻尔模型中的轨道是圆形的，对于一个确定的r，势能E和速度v也是确定的，则有(www.daowen.com)

2πmvr=nh （2-6）

根据上面的公式，对应n的每一个正整数，都能求出r和v的解，此时n被称作量子数。

氢原子中的电子的能量（或者说能级）为电子的势能与动能之和（单位为eV），即

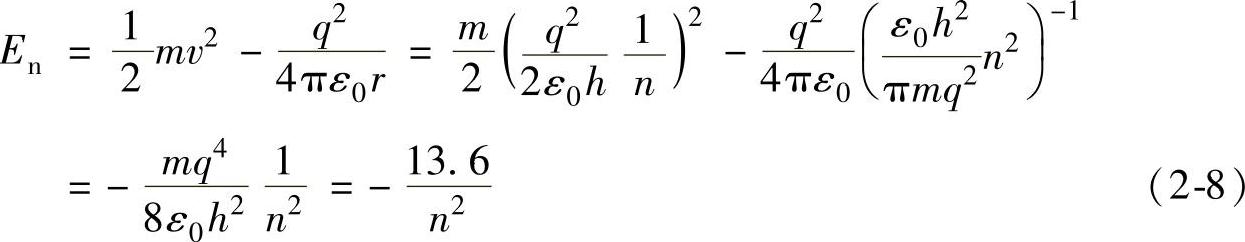
式中 m——电子的自由质量，m=9.11×10^-31kg；

q——基本电荷，q=1.6×10^-19C；

ε₀——真空介电常数，ε₀=8.85×10^-12F/m；

h——普朗克常量，h=6.63×10^-34J·s。

在这里使用了eV（电子伏特）作为能量单位，它可以定义为一个电子被1V的电势差加速所获得的能量。这与电力电子领域中常用的能量电位J（焦耳，W·s）有定量的关系，即

1eV=1.6×10^-19J

则有氢原子玻尔模型中的电子运动轨道半径（单位为nm）为

得到的氢原子中的电子的能级和轨道见表2-2，为了直观表示，将这些能级与轨道半径画成图2-4a、b所示。从图中可以看出，真空能级和允许能量之间的差值是按照1/n²的规律变化的。即量子数越大，能级（的能量）就越接近。同时，玻尔模型中电子轨道半径是按照n²的规律变化的，即能级越高，电子距离原子核越远。如果电子的能量高于真空能级，原子核与电子之间的库仑力就不足以将电子束缚在原子核的周围。另外，虽然可能的状态数是无限多的，但是一旦一个电子占据了其中的一个状态，氢原子就成为中性的，不会再吸引其他电子了。

表2-2 氢原子中电子能级及轨道半径

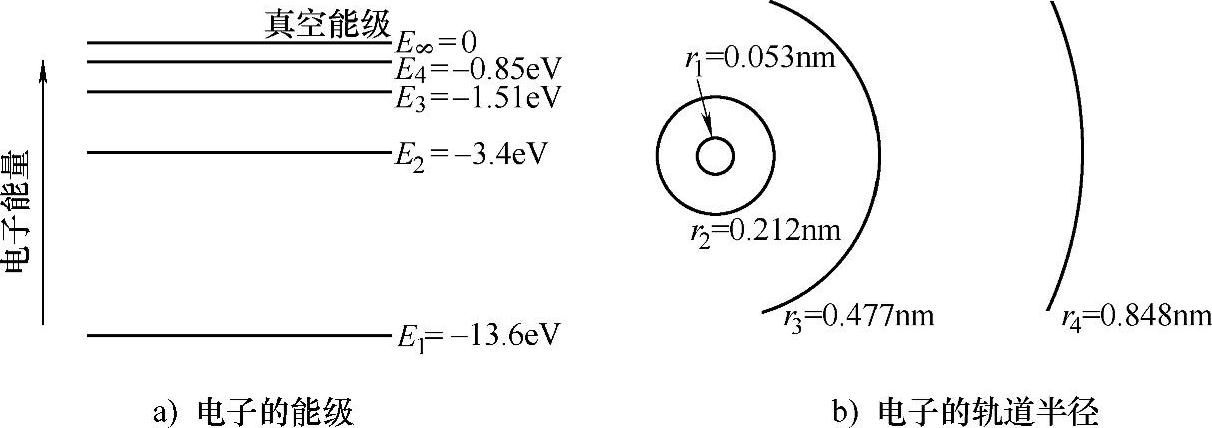
图2-4 氢原子玻尔模型中的电子能级和轨道半径

以上的这些分析可以用于描述原子核中含有更多电荷的更复杂的原子，所不同的是图2-3所示的势能陷阱的形状有所不同，当n=1时，电子的能级和轨道半径的数值有所不同，但其能级的变化以及轨道半径的变化仍然是按照上述的规律分布的。这里的n是量子数，准确地说是主要量子数，也可理解成为是层序号。层被分为了子层，显示了电子的不同角动量。子层数，也被称为角动量量子数l。子层一般使用字母s、p、d、f等来表示。由于原子中电子的相互作用，子层的能级有着微小的区别。在原子模型中，一般还会使用到另外两个的量子数，即磁量子数和旋转量子数。对于本书所进行的物理基础分析，这两个量子数暂时不需要。