1.蜗杆传动的特点

（1）蜗杆传动的主要优点

1）传动比大。蜗杆传动单级传动比大，例如机床的分度机构传动比可达1000，因此，可实现大的减速、大的增大转矩的作用。

2）结构紧凑。在实现同样传动比的情况下，是结构最紧凑的传动件。

3）传动平稳、噪声小。由于蜗杆轮齿是连续不断的螺旋齿，它与蜗轮轮齿的是逐渐进入啮合、逐渐脱离啮合，故传动平稳、噪声小。

4）自锁性好。当蜗杆的导程角小于当量摩擦角时，可实现反向自锁，即具有自锁性。

（2）蜗杆传动的主要缺点

1）效率低。因为传动时啮合齿面间相对滑动速度大，故摩擦损失大，效率低。所以在传动设计时需要考虑散热问题；蜗杆传动不宜用于大功率传动（尤其在大传动比时）。

2）成本高。为了减轻齿面的磨损及防止胶合，蜗轮一般使用贵重的减摩材料制造，故成本高。

3）精度要求较高。对制造和安装误差较为敏感，安装时对中心距的尺寸精度要求较高。

2.主要参数和几何尺寸计算

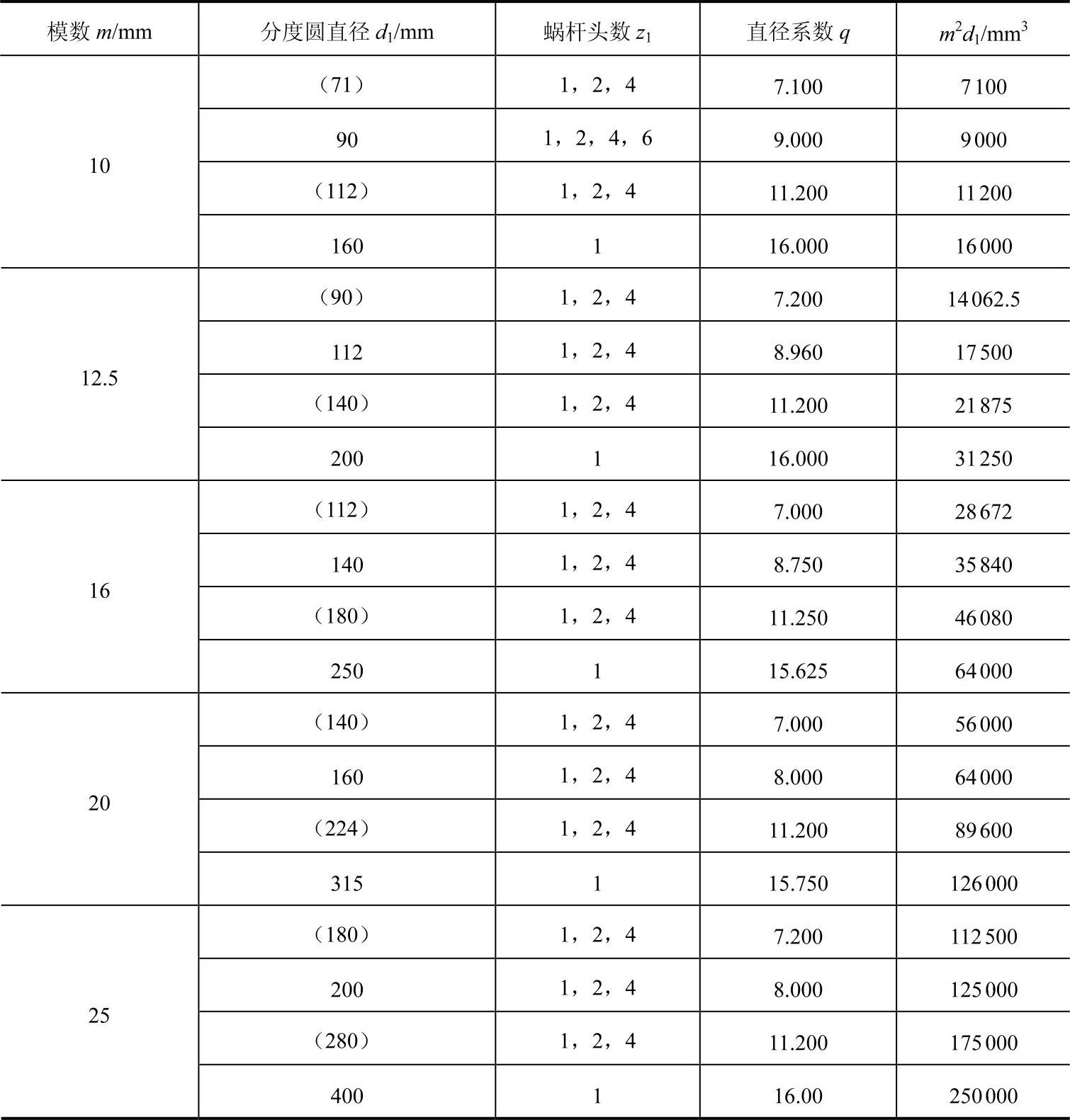
（1）主要参数 正确选择和匹配参数是圆柱蜗杆设计的首要任务，它直接关系到传动的承载能力和经济性。动力蜗杆传动（Σ=90º）蜗杆基本参数及其与蜗轮参数的匹配见表6-58。

1）模数m和压力角α。由蜗杆传动正确啮合条件可知，蜗杆的轴向模数和蜗轮的端面模数相等且均取为标准模数，即m_x=m_t=m，普通圆柱蜗杆传动的标准模数见表6-58。

阿基米德（ZA型）蜗杆的轴向压力角等于蜗轮的端面压力角，等于标准压力角，即α_x=α_t=20°。其他类型的蜗杆传动蜗杆的法向压力角为标准压力角，即α_n=20°；蜗杆的轴向压力角和法向压力角的关系为：。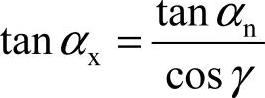

2）蜗杆分度圆直径d₁、蜗杆直径系数q、蜗轮分度圆直径d₂。在蜗杆传动中，为了保证蜗杆与配对的蜗轮正确啮合，常用与蜗杆具有相同尺寸的蜗轮滚刀来范成加工与其配对的蜗轮。这样，只要有一种尺寸的蜗杆，就需要有一种对应的蜗轮滚刀。对于同一模数，可以有很多不同直径的度圆直径的蜗杆，因而对每一模数就需要配备很多蜗轮滚刀，这样很不经济。为了限制蜗轮滚刀的数目及便于滚刀的标准化，就对每一标准模数规定了一定数量的蜗杆分度圆直径d₁。 蜗杆直径d₁与模数m的比值称为蜗杆的直径系数：。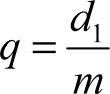

由于d₁与m值均为标准值，所以得出的q不一定是整数。

蜗轮分度圆直径的确定和齿轮的相同，即d₂=mz₂ 。

3）传动比i和齿数比u。

传动比：

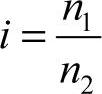
齿数比：

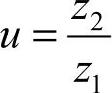
式中 n₁，n₂——蜗杆和蜗轮的转速；

z₁，z₂——蜗杆和蜗轮的齿数。

当蜗杆为主动时，传动比为：。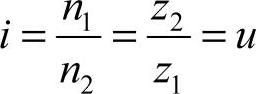

表6-58 普通圆柱蜗杆基本参数及其与蜗轮参数的匹配

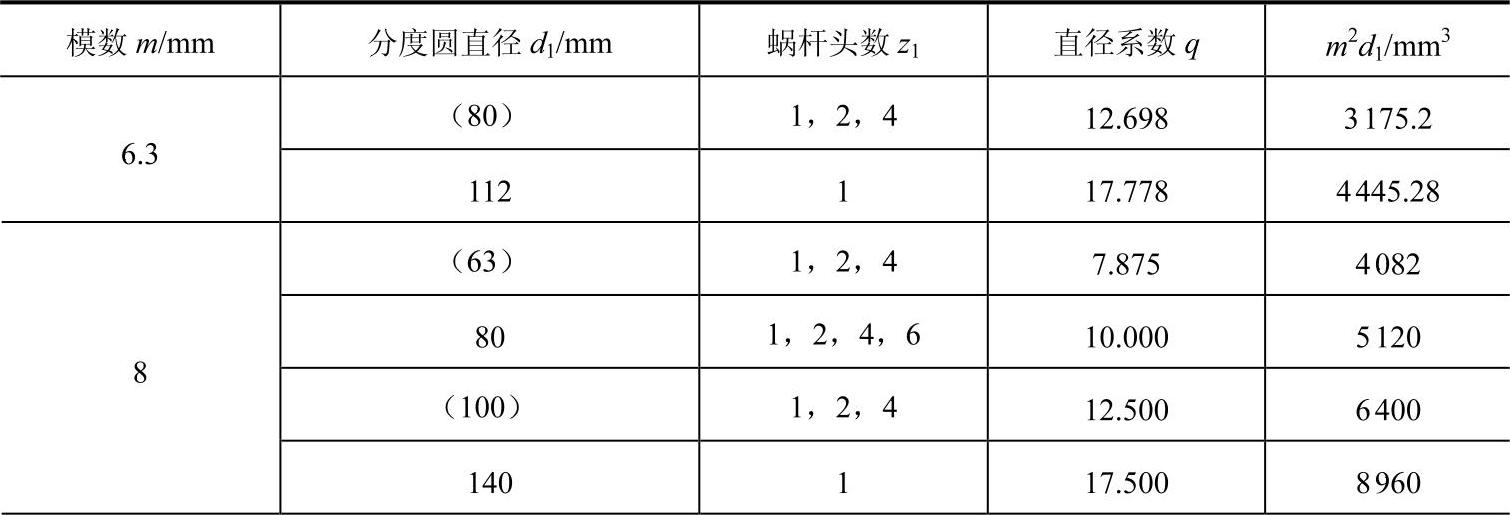
（续）

4）蜗杆分度圆上的导程角γ。将分度圆上的螺旋线展开（见图6-47），根据几何关系可知，蜗杆分度圆上的导程角γ由下式确定：

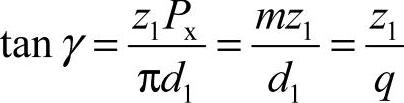
通常γ=3.5°～27°。

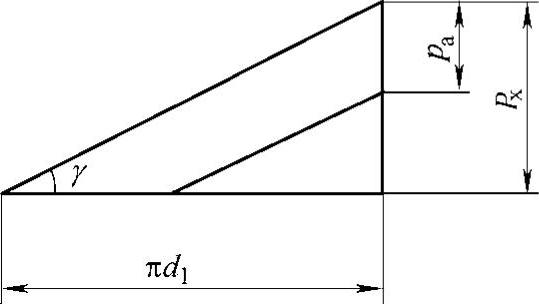
图6-47 蜗杆螺旋线的几何关系

5）蜗杆传动的滑动速度v_s。在蜗杆传动中，蜗杆与蜗轮的啮合齿面间会产生很大的齿向相对滑动速度v_s，如图6-48所示。因为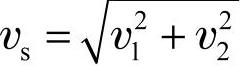，所以。

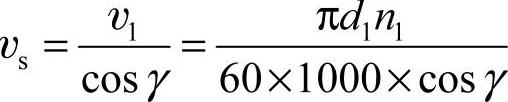6）蜗杆传动的啮合效率η₁。蜗杆传动类似于螺旋传动，当蜗杆主动时，其啮合效率为

式中 γ——蜗杆的导程角，它是影响啮合效率的主要因素；

ρ_v——当量摩擦角，ρ_v=arctanf_v。f_v为当量摩擦系数，其值取决于蜗杆、蜗轮的材料及滑动速度v_s，在润滑条件良好的情况下，v_s有助于润滑油膜的形成，从而降低f_v值，提高传动效率。f_v、ρ_v的值可查表6-59。

7）蜗杆传动的标准中心距a。蜗杆传动的标准中心距为

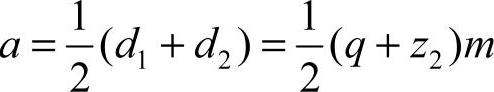
式中 d₁，d₂——蜗杆与蜗轮的分度圆直径；

q——蜗杆的直径系数；

z₂——蜗轮的齿数；

m——蜗杆传动的模数。

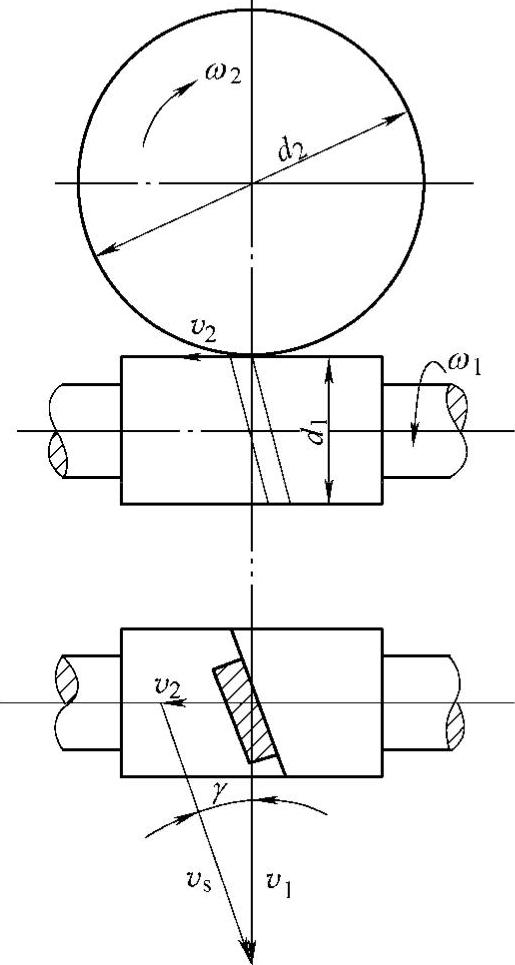
图6-48 蜗杆传动的滑动速度

表6-59 蜗杆传动的当量摩擦系数f_v和当量摩擦角ρv

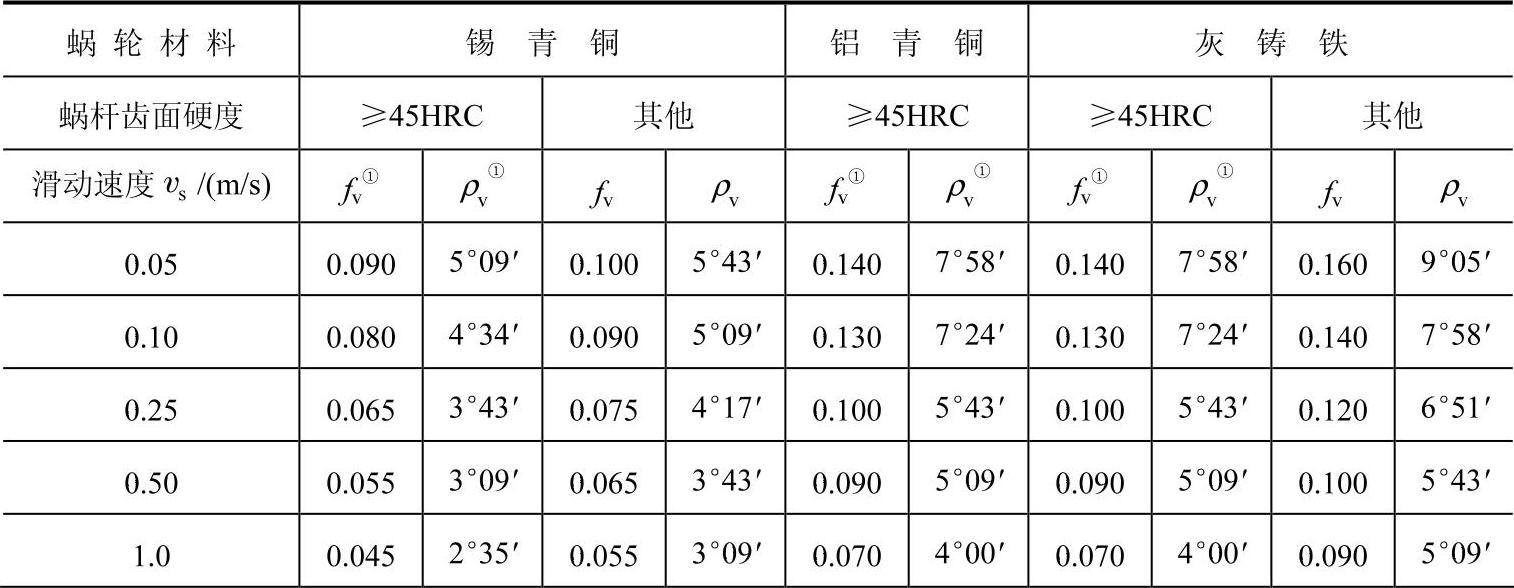
（续）

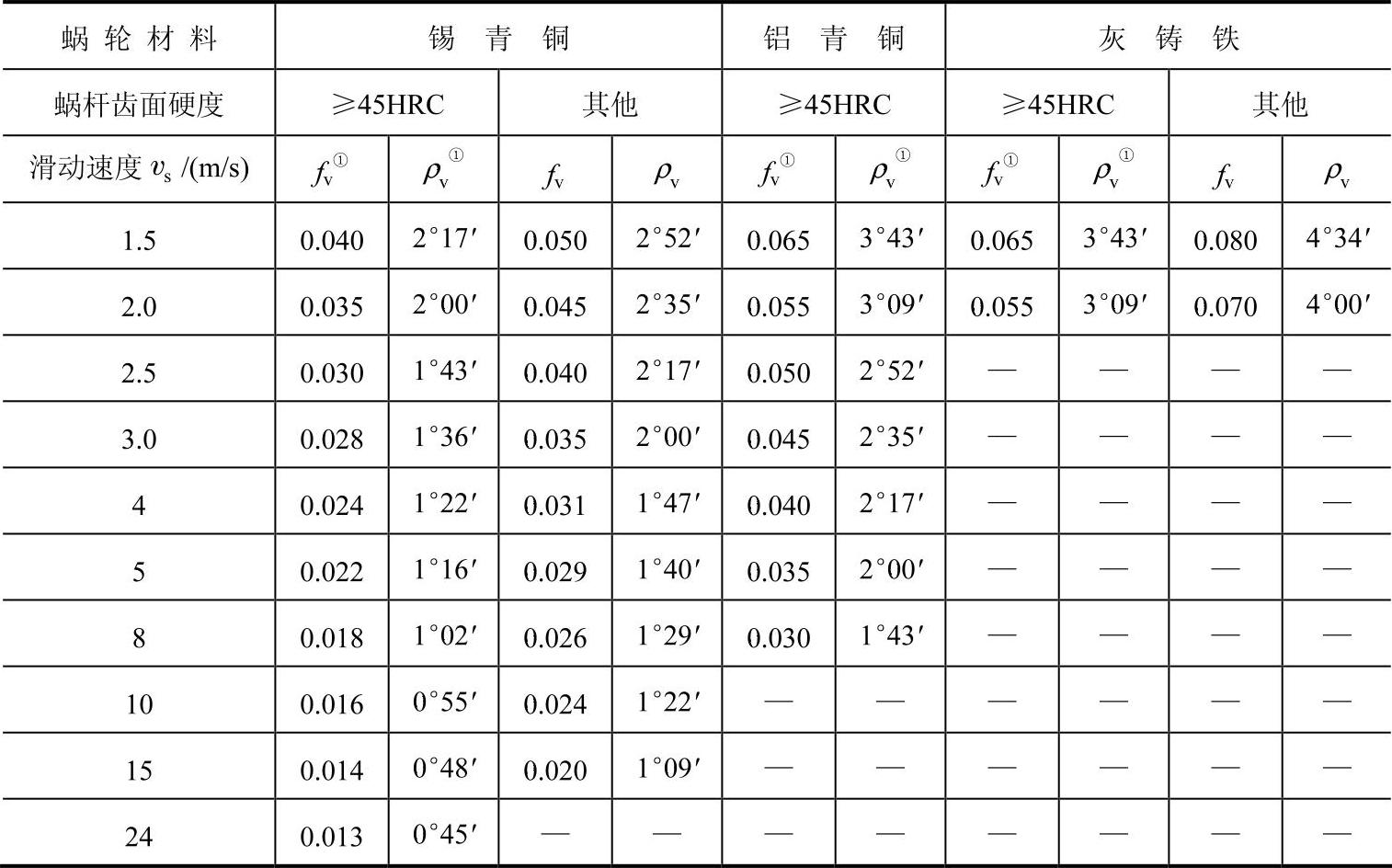
①列内数值对应蜗杆齿面粗糙度轮廓算术平均偏差Ra为1.6～0.4μm，经过仔细跑合，正确安装，并采用黏度合适的润滑油进行充分润滑的情况。

（2）几何尺寸

1）几何尺寸计算。普通圆柱蜗杆传动的几何尺寸如图6-49所示，其主要几何尺寸计算公式见表6-60及表6-61。

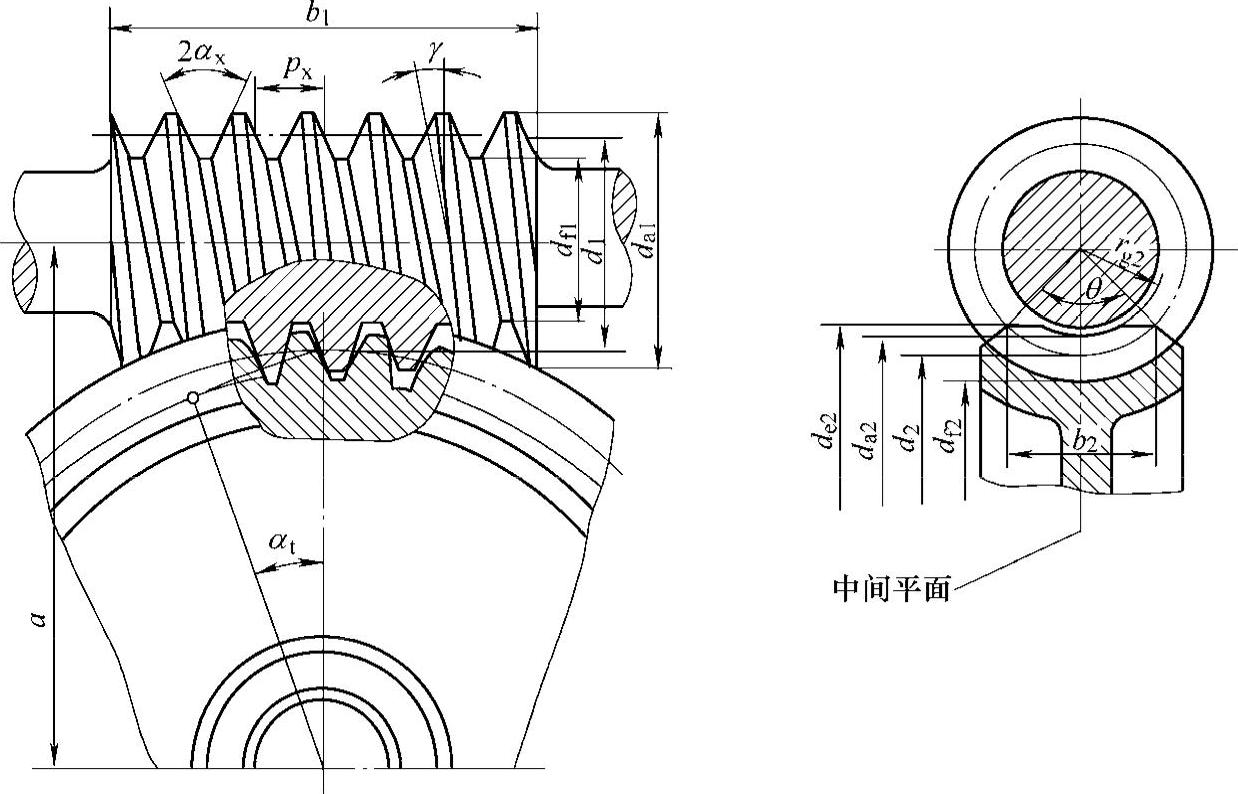
图6-49 普通圆柱蜗杆传动的几何尺寸

表6-60 普通圆柱蜗杆传动的主要几何尺寸计算公式

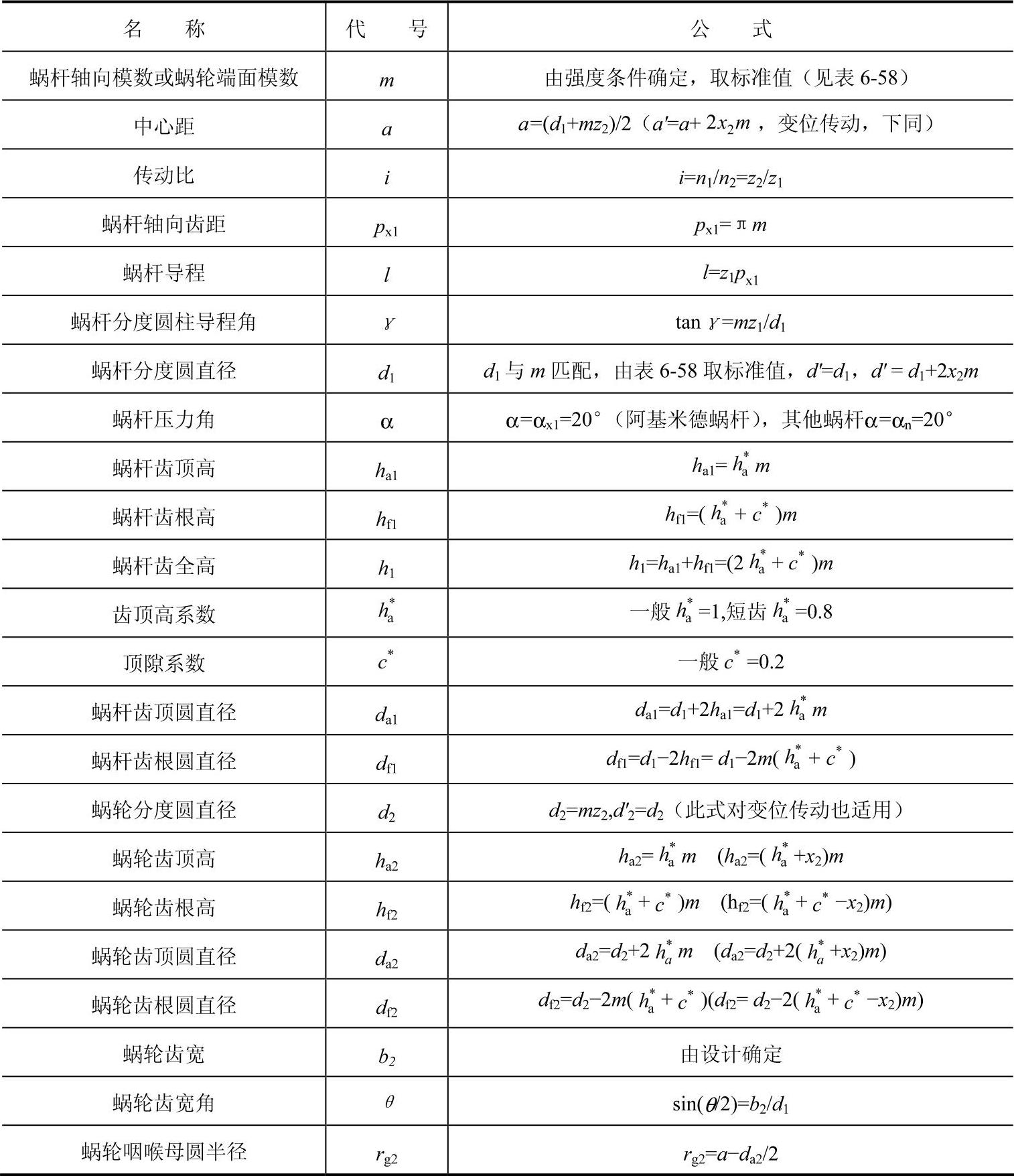
表6-61 蜗杆螺纹部分长度b₁、蜗轮外径d_e2及蜗轮宽度B的计算公式

（续）

2）蜗杆传动的变位特点。变位蜗杆传动主要用于配凑中心距或改变传动比，使之符合推荐值，强度方面的考虑是次要的。蜗杆传动的变位方法与齿轮传动的变位方法相似，即不改变刀具尺寸，利用刀具相对蜗轮毛坯的径向位移来实现变位。但是在蜗杆传动中，由于蜗杆的齿廓形状和尺寸要与加工蜗轮的滚刀形状和尺寸相同，所以为了保持刀具尺寸不变，蜗杆尺寸是不能变动的，因而只能对蜗轮进行变位。其变位特点是蜗杆变位前后顶圆、根圆、分度圆、齿厚的尺寸不变，变位后分度圆与节圆不重合；蜗轮变位前后节圆与分度圆始终重合，其他尺寸有变化。图6-50表示了几种变位情况，a′、z₂′分别为变位后的中心距和蜗轮齿数，x₂为蜗轮变位系数。

图6-50b为标准蜗杆传动，变位蜗杆传动根据使用场合的不同，可在下述两种变位方法中选取一种。

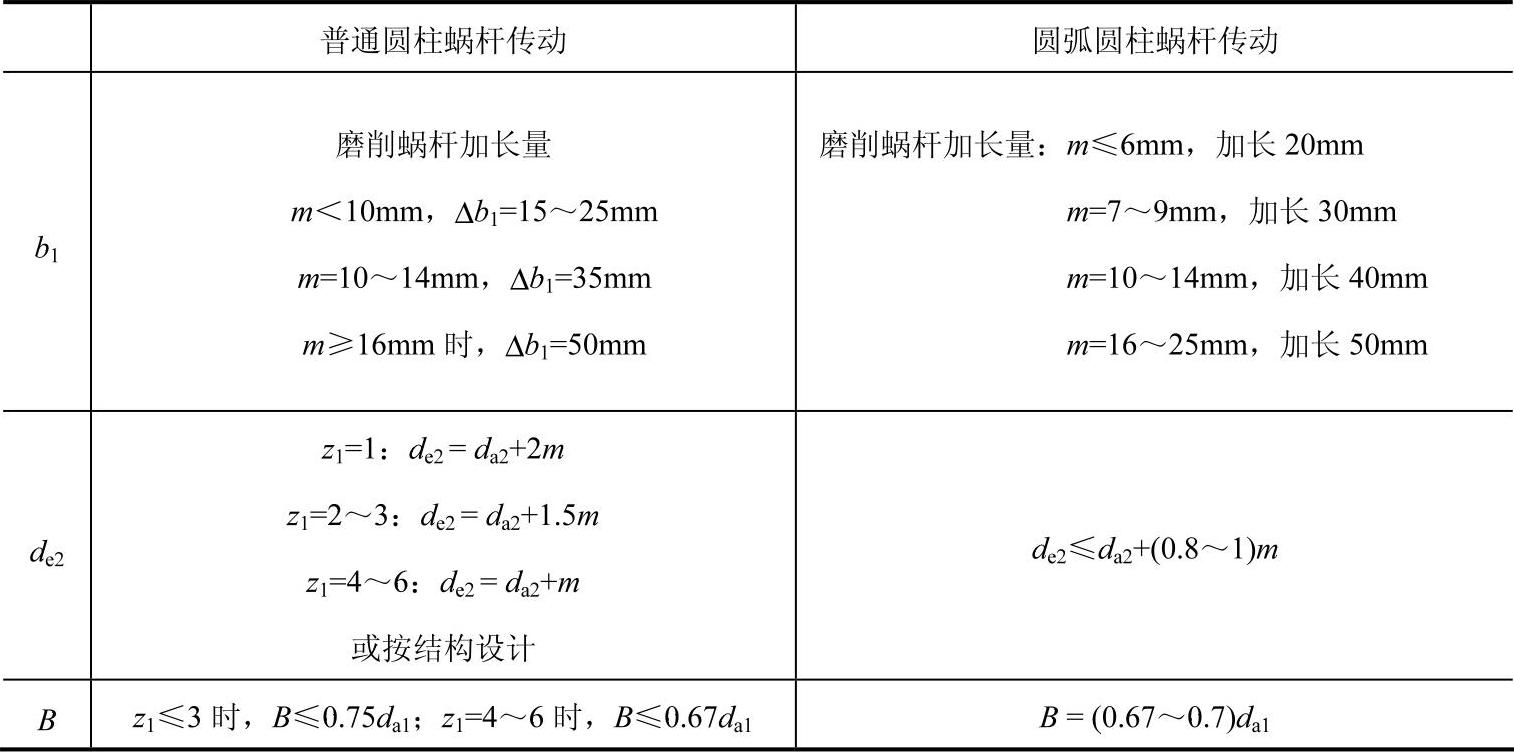
①调整中心距而不改变传动比的变位。这种变位前后蜗轮齿数保持不变，即z₂′=z₂，而传动的中心距发生变化，即a′≠a，如图6-50a、c所示，变位后蜗杆与蜗轮的节圆直径分别为

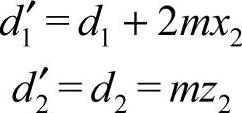
变位后的中心距a′为

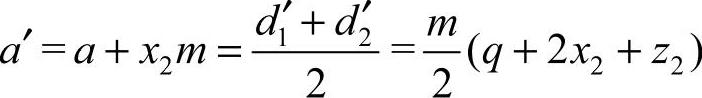
据此可求出变位系数x₂为

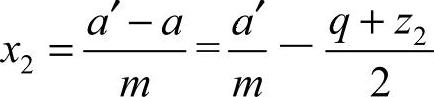
由此可见，当x₂＞0时，中心距变大，由于蜗轮齿数不变，故其轮齿变厚，强度增大；当x₂＜0时，中心距变小，其轮齿变薄，强度降低。为了有利于蜗轮轮齿强度的提高，最好采用x₂为正值。蜗轮变位系数常用范围为-0.5≤x₂≤+0.5。

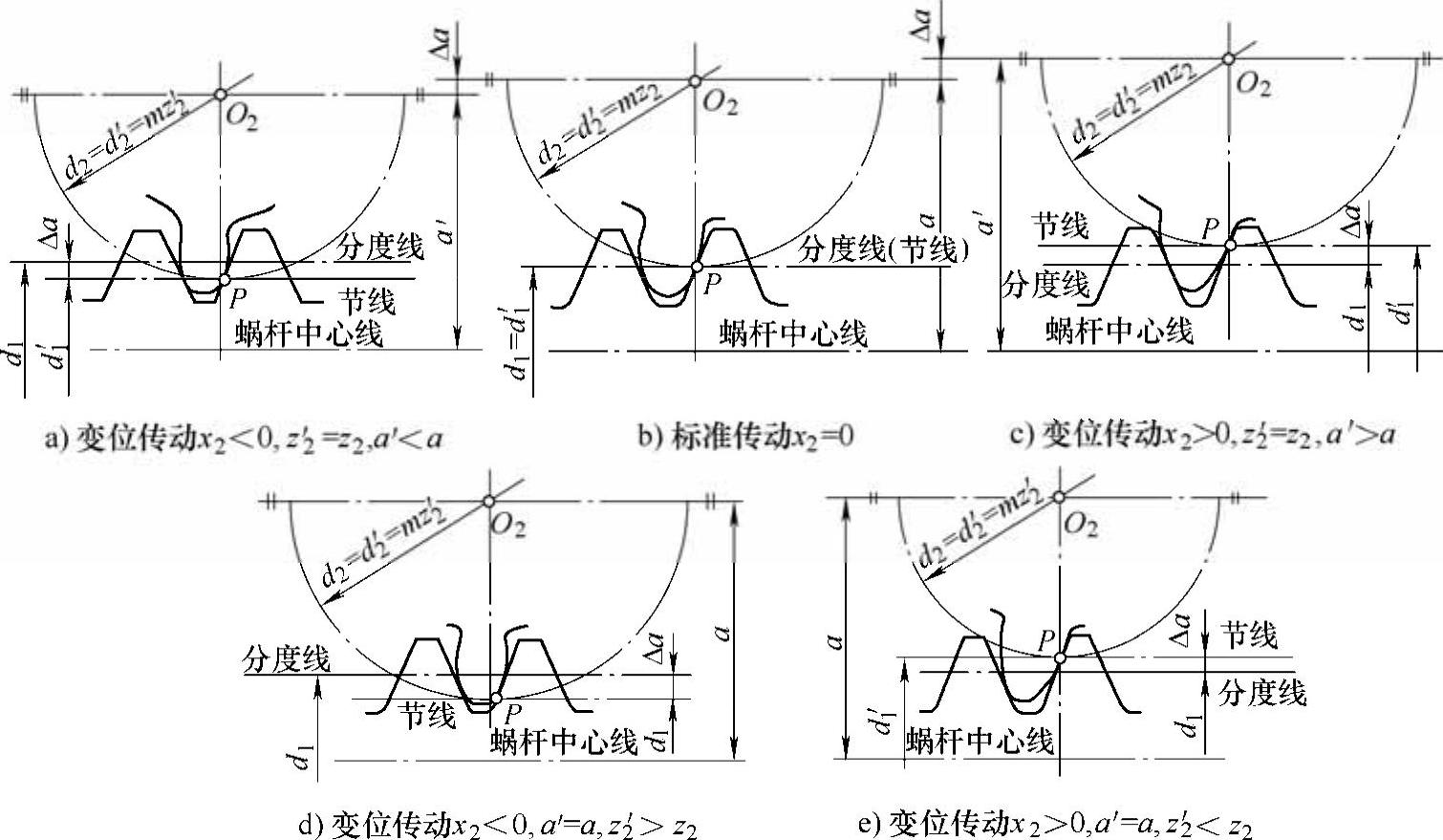
图6-50 蜗杆传动的变位

②调整传动比而不改变中心距的变位。这种变位前后传动的中心距保持不变，即a′=a，而蜗轮齿数发生变化，即z₂′≠z₂，通常将蜗轮齿数增加或减小一二个齿，如图6-50d、e所示。此时，传动的啮合节点发生了改变，中心距可表示为

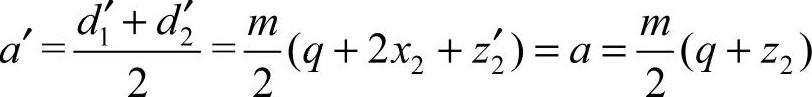
故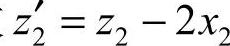，则。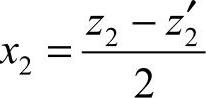

由此可见，当x₂＞0时，齿数变少，轮齿变厚，强度增大；当x₂＜0时，齿数变多，轮齿变薄，强度降低。若z₂-z₂′=±1，则x₂=±0.5；若z₂-z₂′=±2，则x₂=±1。

3.失效形式及设计准则

蜗杆传动的失效形式与齿轮传动相同，有点蚀、胶合、磨损、轮齿折断等。与平行轴圆柱齿轮相比，蜗杆和蜗轮齿面间还有沿蜗轮齿方向的滑动，而且相对滑动速度大，效率低，发热量大，因而蜗杆传动更容易发生胶合和磨损失效。由于蜗杆的齿是连续的螺旋齿，且其材料的强度比蜗轮高，所以失效一般发生在蜗轮齿上。

在闭式传动中，蜗杆传动多因胶合或点蚀失效，设计准则为按蜗轮齿面的接触疲劳强度进行设计，对齿根弯曲疲劳强度进行校核。另外，闭式蜗杆传动的散热不良时会降低蜗杆传动的承载能力，加速失效，故应作热平衡计算。当蜗杆轴细长且支承跨距大时，还应进行蜗杆轴的刚度计算。

对开式传动，蜗轮多发生齿面磨损和轮齿折断，所以应将保证蜗轮齿根的弯曲疲劳强度作为开式蜗杆传动的设计准则。

4.蜗轮和蜗杆的材料和结构

（1）蜗杆传动的材料 蜗轮和蜗杆的材料不仅要求有足够的强度，更重要的是配对的材料应具有较好的减摩、耐磨、抗胶合、易跑合的特性。

1）蜗杆材料。实验证明，在蜗杆齿面粗糙度满足技术要求的前提下，蜗杆、蜗轮齿面硬度差越大，抗胶合能力越强，通常蜗杆的齿面硬度应高于蜗轮，故用热处理的方法提高蜗杆齿面硬度很重要，这就要求蜗杆材料要具有良好的热处理、切削和磨削性能。

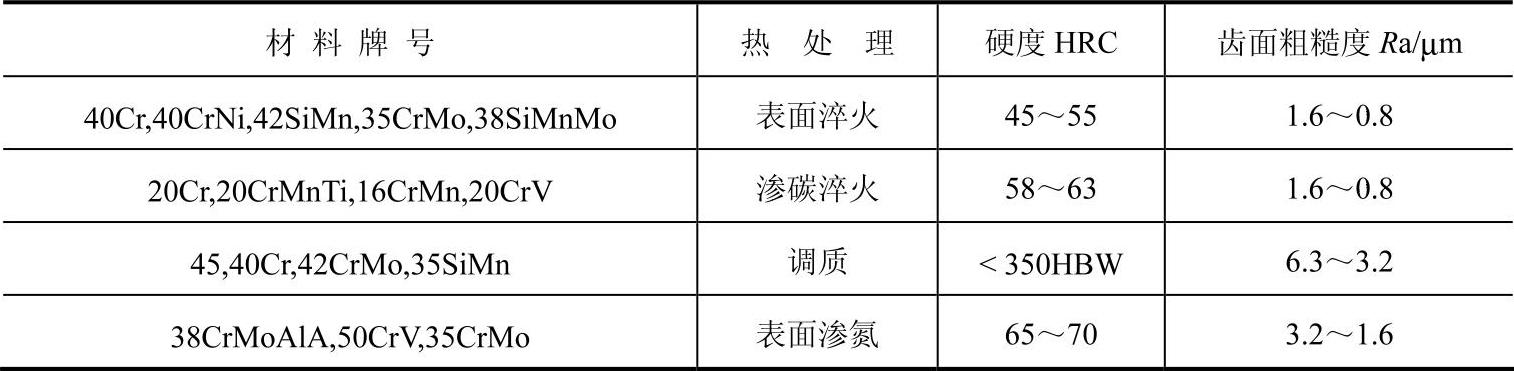
常用的蜗杆材料有碳钢和合金钢两类。按热处理的不同可分为硬面蜗杆和调质蜗杆，设计时应首先考虑选用硬齿面蜗杆，但要注意硬齿面蜗杆制造时必须磨削。在缺乏磨削设备或蜗杆传动承受短期冲击载荷作用时，可选用调质蜗杆。常用蜗杆材料及工艺要求见表6-62。

表6-62 常用蜗杆材料及工艺要求

2）蜗轮材料。蜗轮材料通常是指蜗轮齿冠部分的材料。考虑到蜗杆传动难于得到高的接触精度，又加滑动速度又较大，以及蜗杆变形等因素，故蜗杆、蜗轮不能都用硬材料制造，通常蜗轮用减摩性良好的软材料来制造。设计时可根据滑动速度v_s选择蜗轮材料，常用的材料如下。

①铸造锡青铜。其耐磨性最好，抗胶合能力高，易加工，用于重要传动，允许的滑动速度v_s可达25m/s，但价格较贵。常用的有ZCuSn10Pb1、ZCuSnPb5Zn5。其中后者常用于v_s＜12m/s的传动。

②铸造铝青铜。强度较高但价格较锡青铜便宜，其他性能均比锡青铜略差，一般用于v_s＜4m/s的传动且与之配套的蜗杆硬度不低于45HRC。常用的有ZCuAl10Fe3、ZCuAl10Fe3Mn2等。

③灰铸铁。其各项性能远不如前面两类材料，但价格便宜。适用于v_s＜2m/s的低速且对效率要求不高的一般传动。

为了防止变形，常对蜗轮进行时效处理。

（2）蜗杆和蜗轮的结构

1）蜗杆的结构。蜗杆螺旋部分的直径一般与轴径相差不大，因此蜗杆多与轴做成一体，称为蜗杆轴，结构如图6-51。常用车或铣加工，车制如图6-51a所示，仅适用于蜗杆齿根圆直径d_f1大于轴径d₀时；铣制如图6-51b所示，无退刀槽，且d_f1可小于d₀，所以其刚度较车制蜗杆大。当蜗杆根圆与相配的轴的直径之比d_f1/d₀＞1.7时，可采用装配式。

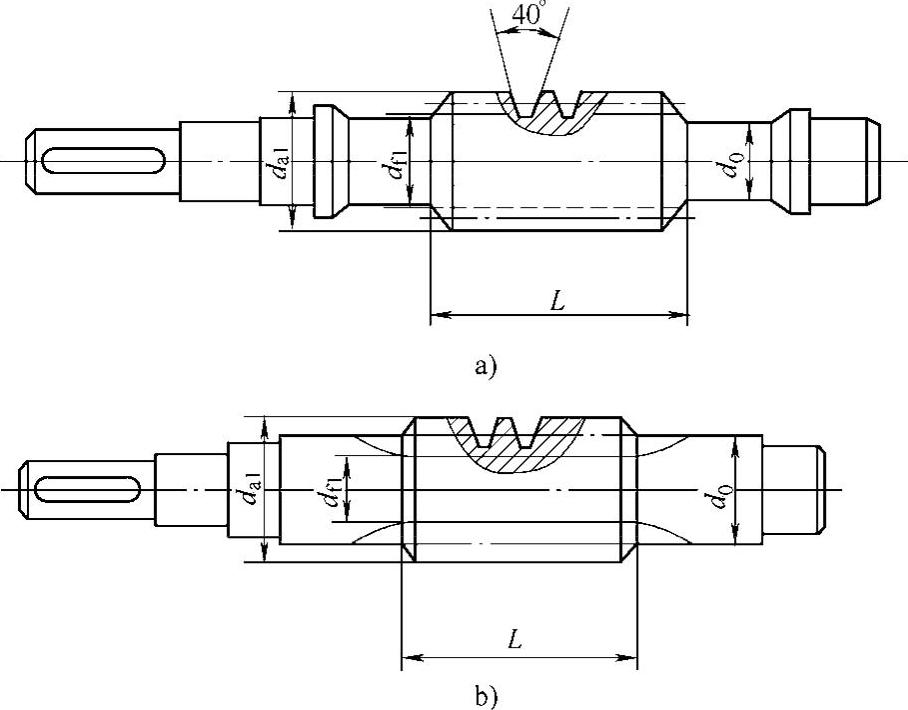
图6-51 蜗杆的结构

2）蜗轮的结构。蜗轮的结构可分为整体式和组合式，如图6-52所示。整体式适用于铸铁蜗轮、铝合金蜗轮及分度圆直径小于100mm的青铜蜗轮，如图6-52a所示。在其他情况下，为了节省贵重金属，一般采用组合式结构。组合式蜗轮可分为三种结构。(www.daowen.com)

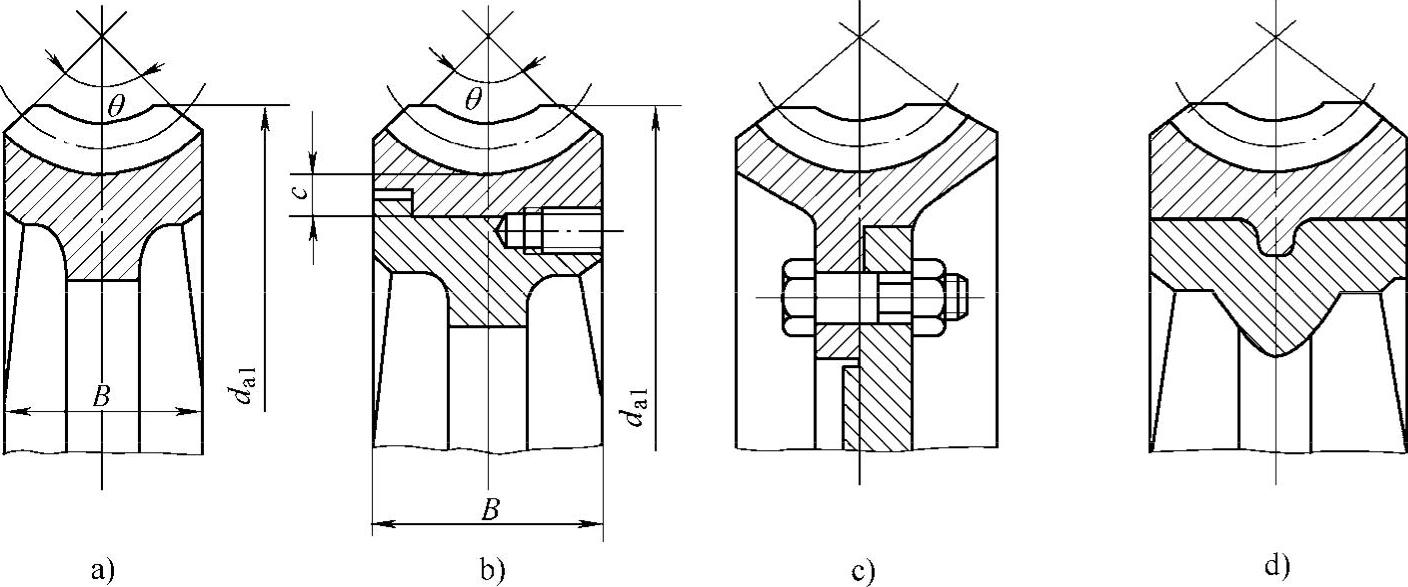
图6-52 蜗轮的结构

①齿圈压配式。为了节约贵重的有色金属，采用青铜蜗轮时，尽可能做成齿圈压配式结构，如图6-52b所示。齿圈与铸铁轮心多用H7/r6过盈配合。为了增加过盈配台的可靠性，有时沿着接合缝还要拧上4～5个螺钉，螺钉孔中心线偏向轮芯轮毂1～2mm，螺钉的直径取（1.2～1.4）倍的模数m，长度取0.3～0.4倍的齿宽b。该结构适用于中等尺寸及工作温度变化较小的蜗轮。

②螺栓联接式。当蜗轮直径较大时，可采用普通螺栓或铰制孔用螺栓联接齿圈和轮心，如图6-52c所示。后者更好，适用于大尺寸蜗轮。

③拼铸式。将青铜齿圈浇注在铸铁轮心上，然后再切齿，如图6-52d所示。该结构适用于批量生产、中等尺寸的蜗轮。

5.蜗杆传动的受力分析

受力分析的目的在于蜗杆传动的强度计算及为轴、轴承的设计计算作准备。蜗杆传动的受力分析和斜齿圆柱齿轮传动类似，与齿轮不同之处在于失效发生在蜗轮上，因此通常受力分析从蜗轮入手，本书受力分析从蜗杆入手，由于蜗杆传动的啮合摩擦功耗大，通常以传动效率η近似考虑该损耗。

（1）力的大小 图6-53所示是以右旋蜗杆为主动件，并沿图示的方向旋转时，蜗杆、蜗轮齿面上的受力情况。设法向力F_n集中作用在节点P处，F_n可分解为圆周力、轴向力和径向力3个正交力，蜗杆上分别为F_t1、F_a1、F_r1；蜗轮上分别为F_t2、F_a2、F_r2。当蜗杆轴与蜗轮轴的轴交角为90°时，由力的作用与反作用原理可知，F_t1与F_a2、F_a1与F_t2、F_r1与F_r2分别为大小相等、方向相反的力。各力大小可按下列各式计算，单位均为N。

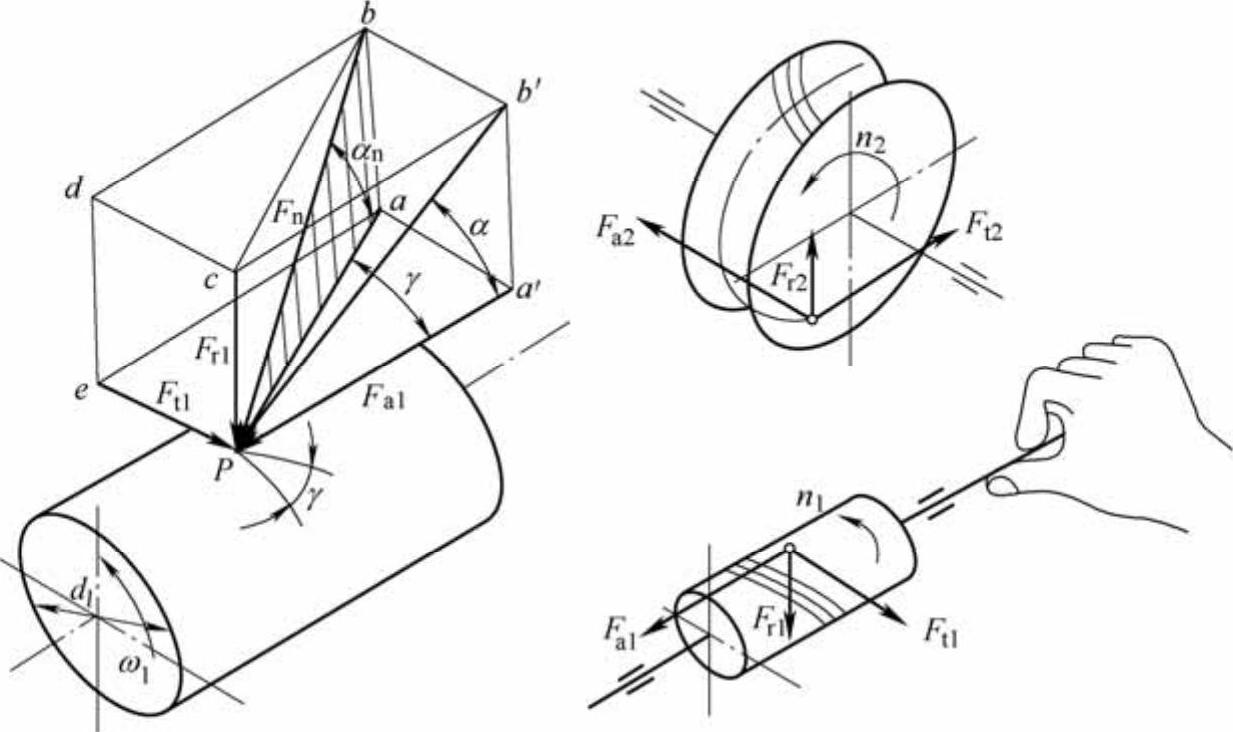
图6-53 蜗杆传动的受力分析

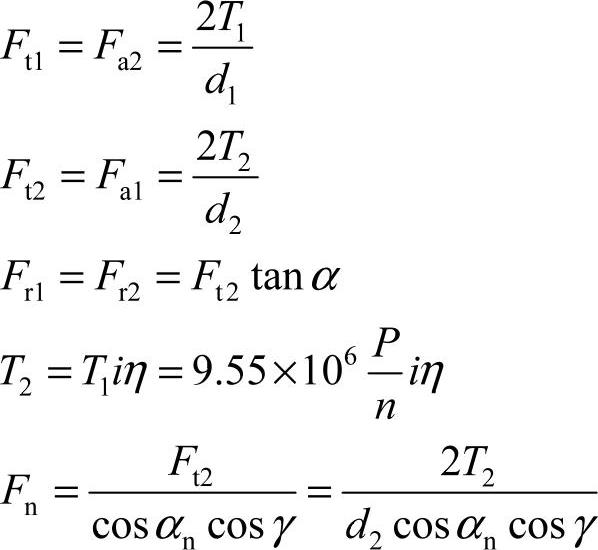
式中 T₁，T₂——蜗杆、蜗轮的转矩（N·mm）。

（2）力的方向 蜗杆上圆周力、径向力和蜗轮上径向力方向的判别，方法与直齿圆柱齿轮传动相同。蜗杆上的轴向力的方向取决于其螺旋线的旋向和蜗杆的转动方向，可按“主动轮右（左）手法则”确定，右旋用右手，左旋用左手；蜗轮上圆周力、轴向力的方向分别与蜗杆上轴向力、圆周力方向相反。蜗轮的转动方向与F_t2的方向一致。

6.蜗杆传动的强度计算

闭式蜗杆传动的强度主要取决于蜗轮轮齿的齿面接触疲劳强度和齿根弯曲疲劳强度；开式传动仅取决于蜗轮轮齿的齿根弯曲疲劳强度。

（1）蜗轮齿面接触疲劳强度计算 由蜗杆传动实质可知，在中间平面内，蜗杆传动类似于斜齿轮与斜齿条的传动，故可依据赫兹接触应力公式仿照斜齿轮的分析方法计算蜗轮齿面的接触应力，并对其进行限制，以防止点蚀的发生。

由于阿基米德（ZA）蜗杆具有直线齿廓，ρ₁趋近无穷大，故节点处的综合曲率半径为

ρ∑=ρ₁ρ₂/（ρ₁+ρ₂）≈ρ₂=d₂sinα/（2cosγ）

将ρ∑和其他相应参数代入Hertz公式，整理后可得蜗轮齿面接触疲劳强度的验算公式为

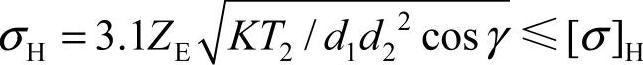
将d₂=mz₂代入上式得出蜗轮齿面接触疲劳强度的设计公式为

m²d₁≥9.6KT₂cosγ[Z_E/（z₂[σ]_H）]²

式中 K——载荷系数，K=K_AK_βK_v，其中K_A为使用系数，查表6-63；

K_β——齿向载荷分布系数，当蜗杆传动在平稳载荷下工作时，载荷分布不均现象将由于工作表面良好的磨合而得到改善，此时，可取K_β=1；当载荷变化较大，或有冲击、振动时，可取K_β=1.3～1.6；

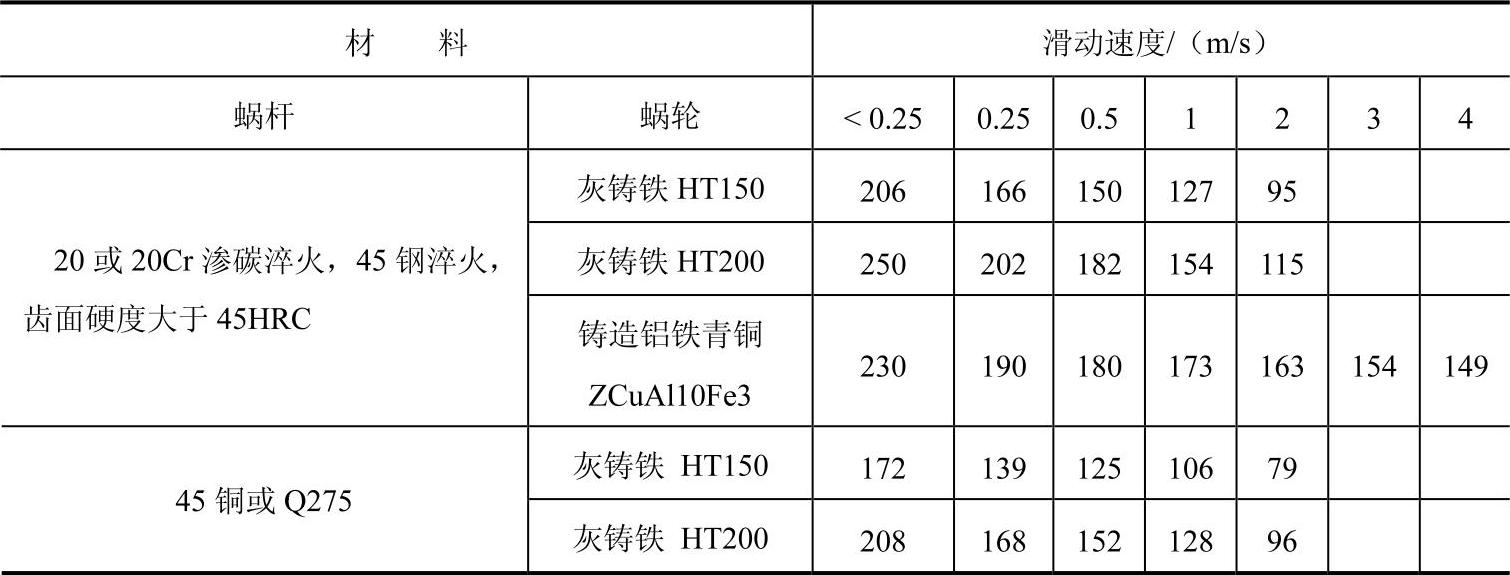
K_v——动载系数，由于蜗杆传动一般较平稳，动载荷要比齿轮传动的小得多，故对于精密制造，且蜗轮圆周速度v₂≤3m/s时，取K_v=1.0～1.1；v₂＞3m/s时，取K_v=1.1～1.2；

Z_E——材料系数，查表6-64；

cosγ——查表6-65；

[σ]_H——蜗轮材料的许用接触应力，单位为MPa。其值取决于蜗轮材料的强度和性能。当材料为锡青铜（σ_b＜300MPa），蜗轮主要为接触疲劳失效，其许用应力[σ]_H与应力循环次数N有关，[σ]_H=Z_N[σ]_0H，其中[σ]_0H为基本许用接触应力，见表6-66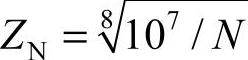；称为寿命系数，N的计算方法与齿轮的计算方法相同，但是当N＞25×10⁷时，取N=25×10⁷；当N＜2.6×10⁵时，取N=2.6×10⁵。当蜗轮材料为铝青铜或铸铁（σ_b≥300MPa），蜗轮主要为胶合失效，其许用应力[σ]_H与滑动系数有关而与应力循环次数N无关，其值可直接由表6-67查取。

计算出蜗杆传动中心距a后，可根据预定的传动比i从表6-58中选择一合适的a值，以及相应的蜗杆、蜗轮的参数。

表6-63 使用系数K_A

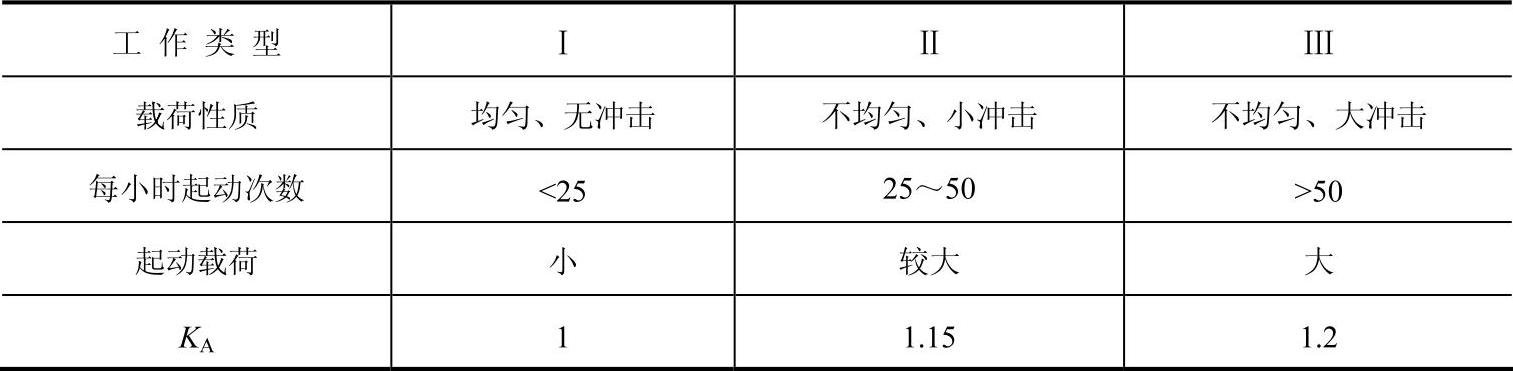
表6-64 材料系数Z_E （单位：MPa）

表6-65 cosγ值

表6-66 锡青铜蜗轮的基本许用接触应力[σ]_0H （单位：MPa）

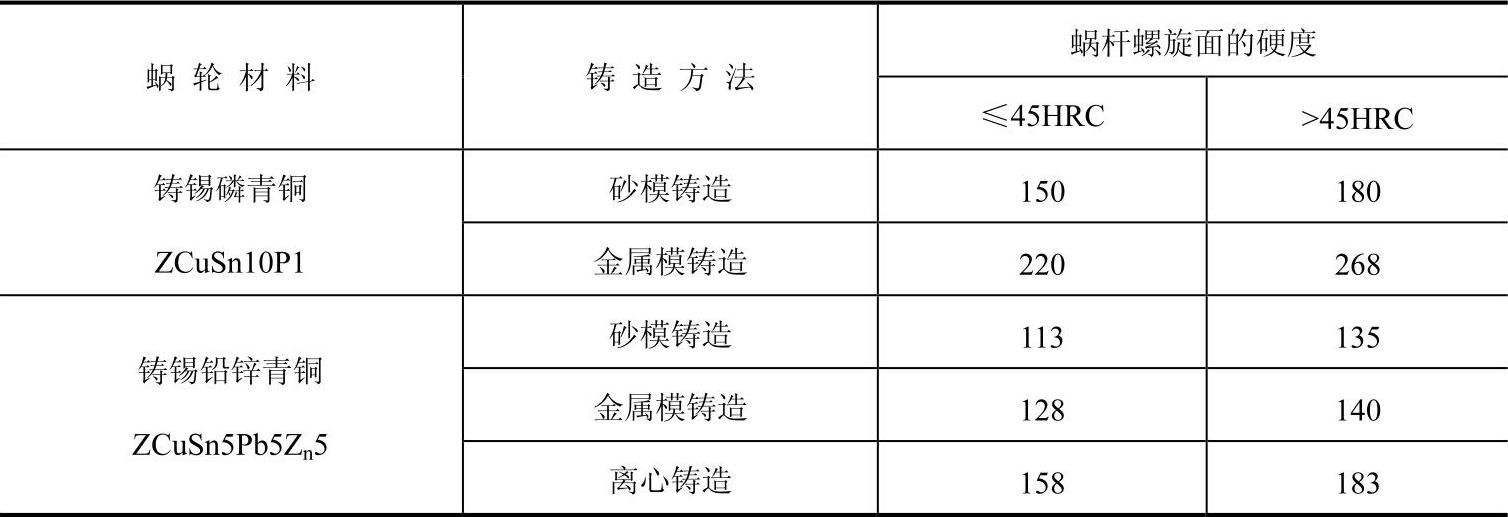
表6-67 铝青铜及铸铁蜗轮的许用接触应力[σ]_H （单位：MPa）

（2）蜗轮齿根弯曲疲劳强度计算 当蜗轮齿数z₂＞90或开式传动中，蜗轮轮齿常因弯曲强度不足而失效。在闭式蜗杆传动中通常只作弯曲强度的校核计算，但这种计算是必须进行的。因为蜗轮轮齿的弯曲强度不只是为了判别其弯曲断裂的可能性，对于承受重载的动力蜗杆副，蜗轮轮齿的弯曲变形量直接影响到蜗杆副的运动平稳性精度。

由于蜗轮的形状较复杂，且离中间平面越远的平行截面上轮齿越厚，故其齿根弯曲强度高于斜齿轮。因此，蜗轮轮齿的弯曲疲劳强度难于精确计算，只能进行条件性的概略估算。按照斜齿圆柱齿轮的计算方法，经推导可得蜗轮齿根弯曲疲劳强度的验算公式为

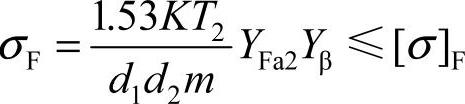
将d₂=mz₂带入上式并整理，得设计式

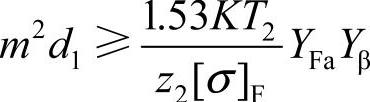
式中 [σ]_F——蜗轮的许用弯曲应力（MPa），其值[σ]_F=[σ]_0FY_N，其中[σ]_0F为考虑齿根应力修正系数后的基本许用弯曲应力，见表6-68；Y_N为寿命系数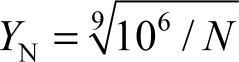，；N为应力循环次数，计算方法同前，

当N＞25×10⁷时，取N=25×10⁷；当N＜10⁵时，取N=10⁵；

Y_Fa2——齿形系数，按蜗轮当量齿数z_v2=z/cos³γ及蜗轮的变位系数查图6-54；

Y_β——螺旋角系数，Y_β=1-γ/140°。

表6-68 铝青铜及铸铁蜗轮的许用接触应力[σ]_0F （单位：MPa）

7.蜗杆轴的刚度计算

如果蜗杆刚度不足，受载后产生过大的变形，就会影响正确啮合，造成偏载，加剧磨损。因此，对于受力后会产生较大变形的蜗杆，必须进行蜗杆弯曲刚度的校核计算。校核时通常将蜗杆螺旋部分看成以蜗杆齿根圆直径为直径的轴段，采用条件性计算，其刚度条件为

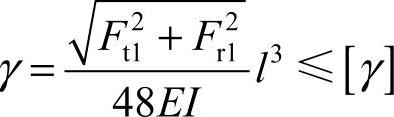
式中 γ——蜗杆弯曲变形的最大挠度（mm）；

I——蜗杆危险截面的惯性矩（mm⁴），I=πd_f⁴1/64，其中d_f1为蜗杆齿根圆直径；

E——蜗杆材料的拉、压弹性模量，通常E=2.06×10⁵MPa；

l——蜗杆两端支承间的跨距（mm），视具体结构而定，初步计算时可取l≈0.9d₂，d₂为蜗轮分度圆直径；

[γ]——蜗杆许用最大挠度（mm），通常取[γ]=d₁/1000，此处d₁为蜗杆分度圆直径。

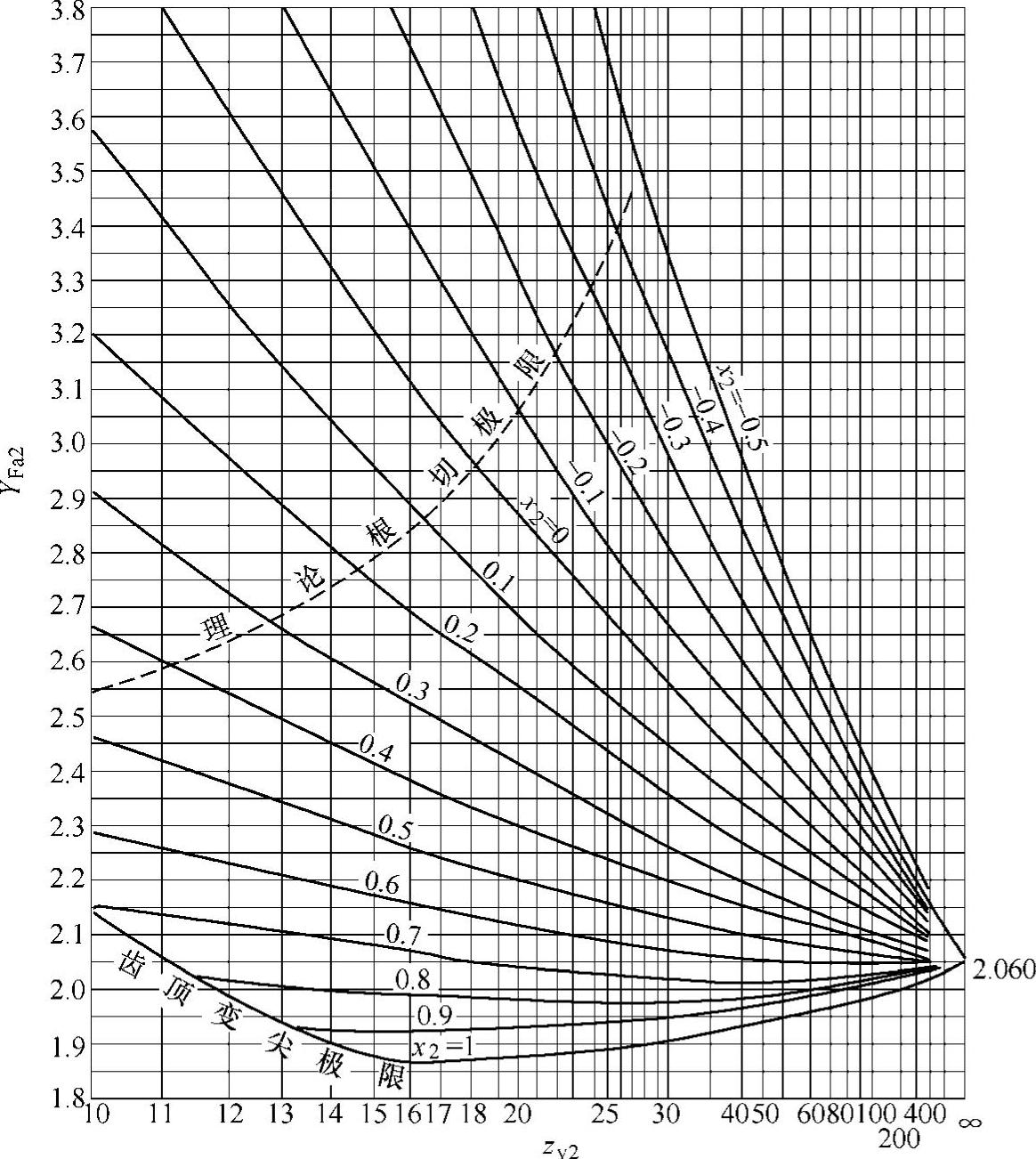
图6-54 蜗轮齿形系数

8.蜗杆传动的热平衡计算

蜗杆传动由于齿面相对滑动速度大，工作时摩擦发热严重，尤其在闭式传动中，如果箱体散热不良，润滑油的温度过高将降低润滑的效果，从而增大摩擦损失，甚至发生胶合。为了使油温保持在允许范围内，防止胶合的发生，必须进行热平衡的计算。

在热平衡状态下，蜗杆传动单位时间内由摩擦功耗产生的热量等于箱体散发的热量，即

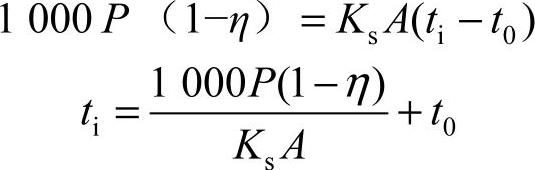
式中 P——蜗杆传递的功率（kW）；

K_s——箱体表面传热系数，即单位箱体面积、单位温差吸收或放出热量，可取K_s=（8.15～17.45）W/（m²·℃），当周围空气流通良好时，取偏大值；

t₀——周围空气的温度，通常取t₀=20℃；

t_i——热平衡时油的工作温度，一般限制在60～70℃，最高不超过80℃；

A——箱体有效散热面积（m²），即箱体内表面能被润滑油浸到或飞溅到、而外表面直接与空气接触的箱体表面积。如果箱体有散热片，则有效面积按原面积的1.5倍估算；对于散热片布置良好的固定式蜗杆减速器，其散热面积可按A=9×10^-5a^1.88估算，其中a为中心距。

当油温超过80℃时，说明散热面积不足，可用以下散热措施提高散热能力。

1）加散热片，增加散热面积。采用散热片时，为保持正常工作的油温所需的总散热面积为

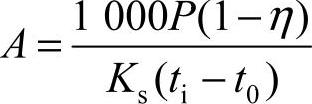
2）在蜗杆轴端加装风扇，提高表面传热系数。如图6-55a所示，加装风扇时表面传热系数K_s′可按表6-69选取。此时，总功耗加大，传动总效率η除了考虑啮合效率η₁、轴承效率η₂、搅油效率η₃外，还应考虑风扇效率η₄。

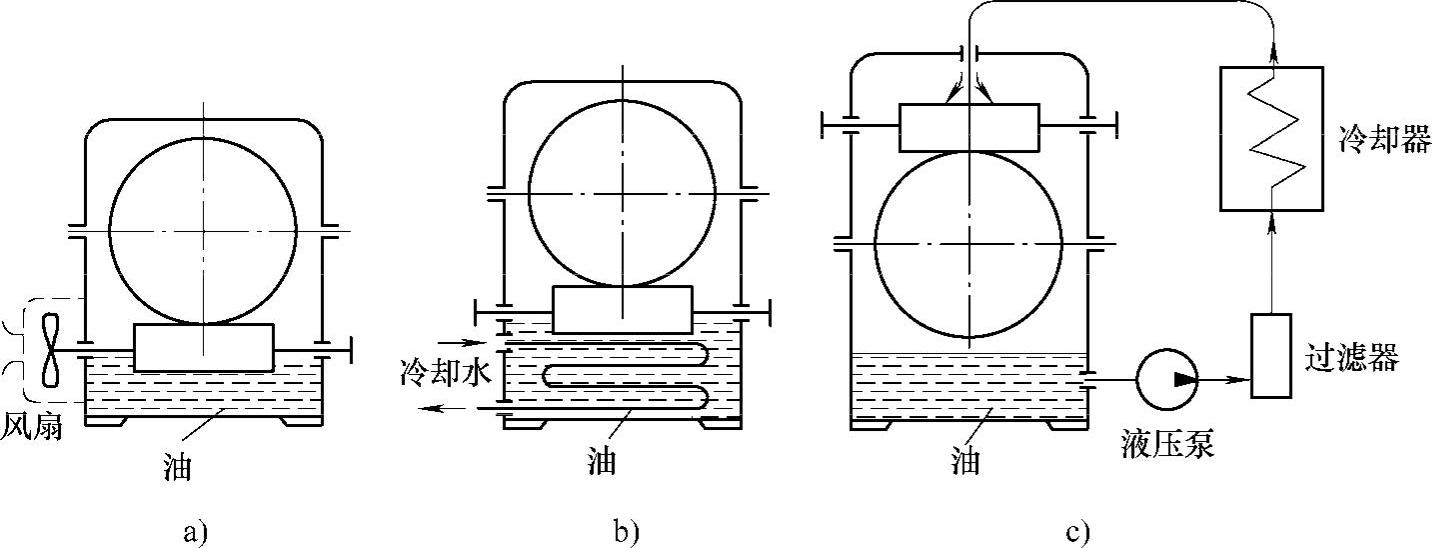
图6-55 蜗杆传动的散热方法

风扇功耗ΔP_F为

ΔP_F=1.5v_F³×10^-5

v_F=πD_Fn_F/（60×1000）

式中 ΔP_F——风扇功耗（kW）；

v_F——风扇叶轮的圆周速度（m/s）；

D_F——风扇叶轮外径（mm）；

n_F——风扇转速（r/min）。

风扇效率为

η₄=（P-ΔP_F）/P

表6-69 风冷时的表面传热系数

此时蜗杆传动的总效率为η=η₁η₂η₃η₄，因此由摩擦功耗所产生的热量H₁（W）为

H₁=1000P（1-η）

散发到空气中的热量H₂（W）为

H₂=（K_s′A₁+K_sA₂）（t_i-t₀）

式中 A₁，A₂——风冷面积及自然冷却面积（m²）。

其他符号意义同前。

加装风扇后达到热平衡时的工作油温为

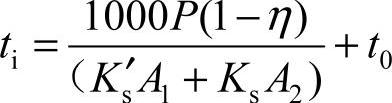
3）加循环冷却设施。如图6-55b所示，在油池中安装循环蛇形冷却水管，使冷水和油池中热油进行热交换，以达降低油温之目的。

4）外冷却喷油润滑。如图6-55c所示，通过外冷却器，将热油冷却后直接喷到蜗杆啮合区，从而降低热平衡时的工作温度。