1.齿轮传动的特点
主要优点:①传动平稳、无噪声;②效率高,达99%以上;③寿命长,一般可达8~10年以上;④因为是啮合传动,因此工作可靠,可用于航天及井下工作的机器;⑤适用的圆周速度和功率范围广,例如超精度齿轮速度可达200m/s;功率可达5×104kW以上;⑥可以实现平行轴、同一平面的相交轴和空间交错轴之间的传动。
缺点:①要求较高的制造和安装精度,成本较高;②不适于远距离两轴间的传动。
2.齿轮传动的失效形式及设计准则
(1)失效形式
1)轮齿折断。因为轮齿受力时齿根弯曲应力最大,而且有应力集中,因此轮齿折断一般发生在齿根部分。
轮齿折断又分为过载折断和疲劳折断,过载折断是由于轮齿因短时严重过载而引起的突然折断,这主要发生于脆性材料。多数齿轮发生疲劳折断,轮齿看作悬臂梁,在载荷的多次重复作用下,弯曲应力超过弯曲疲劳极限时,齿根部分将产生疲劳裂纹,然后逐渐扩展,最终将引起轮齿折断,称为疲劳折断。若轮齿单侧工作,其应力按脉动循环变化。若轮齿双侧工作时,则弯曲应力按对称循环变化。
2)齿面失效
①齿面磨损。当啮合齿面间落入磨料性物质时,轮齿工作表面被逐渐磨损,使齿轮失去原有的渐开线曲面形状,同时轮齿变薄而导致传动失效,这种磨损称磨粒磨损。
②齿面点蚀。齿面材料在变接触应力(脉动循环)作用下,由于疲劳而产生的剥蚀损伤现象称为齿面点蚀,又称疲劳磨损。齿面上最初出现的点蚀仅为针尖大小的麻点,后逐渐扩散,甚至数点连成一片,最后形成了明显的齿面损伤,使轮齿丧失原有的渐开线曲面形状,产生冲击和噪声。齿面点蚀是闭式软齿传动的主要失效形式,在开式齿轮传动中,由于齿面磨损较快,点蚀还来不及出现或扩展即被磨掉,所以看不到点蚀出现。
③齿面胶合。在高速重载传动中,常因啮合区温度升高而引起润滑失效,致使两齿面金属直接接触并发生粘着。当两齿面相对运动时,较软的齿面沿滑动方向被撕下而形成沟纹,这种现象称为齿面胶合。在低速重载传动中,由于齿面间的润滑油膜不易形成也可能产生胶合破坏。
④齿面塑性变形。在重载下,较软的齿面上可能沿摩擦力方向产生局部的塑性变形,使齿轮失去正确的齿廓,使瞬时传动比发生变化,造成附加的动载荷。这种损坏常出现在过载严重和起动频繁的传动中。
(2)设计准则 设计一般使用的齿轮传动时,通常只按保证齿根弯曲疲劳强度及保证齿面接触疲劳强度两个准则进行计算。对于高速、大功率的齿轮传动,还要保证齿面抗胶合能力的准则进行计算。至于抵抗其他失效的能力一般不进行计算,但应采取相应的措施,以增强齿轮抵抗这些失效的能力。主要设计准则如下。
1)闭式齿轮传动的设计准则
①中、轻载荷闭式软齿面齿轮传动,因其主要失效形式为齿面疲劳点蚀,故按接触疲劳强度设计,按弯曲强度校核。
②齿面硬度很大、齿芯强度又较低或材质较脆的齿轮的设计准则。因其主要失效形式为疲劳折断,故按弯曲疲劳强度设计,按接触强度校核。
③齿面硬度相同的闭式硬齿面齿轮的设计准则。因其主要失效形式为点蚀或疲劳折断,故应视具体情况而定。
④大功率闭式齿轮传动的设计准则。当输入功率超过75kW时,由于发热量大、易导致润滑不良及轮齿胶合损伤等,还须作热平衡计算。
2)开式或半开式齿轮传动的设计准则。对于开式(半开式)齿轮传动,应根据保证齿面抗磨损及齿根抗折断能力分别进行计算,但鉴于目前对齿面抗磨损的能力尚无完善的计算方法,因此,仅以保证齿根弯曲疲劳强度作为设计准则。为了延长开式(半开式)齿轮传动的寿命,应适当降低开式传动的许用弯曲应力(如将闭式传动的许用弯曲应力乘以0.7~0.8),以使计算的模数值适当增大;或将计算出的模数增大10%~15%,以考虑磨损对齿厚的影响。
3.材料选择及热处理
为了防止齿轮的各种失效,设计齿轮传动时,应使齿面具有较高的抗磨损、抗点蚀、抗胶合及塑性变形的能力,而齿根要求有较高的抗折断的能力。因此,对齿轮材料性能的基本要求为齿面要硬、齿芯要韧、易于加工和热处理。
常用的齿轮材料是各种牌号的优质碳素钢、合金结构钢等。表6-53列出了常用齿轮材料及其热处理后的硬度。
表6-53 常用齿轮材料及其热处理后的硬度
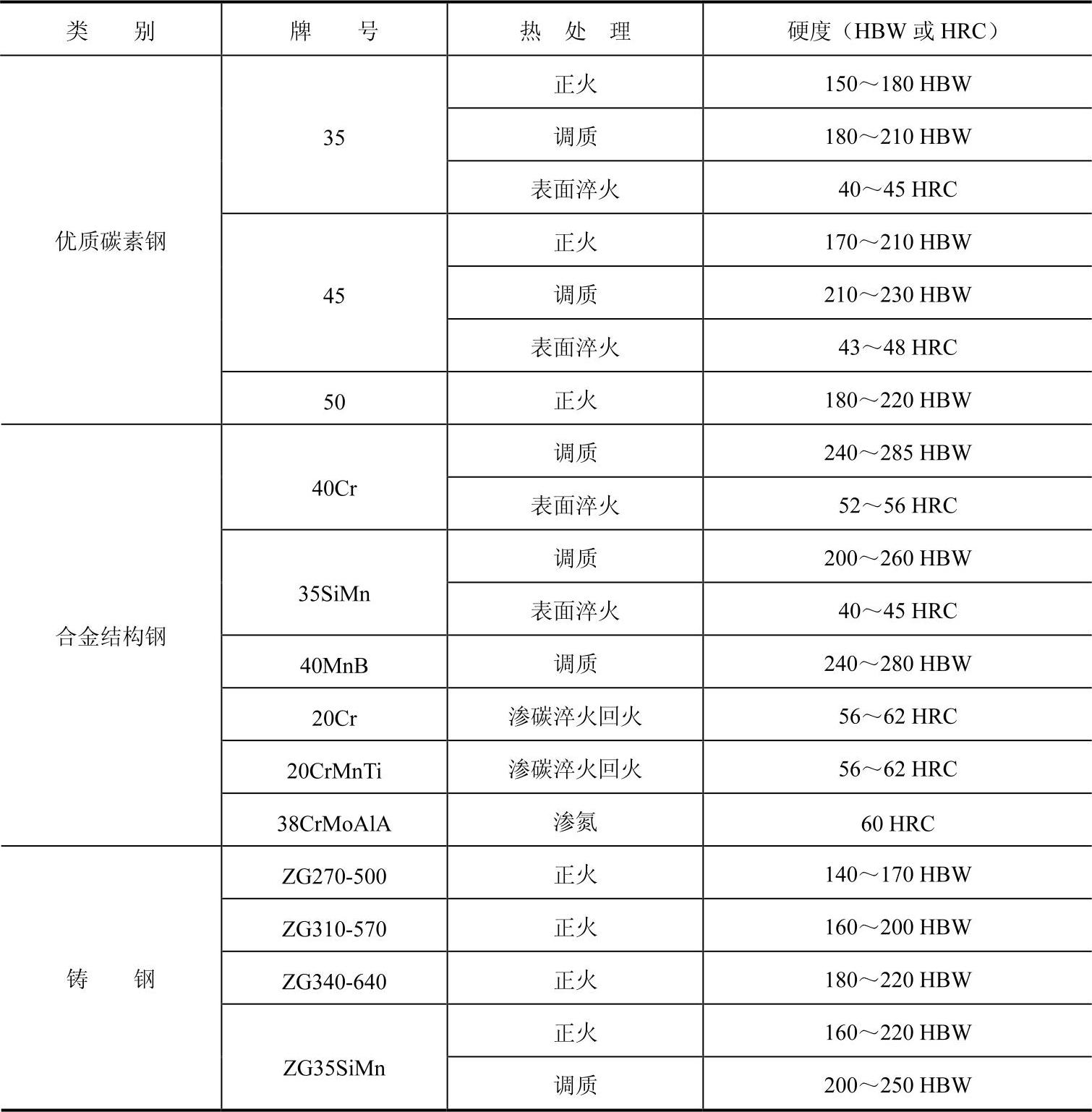
齿轮材料的种类很多,在选择时应考虑的因素也很多,下述几点可供选材时参考:
(1)闭式软齿面齿轮传动常用材料 闭式软齿面齿轮传动常用的材料有35、45、40Cr和35SiMn经调质或正火处理。此类材料的特点是制造方便,多用于对强度、速度和精度要求不高的一般机械传动中。
由于小齿轮轮齿工作次数较多,应使其齿面硬度比大齿轮的高出30~50 HBW。
(2)闭式硬齿面齿轮传动常用的材料 闭式硬齿面齿轮传动常用的材料有20、20Cr、20CrMnTi表面渗碳淬火和45,40Cr表面淬火或整体淬火,一般齿面硬度为45~65HRC。通常两齿轮轮齿采用相同的齿面硬度。此类材料的特点是制造较复杂,精度要求高,多用于高速、重载及精密机械中。
(3)大尺寸齿轮及开式低速齿轮传动常用材料 当齿轮尺寸较大(如直径大于400~600mm)而轮坯不易锻造时,可采用铸钢;开式低速传动可采用灰口铸铁;球墨铸铁有时可代替铸钢。
4.直齿圆柱齿轮传动的受力分析
当齿轮的齿廓在节点P接触时,受力如图6-22所示,可将沿啮合线作用在齿面上的法向力Fn分解为两个相互垂直的分力:切于分度圆的圆周力Ft与指向轮心的径向力Fr。
(1)计算公式
Ft=2T1/d1
Fr=Fttanα
Fn=F/cosα
式中 T1——小齿轮所受的转矩(N⋅mm),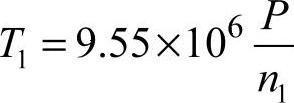 ;
;
P——传递的功率(kW);
n1——小齿轮的转速(r/min);
d1——小齿轮的分度直径(mm);
α——压力角,对标准齿轮α=20o。
(2)力的方向
1)圆周力Ft的方向在主动轮上与运动方向相反,在从动轮上与运动方向相同,且互为作用与反作用力,即Ft1=-Ft2 。
2)径向力Fr的方向分别指向各自的轮心,且互为作用与反作用力,即Fr1=-Fr2 。
5.斜齿圆柱齿轮传动的受力分析
图6-23为斜齿轮齿廓在节点P接触的受力情况,在忽略摩擦力时法向力Fn可分解为圆周力Ft、径向力Fr和轴向力Fa三个分力。
(1)计算公式
Ft=2T1/d1
Fr=Fttanαn/cosβ
Fa=Fttanβ
Fn=Ft/(cosαncosβ)
式中 β——螺旋角;
αn——法面压力角,对标准齿轮αn=20°。
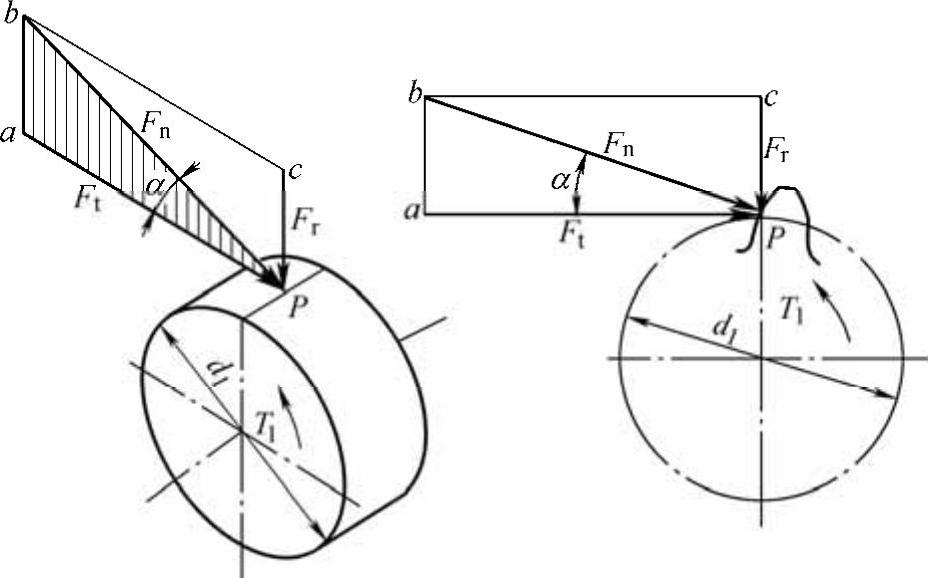
图6-22 直齿圆柱齿轮传动的受力分析
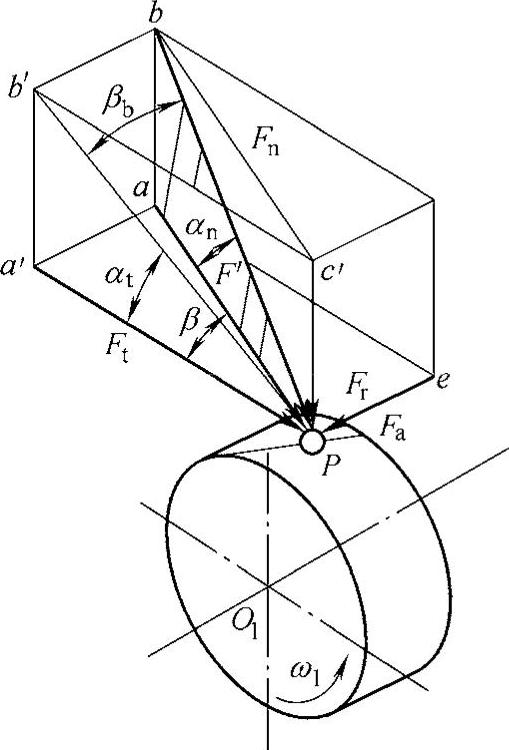
图6-23 斜齿圆柱齿轮传动的受力分析
(2)力的方向
1)圆周力Ft的方向在主动轮上与运动方向相反,在从动轮上与运动方向相同,且互为作用与反作用力,即Ft1=-Ft2 。
2)径向力Fr的方向对两轮都是指向各自的轮心,且互为作用与反作用力,即Fr1=-Fr2 。
3)轴向力Fa的方向需根据螺旋线方向和轮齿工作面而定,也可用主动轮右(左)手螺旋法则判断:当主动轮的螺旋线方向为右(左)旋时也可用右(左)手螺旋定则判断,即伸出右(左)手,四指代表主动轮的转动方向,则拇指的指向代表该轮的轴向力的方向,从动轮的轴向力方向与主动轮的轴向力方向相反,互为作用与反作用力,即Fa1=-Fa2
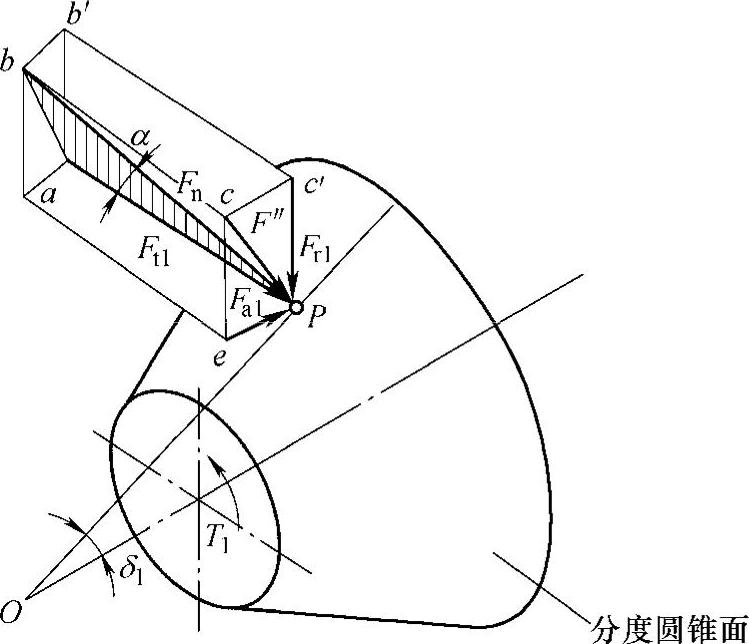
图6-24 直齿锥齿轮传动的受力分析
6.直齿锥齿轮传动的受力分析
当两轴正交(δ1+δ2=90°)时,直齿锥齿轮齿廓在节点P接触的受力情况如图6-24所示。在忽略摩擦力时法向力Fn可分解为圆周力Ft、径向力Fr和轴向力Fa三个分力。
(1)计算公式
Ft=2T1/dm1
Fr1=Fttanαcosδ1
Fa1=Fttanαsinδ1
Fn=Ft/cosα
式中 dm1——小齿轮齿宽中点的分度圆直径,dm1=d1-bsinδ1,b为轮齿宽度,
d1为大端面分度圆直径。
(2)力的方向
1)圆周力Ft的方向在主动轮上与运动方向相反,在从动轮上与运动方向相同,且互为作用与反作用力,即Ft1=-Ft2 。
2)径向力Fr的方向对两轮都是垂直指向各自齿轮的轴线。
3)轴向力Fa的方向对两齿轮均指向各自齿轮的大端。
由于两锥齿轮的轴相互垂直,即δ1+δ2=90°,因此,小齿轮上的径向力和轴向力分别与大齿轮上的轴向力和径向力为作用与反作用力,即Fr1=-Fa2,Fa1=-Fr2。
7.直齿圆柱齿轮传动的强度计算
(1)计算载荷 按名义功率或转矩计算得到的法向载荷Fn称为名义载荷。由于原动机性能及齿轮制造与安装误差、齿轮及支承件变形等因素的影响,实际传动中作用于齿轮上的载荷要比名义载荷大。因此,计算齿轮强度时,通常用计算载荷pc代替名义载荷p,以考虑影响载荷的各种因素。
Pc=KP
K=KAKvKαKβ
式中 K——载荷系数;
KA——使用系数;
Kv——动载系数;
Kα——齿间载荷分配系数;
Kβ——齿向载荷分布系数。
1)使用系数KA。考虑原动机和工作机的运转特性、联轴器的缓冲性能等外部因素引起的动载荷而引入的修正系数,可按表6-54选取。
表6-54 使用系数
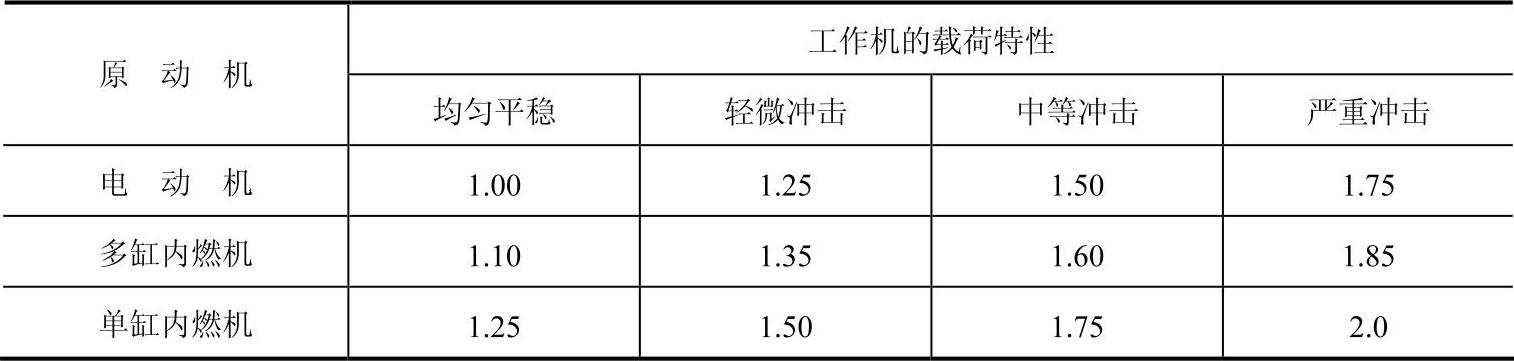
注:对于增速传动可取表中值的1.1倍;当外部机械与齿轮装置之间挠性连接时,其值可适当降低。
2)动载系数Kv。考虑齿轮副在啮合过程中因啮合误差,包括基节误差、齿形误差及轮齿变形等,以及运转速度而引起的内部附加动载荷的影响系数。另外,齿轮在啮合过程中单对齿啮合、双对齿啮合的交替进行,造成轮齿啮合刚度的变化,也要引起动载荷。
对于一般齿轮传动,动载系数Kv值可根据圆周速度及齿轮的制造精度,按图6-25查取;对于直齿锥齿轮传动,在查取动载系数Kv时,应按图中低一级精度线及锥齿轮平均分度圆处的圆周速度vm进行查取。
3)齿间载荷分配系数Kα。齿轮的重合度总是大于1,说明在一对轮齿的一次啮合过程中,部分时间内为两对轮齿啮合,所以理想状态下应该由各啮合齿对均等承载。但对于低精度等级的齿轮传动,实际情况并非如此,它受制造精度、轮齿刚度、齿轮啮合刚度、修缘量、跑合量等多方面因素的影响。齿间载荷分配系数Kα是用于考虑制造误差和轮齿弹性变形等原因使两对同时啮合的轮齿上载荷分配不均的影响而引进的修正系数。对一般不需作精确计算的直齿轮传动,可假设为单齿对啮合,故取Kα=1;对斜齿圆柱齿轮传动,可取Kα=1~1.4,精度低、齿面硬度高时取大值,反之取小值。
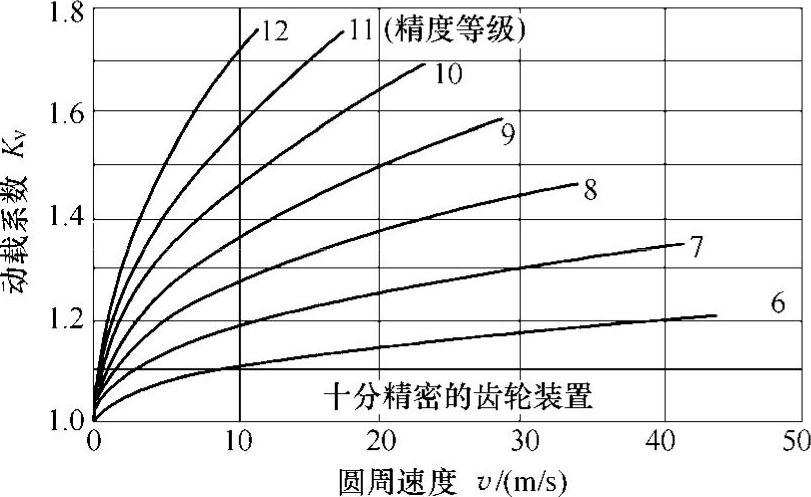
图6-25 动载系数Kv
4)齿向载荷分布系数Kβ。由制造误差引起的齿向误差、齿轮及轴的弯曲和扭转变形、轴承和支座的变形及装配误差等,而导致轮齿接触线上各接触点间载荷分布不均匀,为此引入齿向载荷分布系数Kβ,用于考虑实际载荷沿轮齿接触线分布不均的影响,其值的大小主要受齿轮相对轴承配置形式、齿宽系数(b/d1)及齿面硬度的影响。对于一般的工业用圆柱齿轮可按图6-26查取;对于直齿锥齿轮,齿向载荷分布系数Kβ=1.1~1.3。
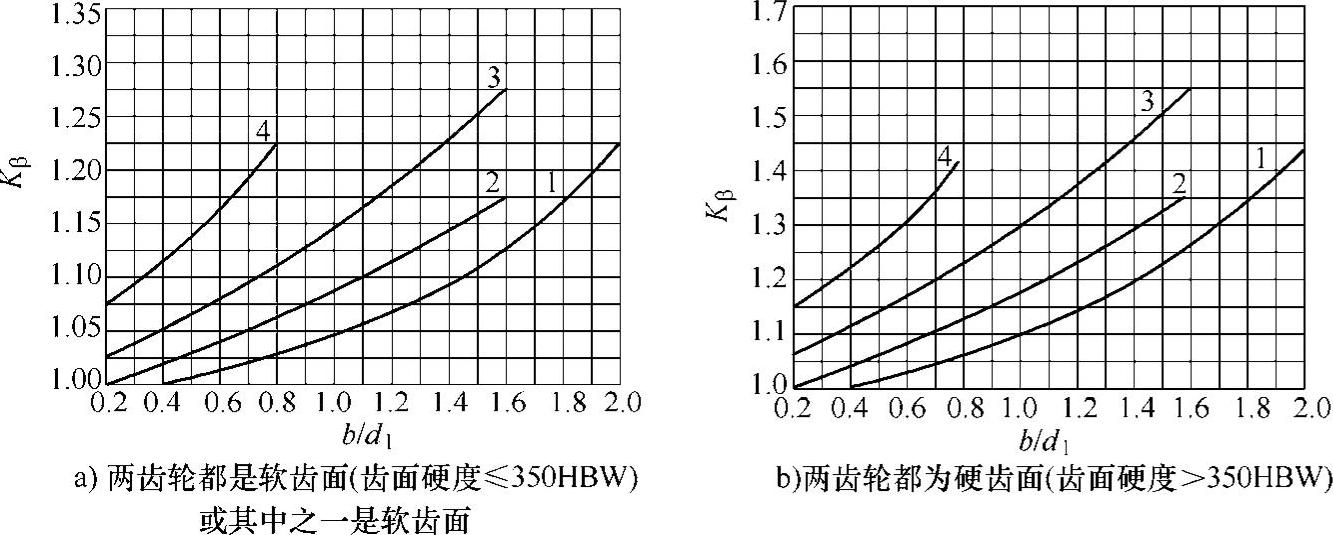
图6-26 齿向载荷分布系数Kβ
1—齿轮在两轴承间对称布置 2—齿轮在两轴承间非对称布置,轴的刚度较大 3—齿轮在两轴承间非对称布置,轴的刚度较小 4—齿轮悬臂布置
(2)标准直齿圆柱齿轮齿根弯曲疲劳强度计算 由于齿轮轮缘的刚度很大,在弯曲疲劳强度计算时,可将轮齿看成宽度为b的悬臂梁,力集中作用在齿宽中面上,如图6-27所示。
1)假设条件
①轮齿视为悬臂梁,其长为l、宽为b。
②为了简化计算,认为法向力Fn全部作用在一个轮齿的齿顶。
③载荷由一对齿承担,考虑理论上载荷应由同时啮合的多对齿分担,可用重合度系数Yε对齿根弯曲应力进行修正。
齿根处的危险截面的确定:确定危险截面的方法有很多,其中30°切线法最为简单实用,即作与轮齿对称中心线成30°夹角并与齿根过渡圆角相切的斜线,则认为两切点连线是危险截面位置。
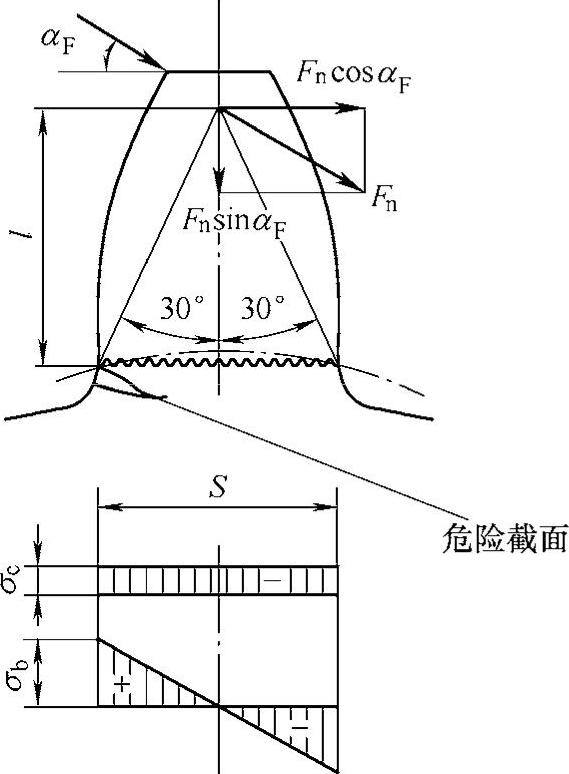
图6-27 齿根弯曲应力
2)齿根弯曲疲劳强度计算。作用到齿顶的法向力Fn可分解为相互垂直的两个力:FncosαF和FnsinαF。FncosαF 移到齿根危险截面是一个剪切力和弯矩,使齿根危险截面受剪和受弯,产生切应力和弯曲应力σb;FnsinαF使齿根危险截面受压而产生压应力σc。因为切应力和压应力之和不足弯曲应力σb的5%,因此可忽略不计(在应力修正系数中考虑),所以齿根总的应力近似等于齿根弯曲应力。
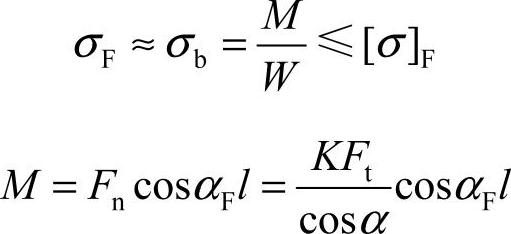
则
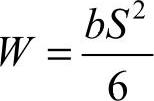
校核式为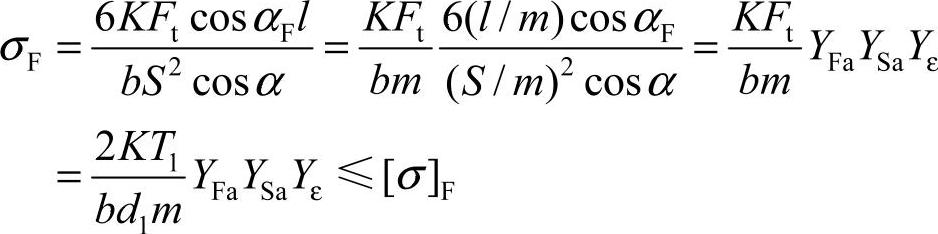
以上为齿根弯曲疲劳强度的校核式。
将b=Ψdd1、d1=mz1 代入得齿根弯曲疲劳强度的设计式,则有
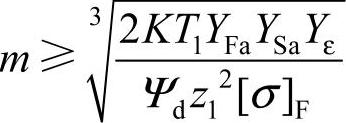
式中 αF——齿顶压力角(°);
α——分度圆压力角(°);
b——齿宽(mm);
m——齿轮的模数(mm);
YFa——齿形系数;
YSa——应力修正系数;
Yε——重合度系数。
T1——小齿轮的转矩(9.55×106N·mm);
Ψd——齿宽系数;
z1——小齿轮的齿数;
[σ]F——许用弯曲应力(MPa)。
3)公式说明①设计齿轮时,一对齿轮相啮合,大小齿轮的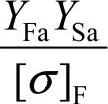 不同,取
不同,取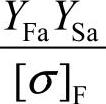 大者代入更安全;计算出的模数m必须圆整到标准值,传递动力时m≥1.5~2mm。 ②齿形系数YFa。
大者代入更安全;计算出的模数m必须圆整到标准值,传递动力时m≥1.5~2mm。 ②齿形系数YFa。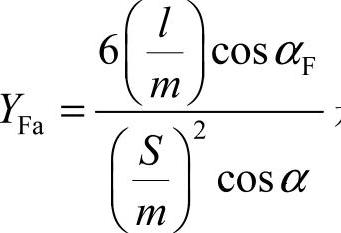 是无量纲的数,表示轮齿的几何形状对抗弯能力的影响系数,只取决于齿形(齿数z及变位系数X影响齿形),与模数m无关。YFa越小,抗弯强度越高。随着齿数的增加,YFa减小,如图6-28所示。
是无量纲的数,表示轮齿的几何形状对抗弯能力的影响系数,只取决于齿形(齿数z及变位系数X影响齿形),与模数m无关。YFa越小,抗弯强度越高。随着齿数的增加,YFa减小,如图6-28所示。
③应力修正系数YSa。应力修正系数YSa综合考虑齿根圆角处应力集中和除弯曲应力以外其余应力对齿根应力的影响,随着齿数的增加,YSa增加。与齿数z、变位系数X有关,YSa值可参考图6-29查取。
值得注意的是,随着齿数增加,YFa与YSa乘积减小,因此在模数一定时,齿数增加对弯曲强度是有益的。
④重合度系数Yε。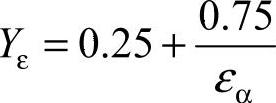 ,εα为端面重合度。
,εα为端面重合度。
⑤齿宽系数Ψd。Ψd=b/d1,通常轮齿愈宽,承载能力也愈高,因而轮齿不宜过窄;但增大齿宽又会使齿面上的载荷分布更趋不均匀,故应适当选取齿宽系数。其推荐值可按表6-55选取,它取决于齿面硬度和齿轮相对于轴承的位置。
⑥模数m。计算出的模数应圆整为标准值,对于传递动力的齿轮,其模数不应低于1.5mm。因为s=πm/2,模数增加,齿厚增加,整个轮齿各处厚度增加,则抗弯截面模量增加,工作应力减小,弯曲强度增高;反之模数小,弯曲强度低。所以说模数决定弯曲强度的主要因素。
开式传动:将计算出的模数m增大10%~15%以考虑磨损的影响。
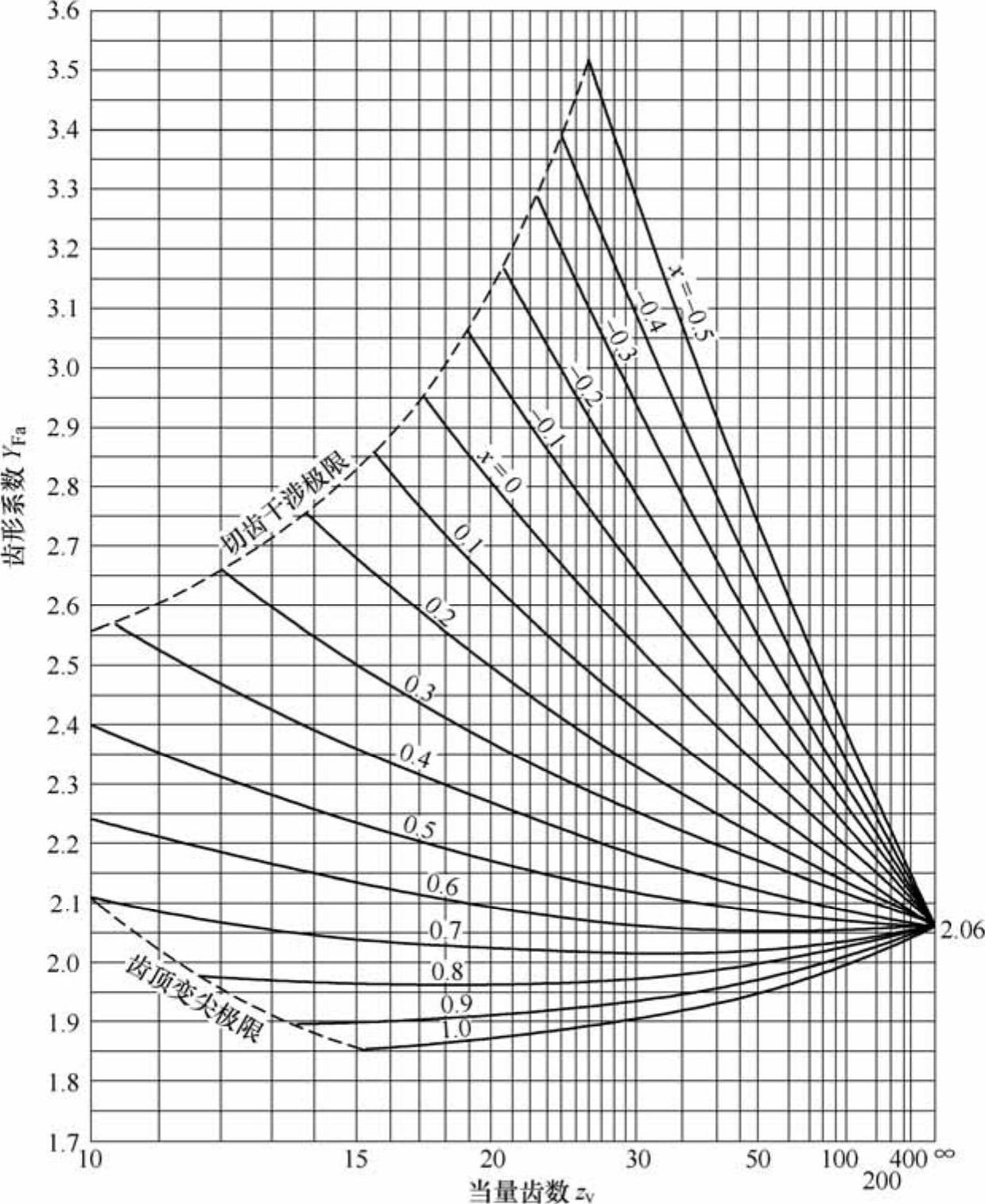
图6-28 外齿轮齿形系数YFa
αn=20°,han=1mn,cn=0.25mn,ρf=0.38mn;对于内齿轮,可取YFa=2.053。
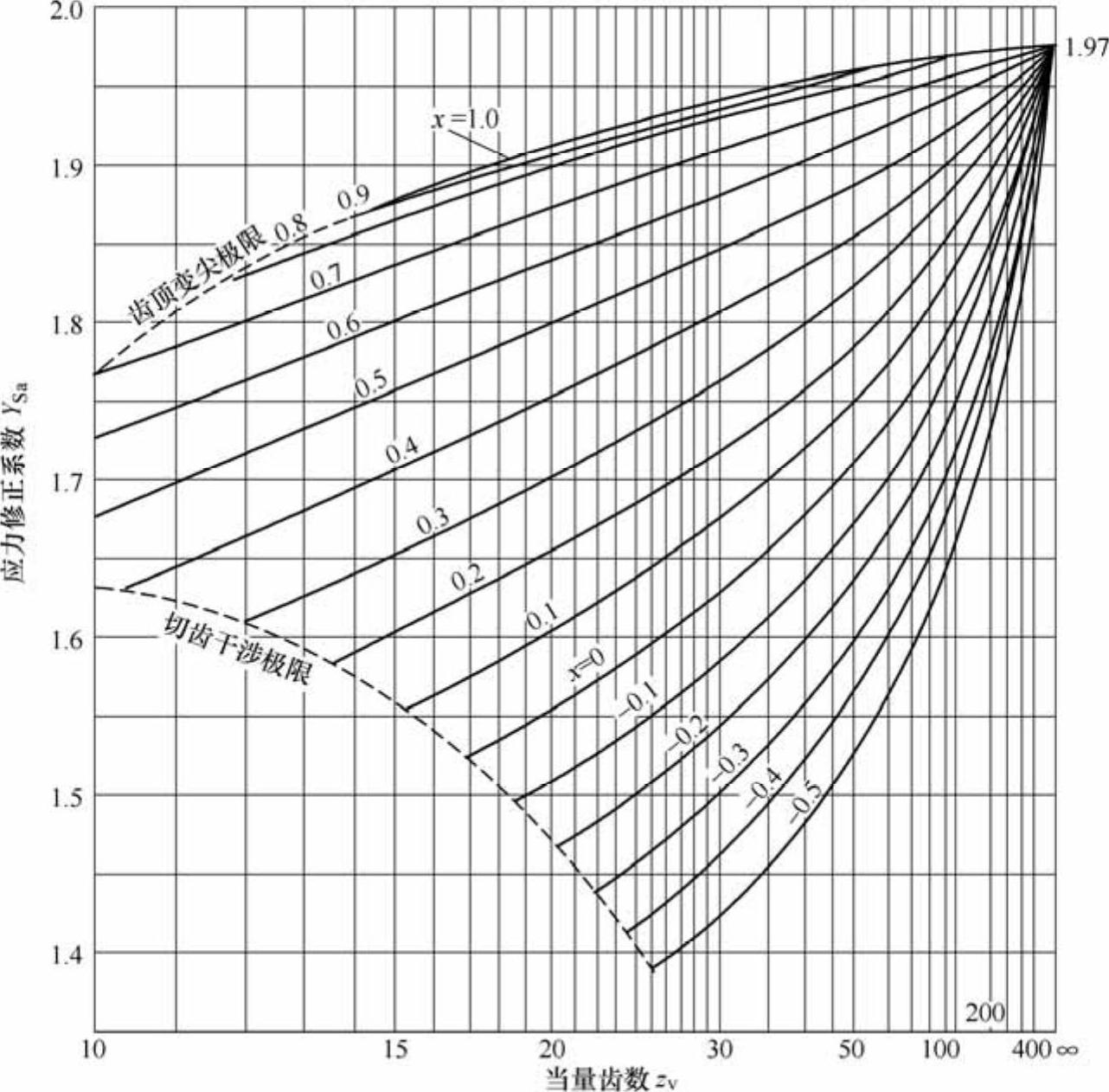
图6-29 外齿轮应力修正系数YSaαn=20°,han=1mn,cn=0.25mn,ρf=0.38mn;对于内齿轮,可取YSa=2.65。(www.daowen.com)
表6-55 齿宽系数Ψd
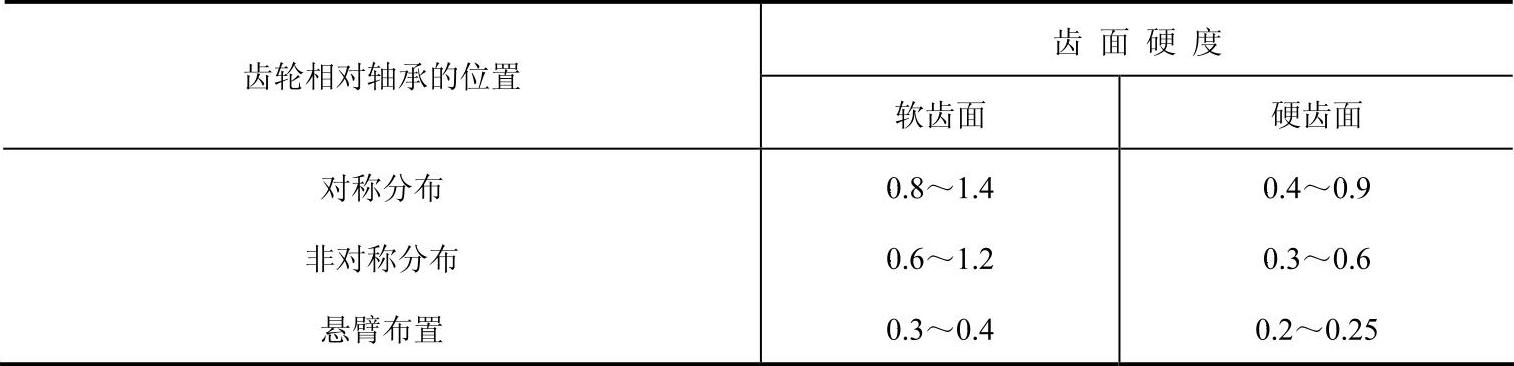
注:1.直齿圆柱齿轮宜取较小值,斜齿轮可取较大值。
2.载荷稳定、轴刚性大时取较大值;变载荷、轴刚性较小时宜取较小值。
⑦小齿轮齿数z1的选择。对于闭式软齿面齿轮,尽量选用小模数、多齿数,通常选z1=20~40;开式、硬齿面的齿轮为了防止意外断齿,可选大一些的模数,齿数只要不根切即可,z1≥17。
⑧许用弯曲应力[σ]F
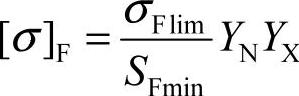
式中 YN——寿命系数,齿轮为有限寿命时许用弯曲应力提高的系数。其值取
决于工作应力循环次数NL(见图6-30);
YX——尺寸系数,当m≤5时取1。其值取决于齿轮的模数和材料,可查
图6-31;
SFmin——弯曲强度的最小安全系数,查表6-56;
σFlim——失效率1%时,试验齿轮的齿根弯曲疲劳强度极限,可查图6-32。
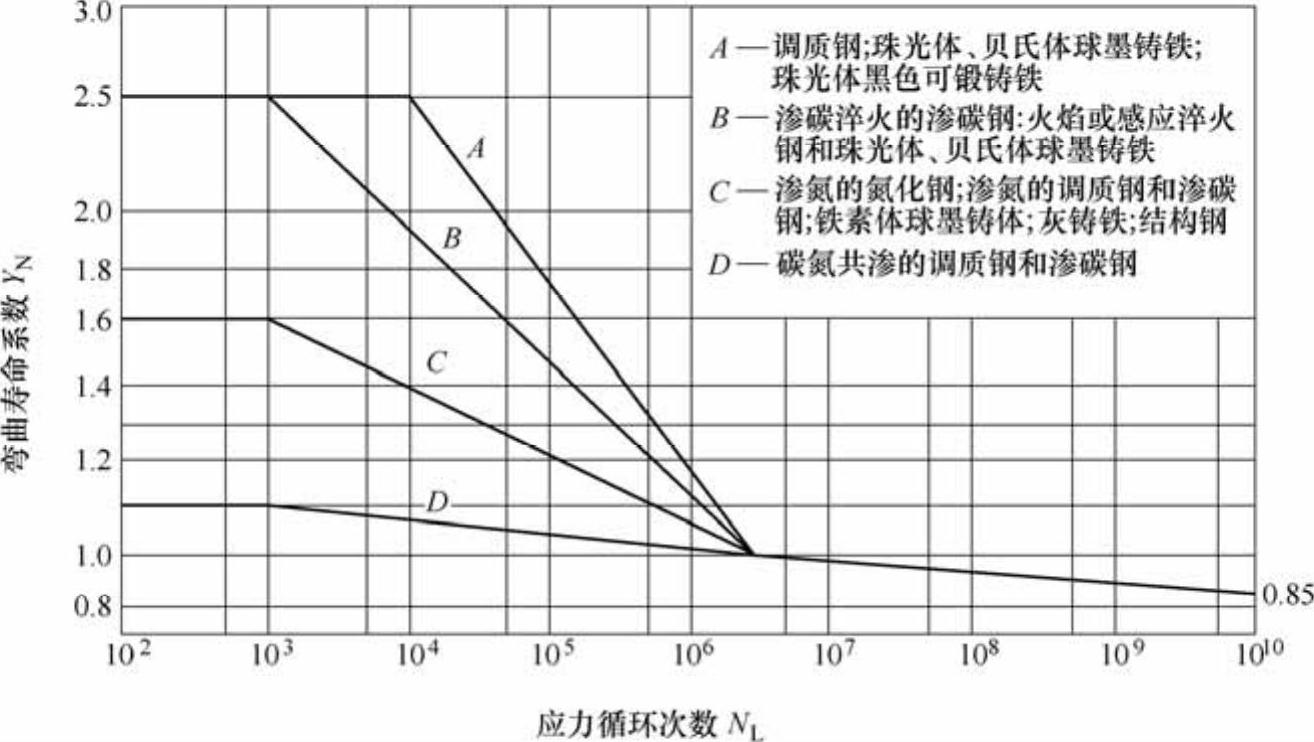
图6-30 弯曲寿命系数YN
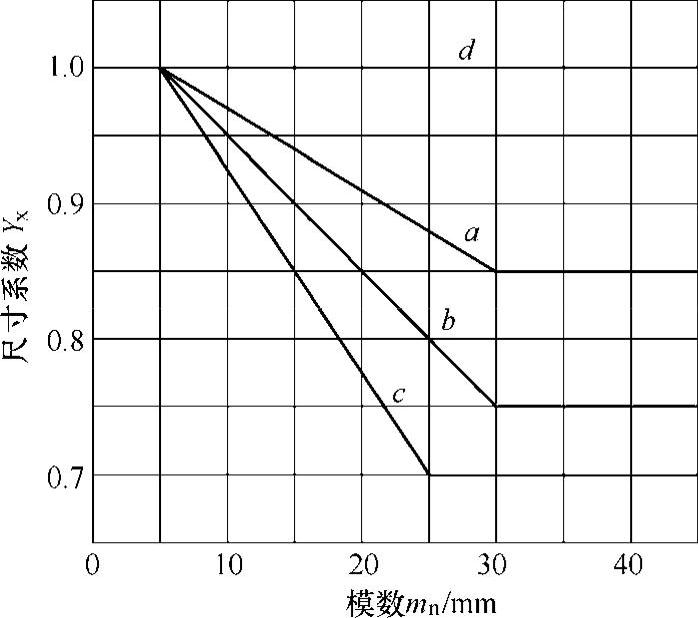
图6-31 弯曲强度计算的尺寸系数YX
表6-56 弯曲强度的最小安全系数参考值
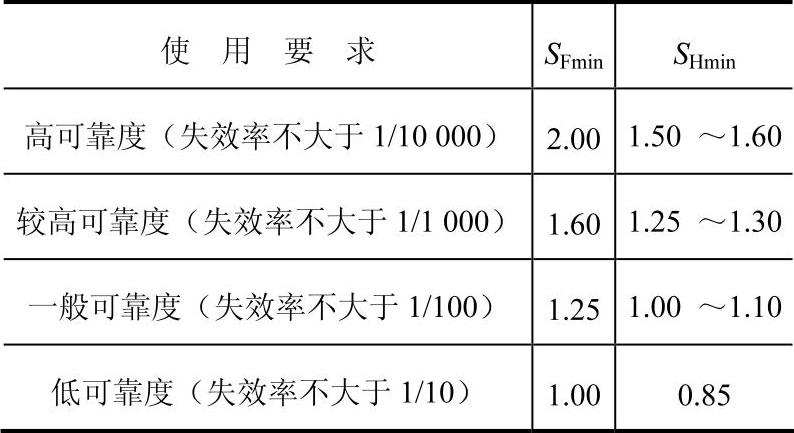
注:在经过使用验证或材料强度、载荷工况及制造精度
拥有较准确的数据时,SHmin可取下限。
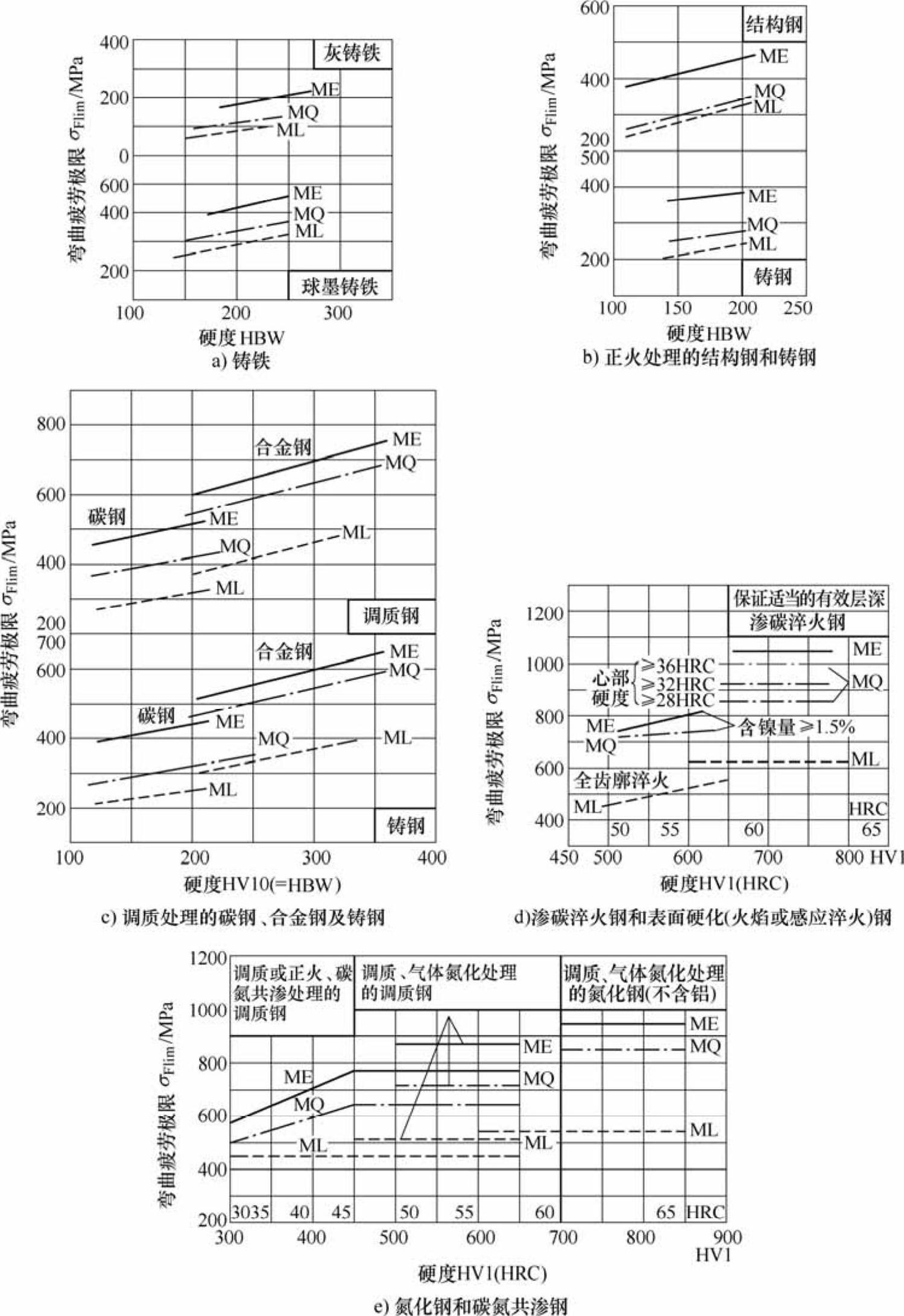
图6-32 试验齿轮的齿根弯曲疲劳强度极限σFlim
(3)标准直齿圆柱齿轮传动齿面接触疲劳强度计算 齿面疲劳点蚀与齿面接触应力的大小有关,最易发生在齿根部分靠近节线处,为计算方便,通常取节点处的接触应力作为计算依据,如图6-33所示。
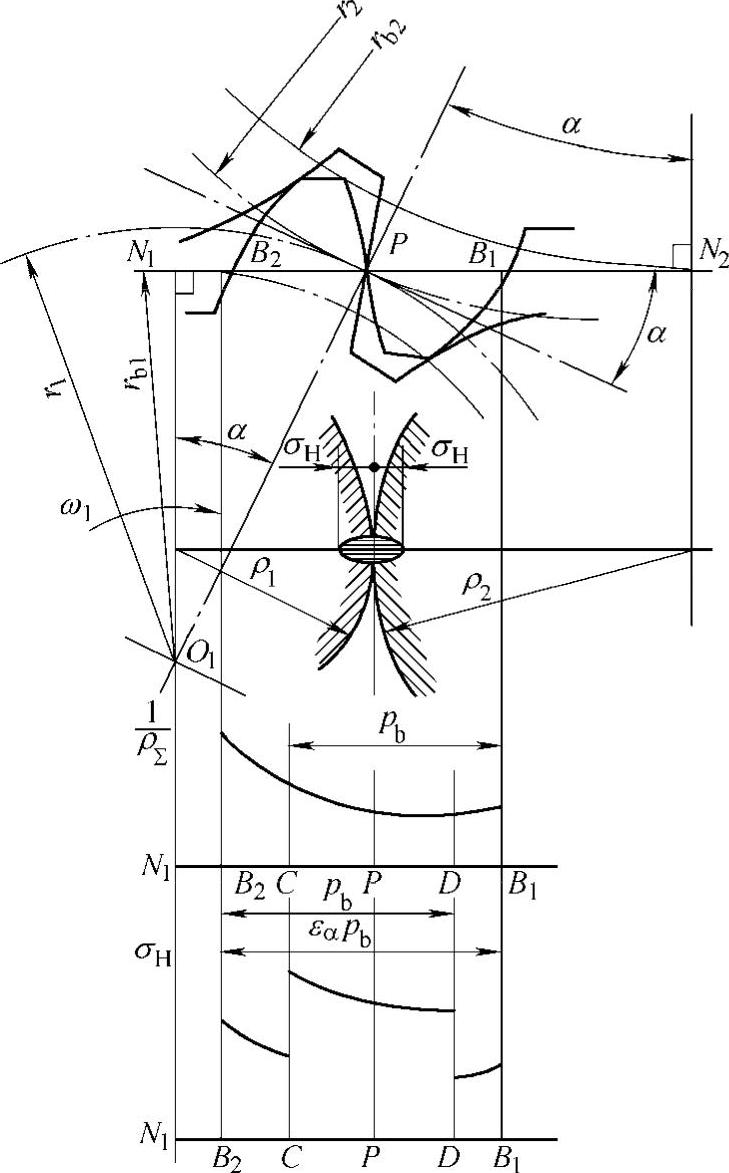
图6-33 齿面接触应力
利用两圆柱赫芝公式,代入齿轮的参数,并进行简化处理,引进若干系数,得出节点处的接触应力,进而得出齿面接触疲劳强度的校核公式
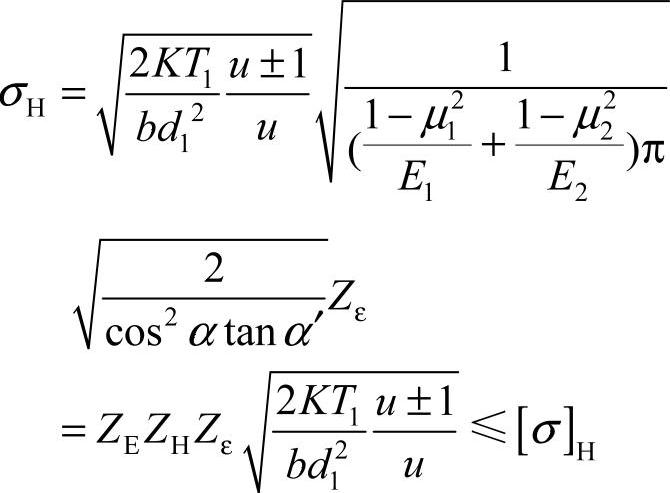
将齿宽系数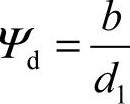 引入上式,得出设计式为
引入上式,得出设计式为
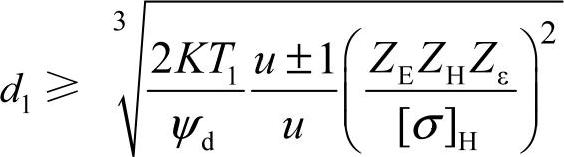
正号用于外啮合,负号用于内啮合。
式中 ZE——材料的弹性系数,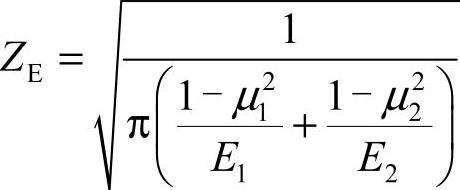 ;
;
μ1,μ2——两齿轮材料的泊松比;
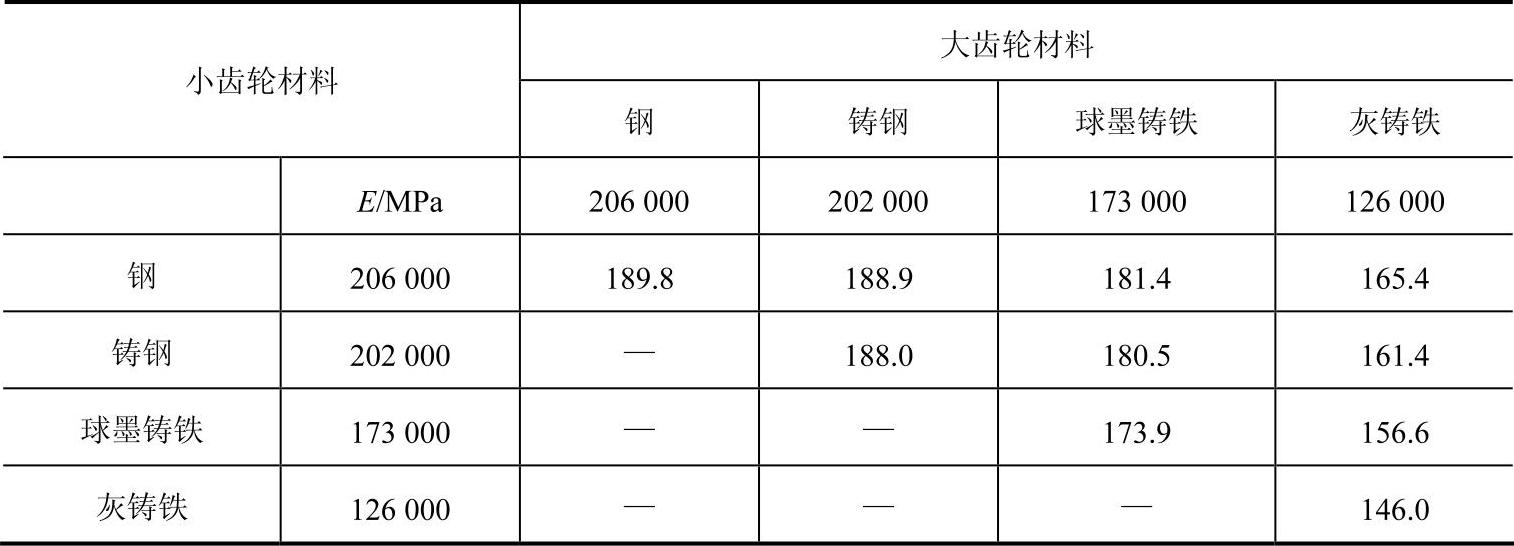
E1,E2——两齿轮材料的弹性模量,设计时可查表6-57;
Zε——重合度系数,代表重合度对接触应力的影响系数,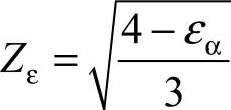 ,
,
εα为重合度;
ZH——节点区域系数,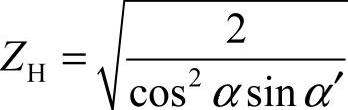 ,考虑节点处齿廓曲率对接触
,考虑节点处齿廓曲率对接触
应力的影响,对于标准齿轮(α=20°),按标准中心距安装时,节点区域系数ZH为2.5;
d1——小齿轮的分度圆直径;
[σ]H——许用应力,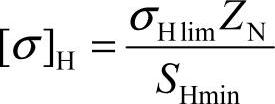 。σHlim为失效率为1%时,试验齿轮的接触疲劳极限,查图6-34;SHmin为齿面接触强度最小安全系数安全系数,见表6-56。因弯曲疲劳造成的轮齿折断有可能引起重大事故,而接触疲劳产生的点蚀只影响使用寿命,故轮齿弯曲疲劳安全系数SFmin的数值远大于齿面接触疲劳安全系数SHmin;ZN为接触疲劳强度计算的寿命系数,取决于工作应力循环次数NL,查图6-35。
。σHlim为失效率为1%时,试验齿轮的接触疲劳极限,查图6-34;SHmin为齿面接触强度最小安全系数安全系数,见表6-56。因弯曲疲劳造成的轮齿折断有可能引起重大事故,而接触疲劳产生的点蚀只影响使用寿命,故轮齿弯曲疲劳安全系数SFmin的数值远大于齿面接触疲劳安全系数SHmin;ZN为接触疲劳强度计算的寿命系数,取决于工作应力循环次数NL,查图6-35。
表6-57 材料的弹性模量ZE (单位:MPa)
8.斜齿圆柱齿轮传动的强度计算
(1)斜齿圆柱齿轮的当量齿轮 以该斜齿轮的法面模数mn为当量齿轮的模数,以r/cos2
ρV=r/cos2β为当量分度圆半径(其中r=mtz/2),以zV=z/cos3β为当量齿数,所做的直齿圆柱齿轮即为该斜齿圆柱齿轮的当量齿轮。
(2)斜齿圆柱齿轮的弯曲疲劳强度计算公式 斜齿圆柱齿轮传动的强度计算利用其当量齿轮直接套用直齿圆柱齿轮的强度计算公式进行的。但是由于斜齿轮存在螺旋角,使其重合度较大,接触线较长,当量齿轮的分度圆半径也较大,因此斜齿轮的弯曲应力和接触应力比直齿轮有所降低,可引进螺旋角系数Yβ(或Zβ),于是可得斜齿轮强度计算公式。
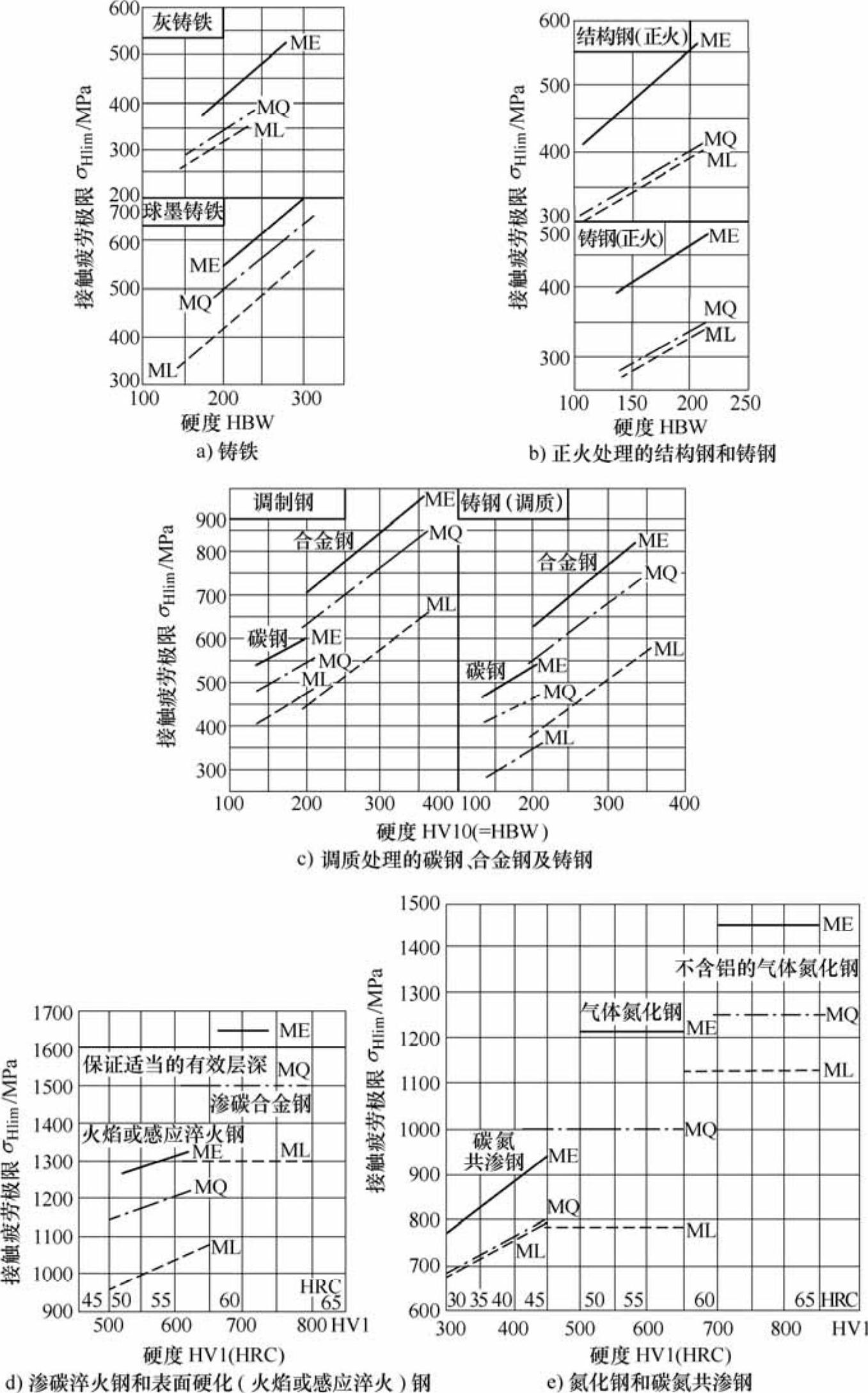
图6-34 试验齿轮的接触疲劳极限σHlim
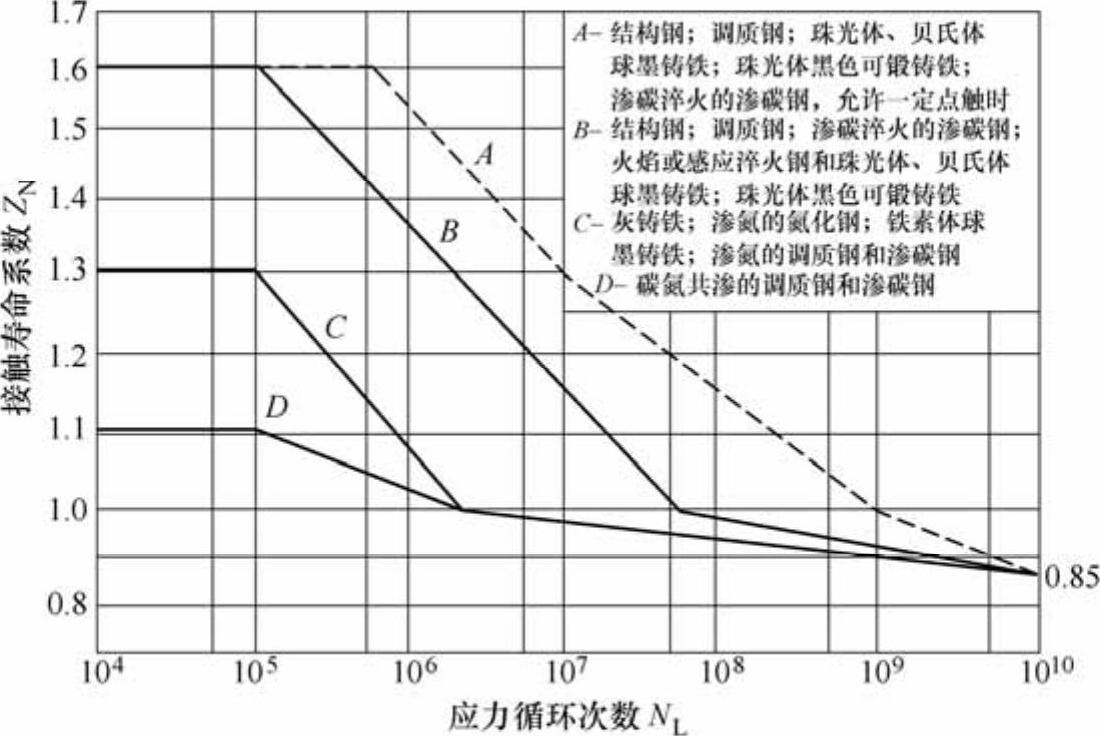
图6-35 接触寿命系数ZN
1)轮齿弯曲疲劳强度的验算公式为
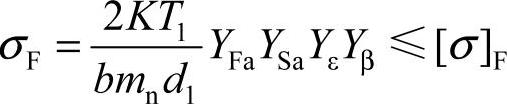
2)轮齿弯曲疲劳强度的设计公式为

式中 Yβ——螺旋角系数,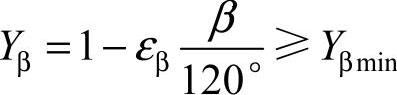 ,
,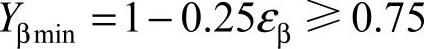 ,当εβ≥1时,按εβ=1计算;若Yβ≤0.75,则取Yβ=0.75;当β>30o时,按β=30o计值;
,当εβ≥1时,按εβ=1计算;若Yβ≤0.75,则取Yβ=0.75;当β>30o时,按β=30o计值;
YFa——齿形系数,应根据当量齿数zV=z/cos3β查图6-28;
YSa——应力修正系数,应根据当量齿数zV=z/cos3β查图6-29;
Yε——重合度系数,可套用直齿轮的公式计算,但应代以当量齿轮的端面重合度。
(3)斜齿圆柱齿轮的齿面接触疲劳强度计算公式
1)齿面接触疲劳强度的验算公式:
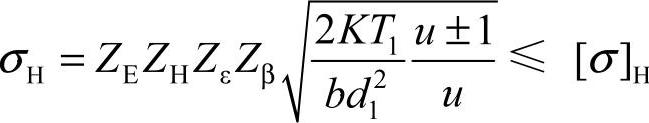
2)齿面接触疲劳强度的设计公式:
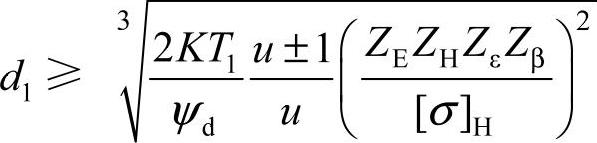
式中 Zε——重合度系数,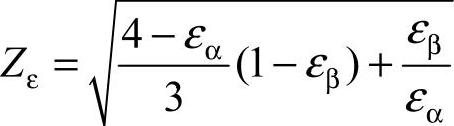 ,εα及εβ分别为端面重合度和轴向重合度; Zβ——螺旋角系数,
,εα及εβ分别为端面重合度和轴向重合度; Zβ——螺旋角系数,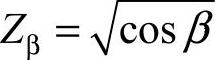 ,β为分度圆上的螺旋角;
,β为分度圆上的螺旋角;
ZH——节点区域系数ZH,对于法面压力角αn =20°的标准齿轮可查图6-36。其余符号同直齿轮。
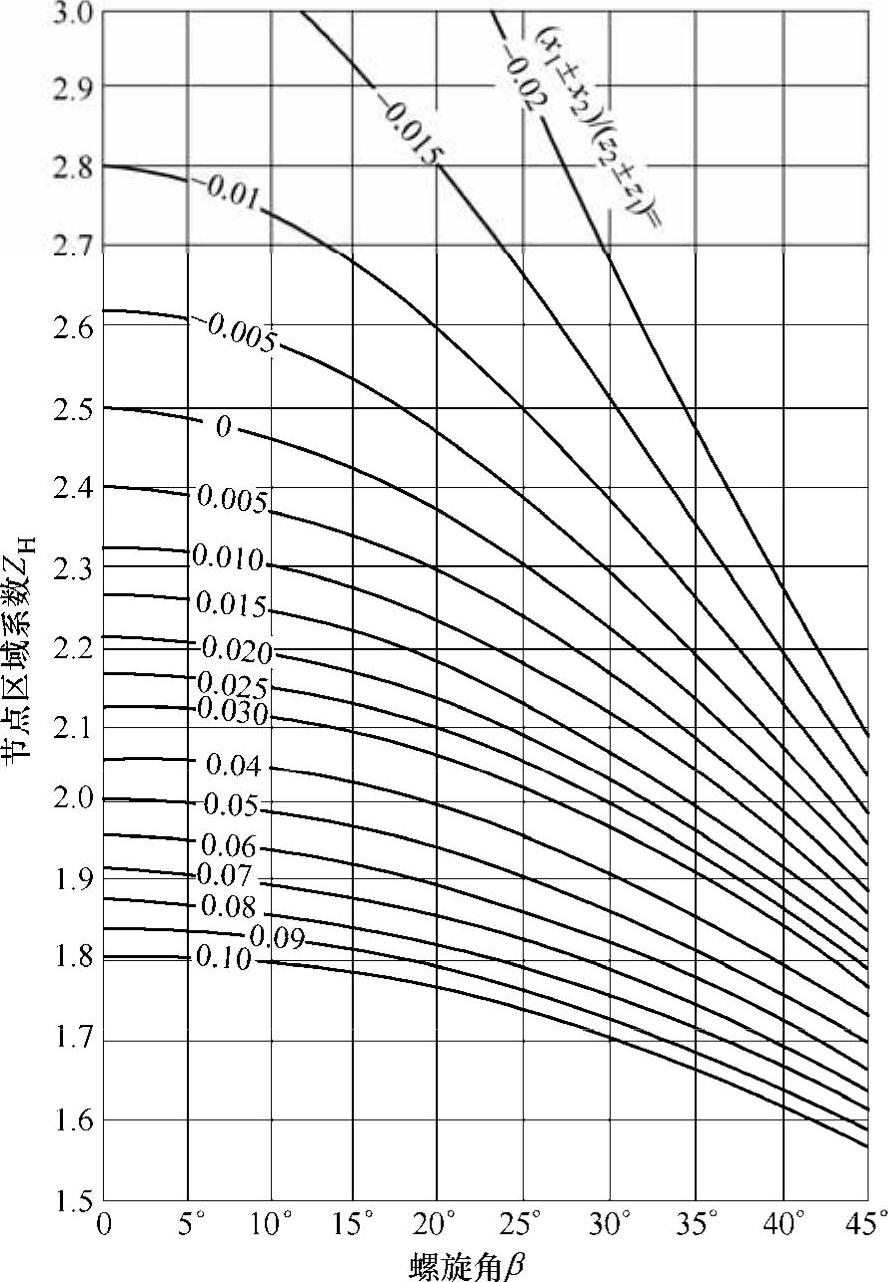
图6-36 节点区域系数ZH
9.直齿锥齿轮传动的强度计算
锥齿轮是用于两相交轴之间的传动,两轴交角可根据需要决定,齿轮根据轮齿形状分为直齿、斜齿和曲齿,本文介绍两轴正交的标准直齿圆锥传动的强度计算方法。
(1)齿宽中点处的当量齿轮 将锥齿轮齿宽中点处的背锥展成平面扇形,并取锥齿轮平均模数mm和标准压力角α,将两扇形补足为完整的圆柱齿轮,该直齿圆柱齿轮即为齿宽中点处的当量齿轮。引入齿宽系数ΨR=b/R,可得当量齿轮与锥齿轮大端面之间的参数关系。
1)当量齿轮分度圆直径dv1、dv2为
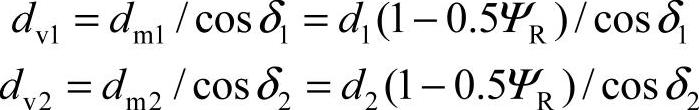
式中 dm1,dm2——小齿轮和大齿轮的齿宽中点处的分度圆直径;
δ1,δ2——小齿轮和大齿轮的分锥角;
ΨR——齿宽系数,ΨR=b/R。由于锥齿轮两端轴承很难对称布置,多为悬臂,载荷分布不均现象较为严重,因此宽度b不能过大,一般取齿宽系数ΨR=0.25~0.35,最常用的值为1/3。
2)当量齿数Zv1、Zv2为
zv1=z1/cosδ1;zv2=z2/cosδ2
3)当量齿轮的模数(即齿宽中点处的模数mm)为
mm=m(1-0.5ΨR)
式中 m——大端模数。
4)当量齿轮的齿数比uv为
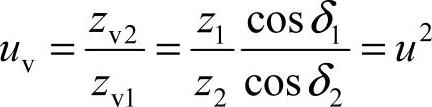
式中 u——实际齿数比。
(2)直齿锥齿轮传动的强度计算 直齿锥齿轮传动的强度与齿宽中点处的当量齿轮等强度,计算可依据其齿宽中点的当量齿轮套用直齿圆柱齿轮的强度计算公式,再将参数转换成大端参数而得到计算公式。但考虑齿面接触区长短对应力的影响,取有效宽度为0.85b。
1)齿根弯曲疲劳强度计算公式。
校核式
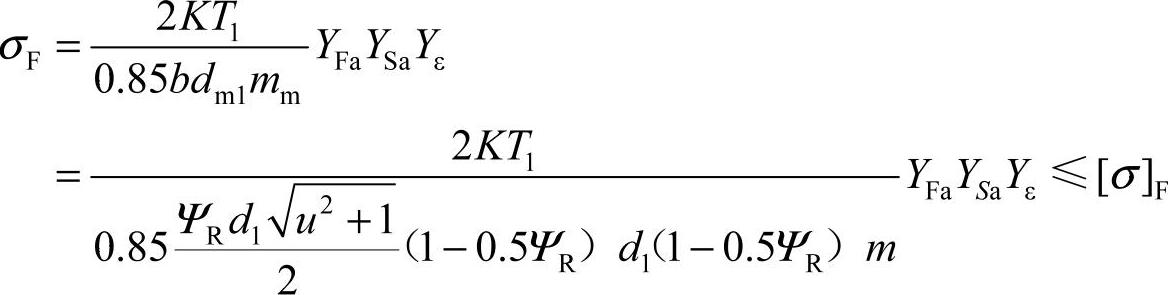
即
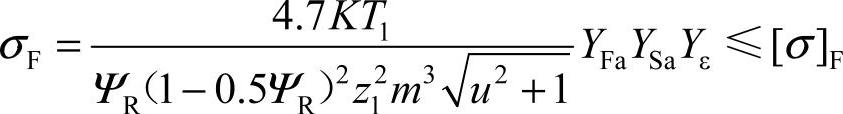
设计式
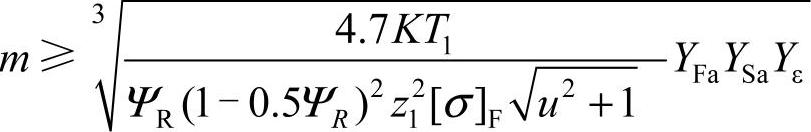
式中 YFa,YSa——齿形系数YFa和应力修正系数YSa,在选取这两个系数时,按当量齿数zv=z/cosδ分别查图6-37和图6-38;
K——载荷系数,K=KAKVKαKβ,其中使用系数KA的查取与直齿圆柱齿轮相同;动载系数KV按齿宽中点圆周速度,精度等级最好按低一级的公差查图6-25;齿间载荷分配系数Kα=1;齿向载荷分布系数Kβ=1.1~1.3。
其他参数的意义及选取与直齿圆柱齿轮相同。
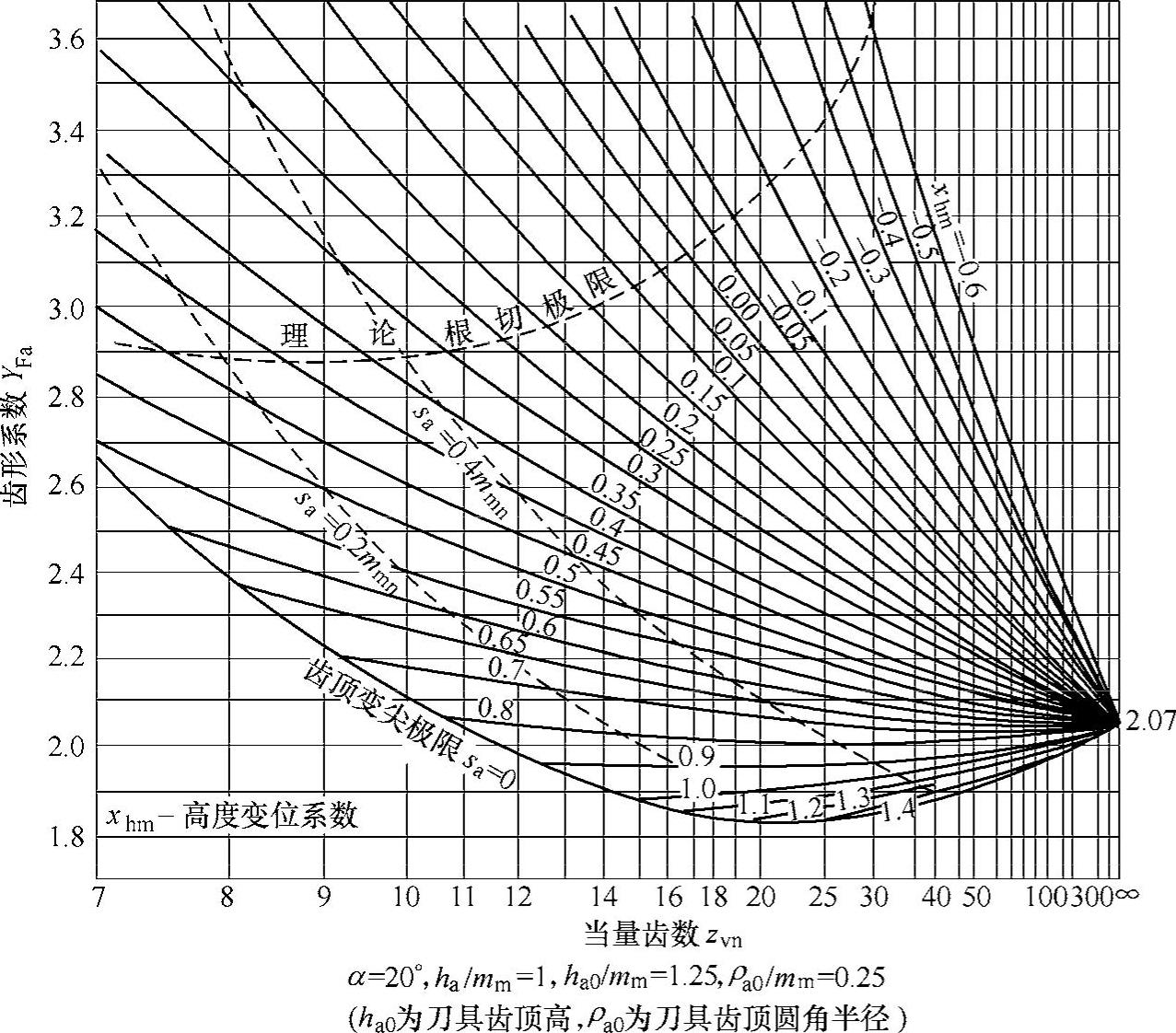
图6-37 齿形系数YFa
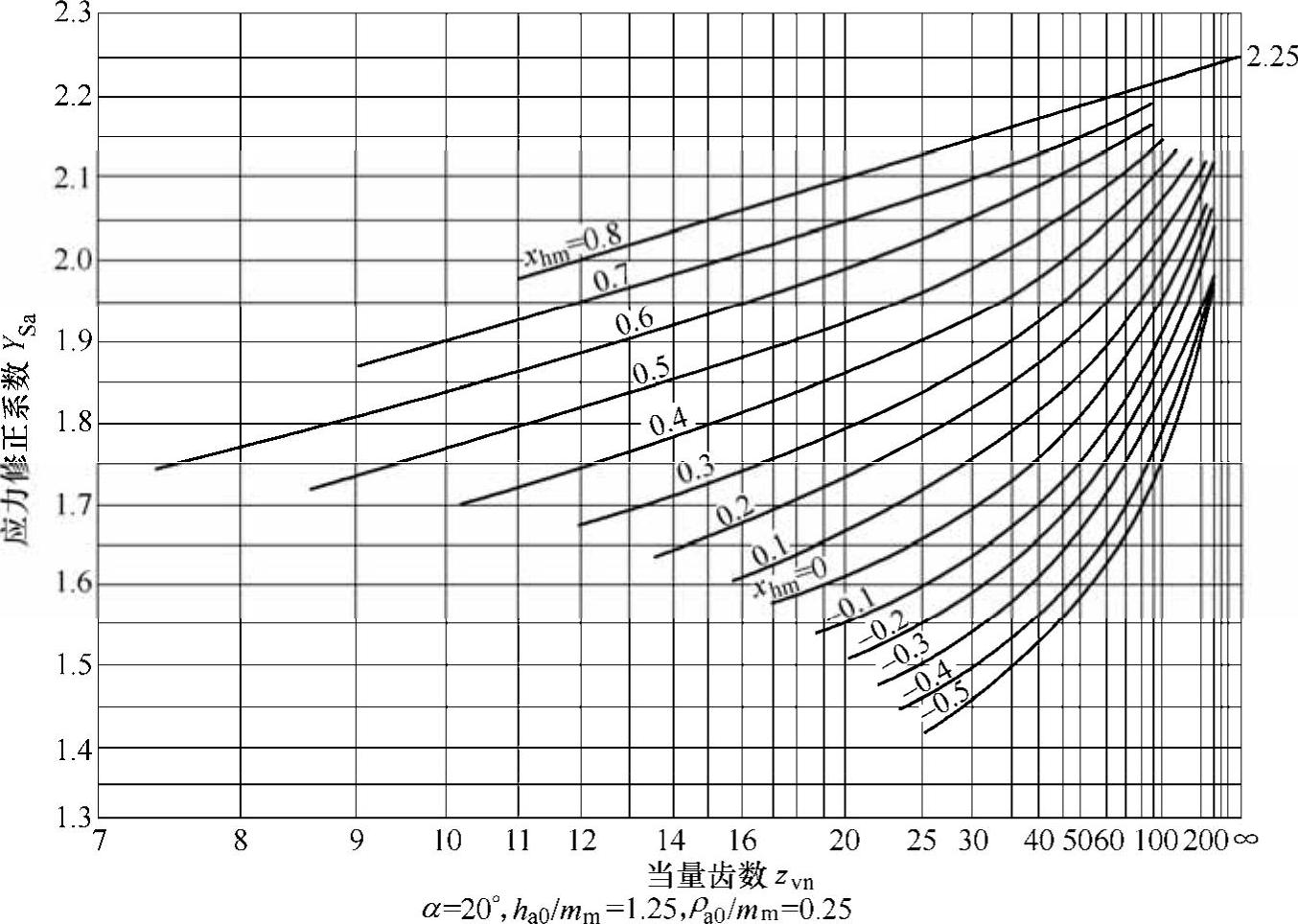
图6-38 应力修正系数YSa
2)齿面接触疲劳强度计算公式。同样取有效宽度0.85b,按齿宽中点的当量齿轮套用直齿圆柱齿轮可得接触疲劳强度计算公式。
直齿锥齿轮的齿面接触疲劳强度计算公式如下。
校核式

设计式
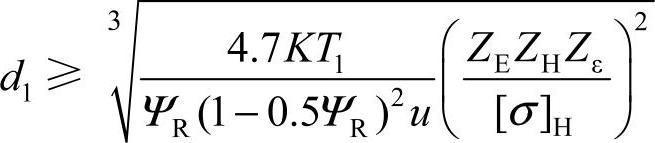
式中 ZH——节点区域系数,按β=0,αn=20°查图6-36;
Zε——重合度系数,可套用直齿圆柱齿轮的公式,但按当量齿轮重合度εαv计算。
弹性系数ZE、许用接触应力[σ]H、接触疲劳极限应力σHlim与直齿圆柱齿轮完全相同。
10.齿轮的结构设计
通过齿轮传动的强度计算,只能确定出齿轮的主要尺寸,如分度圆直径、模数、齿数、齿宽、螺旋角等,而轮缘、轮毂、轮辐等的结构型式及尺寸不是要求十分精确,通常是由结构设计确定。
结构设计通常先按强度计算求出齿轮的直径大小,综合考虑加工方法、经济性、几何尺寸、毛坯、材料等因素,进行结构设计。结构设计一般是根据经验公式进行设计计算的,因为有些尺寸要求不是十分精确,因此所得的计算值一般应进行圆整以便于加工和测量。齿轮的结构大致可分以下几种型式。
(1)齿轮轴 对于直径较小的钢制齿轮,当为圆柱齿轮时,齿根圆到键槽底部的距离e<2mt(mt为端面模数);当为锥齿轮时,若按小端尺寸计算而得的e<1.6m,如图6-39所示,可将齿轮和轴做成一体,称为齿轮轴,如图6-40所示。这时齿轮与轴必须采用同一种材料制造。若e值超过上述尺寸时,即齿轮的直径比轴的直径大得多,则应把齿轮和轴分开制造。
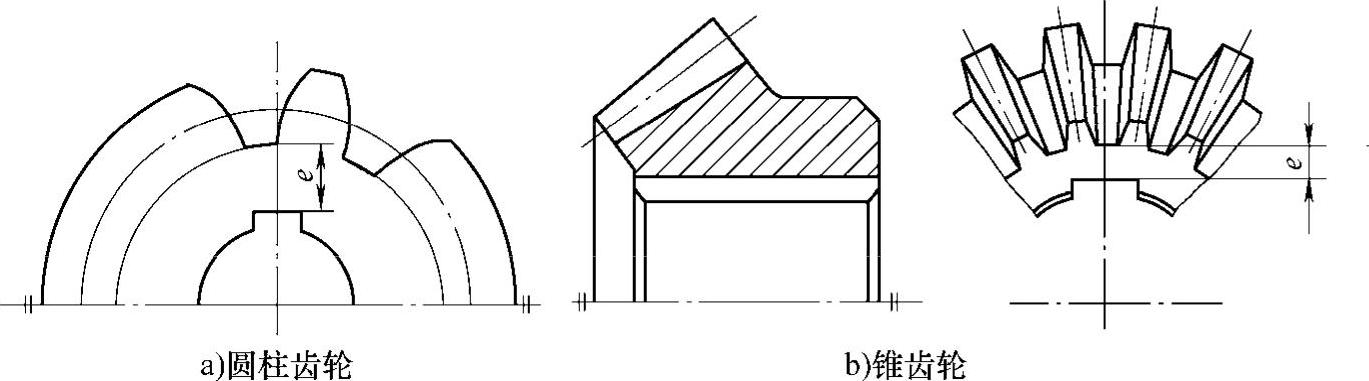
图6-39 齿轮的结构尺寸e
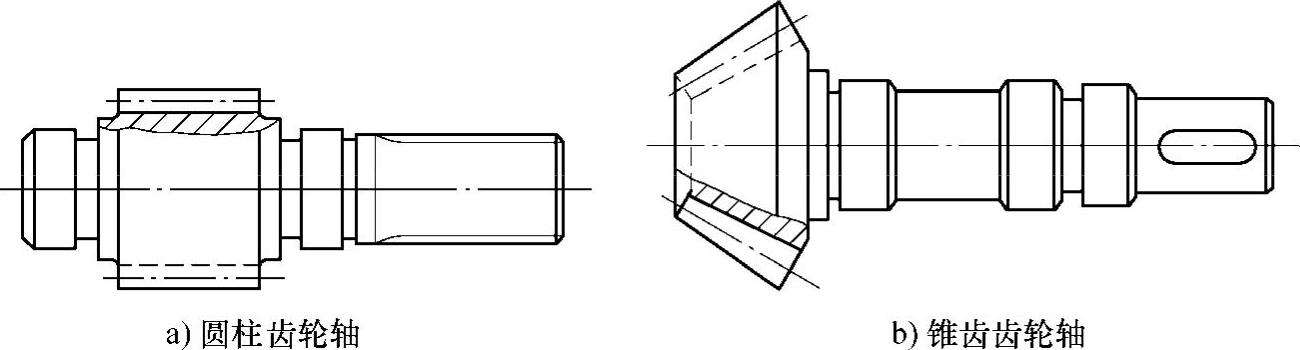
图6-40 齿轮轴
(2)实心结构齿轮 当齿顶圆直径da≤160mm时,齿轮可做成如图6-41所示的实心结构。在航空工业产品中也有做成腹板式结构的。
(3)腹板式结构齿轮 当齿顶圆直径da≤500mm时,齿轮一般是锻造的,如图6-42所示。当批量生产、性能要求不高时,也可以是铸造的,通常采用如图6-43所示的腹板式结构或孔板结构。
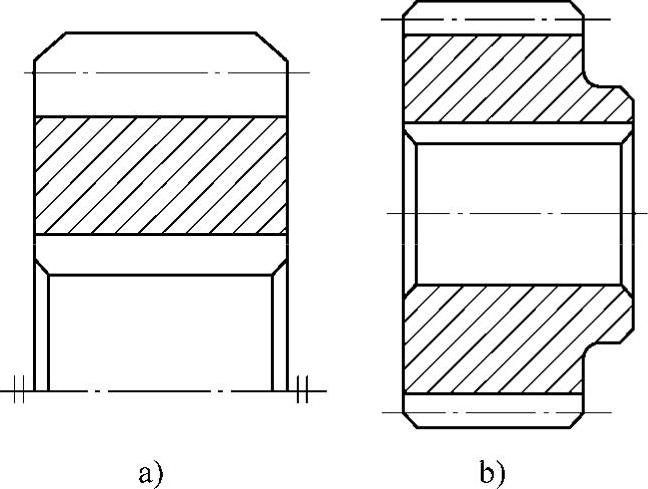
图6-41 实心结构齿轮
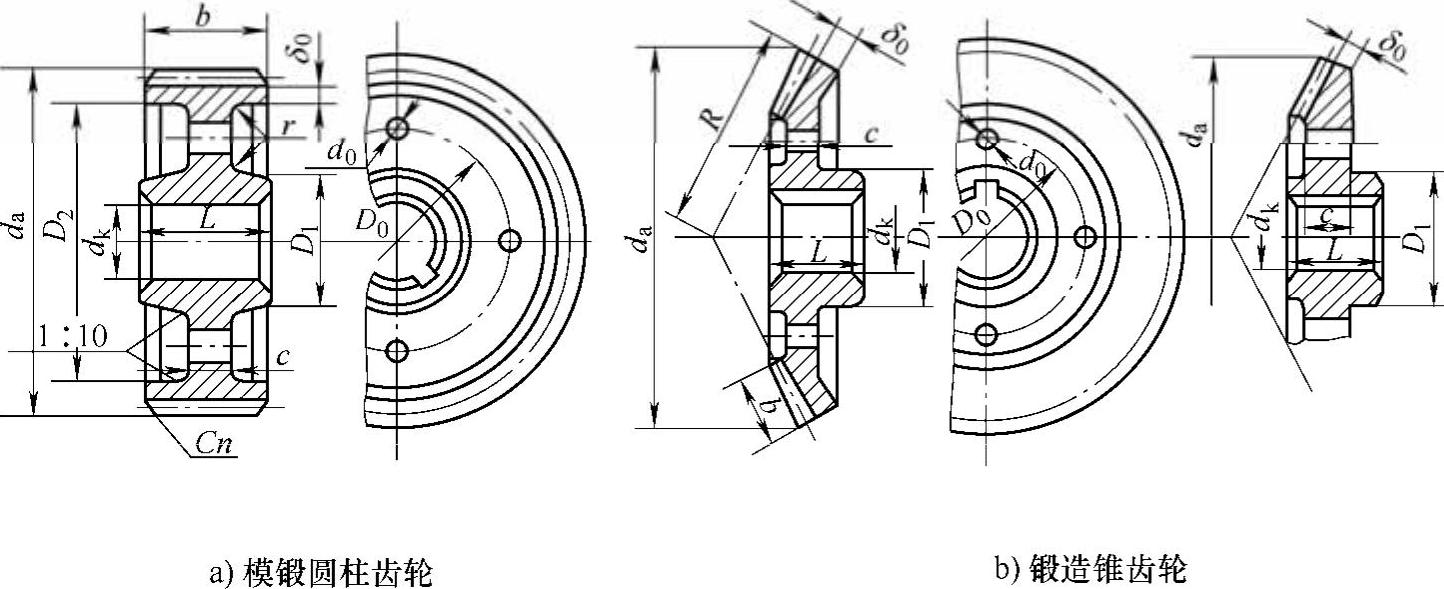
图6-42 腹板式锻造结构齿轮
注:1.图a)自由锻圆柱齿轮无拔模斜度,其他参数同模锻圆柱齿轮;D1≈1.6dk;D2≈da-10m(或mn)(且δ0≥10mm);当b=(1~1.5)dk时,取L=b,否则L=(1.2-1.5)dk;c=(0.2~0.3)b;D0≈0.5(D1+D2);d0=0.25(D2-D1);r=0.5c;n=0.5m(或mn)。
2.图b)D1≈1.6dk;L=(1.2~1.5)dk;δ0=(3~4)m,但不小于10mm;c=(0.1~0.17)R;D0、d0由结构设计确定。
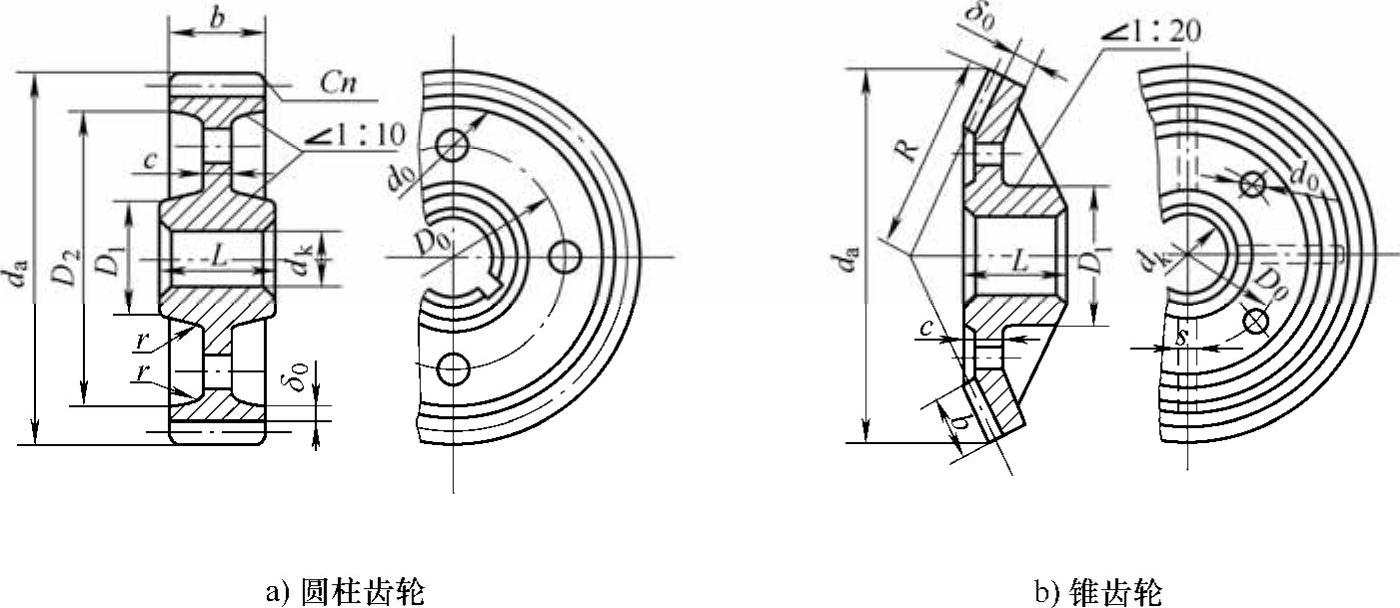
图6-43 腹板式铸造齿轮结构
注:1.图a)D1=1.6dk(铸钢),D1=1.8dk(铸铁);L=(1.2~1.5)dk(且L≥b); δ0=(2.5~4)m(或mn)(且δ0≥8~10mm);n=0.5m(或mn);r≈0.5c,c=0.2b≥10mm; D0=0.5(D1+D2);d0=0.25(D2-D1)。
2.图b)D1=1.6dk(铸钢),D1=1.8dk(铸铁);L=(1~1.2)dk;δ0=(3~4)m(且δ0≥10mm); c=(0.1~0.17)R≥10mm;s=0.8c≥10mm;D0、d0按结构确定。
(4)轮辐式结构齿轮 当400mm≤da≤1000mm时,顶圆直径超过了一般锻床的加工范围,因此齿轮常采用铸铁或铸钢制成,并采用轮辐式结构(见图6-44)。
(5)组合式结构齿轮 有时为了节约贵重金属,对于大尺寸的圆柱齿轮可采用组装结构,即齿圈采用贵重金属制造,齿芯可采用铸铁或铸钢(见图6-45)。
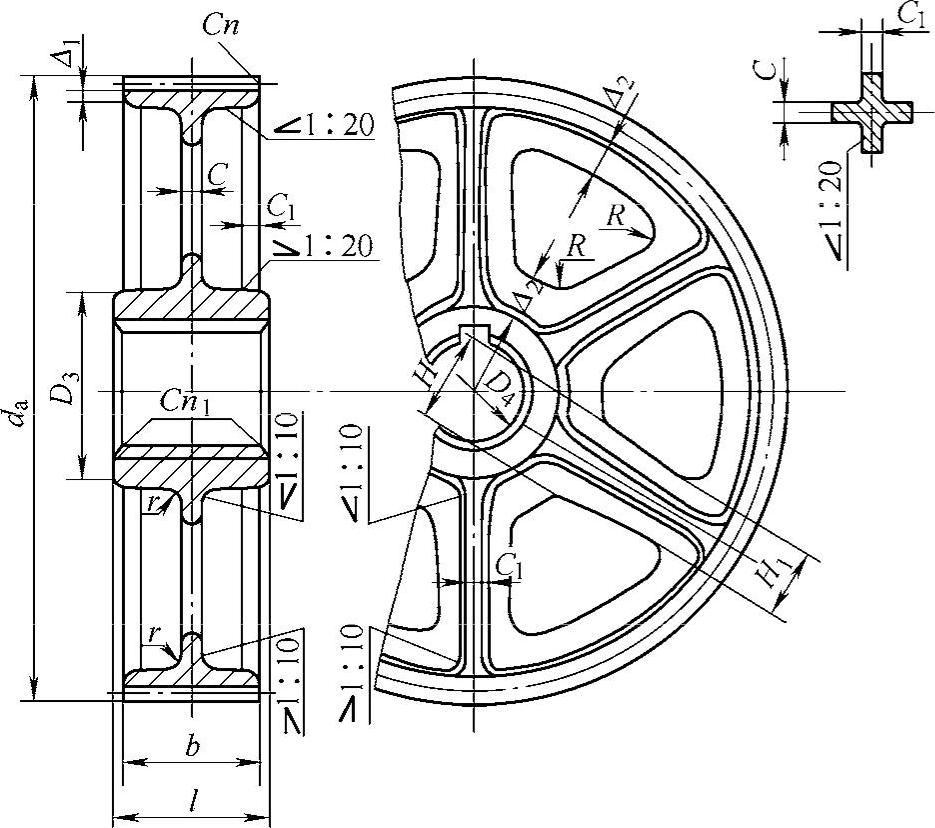
图6-44 轮辐式结构齿轮
注:b<240mm;D3=1.6D4(铸钢);D3=1.7D4(铸铁);Δ1≈(3~4)mn,但不小于8mm;Δ2=(1~1.2)Δ1;
H=0.8D4(铸钢);H=0.9D4(铸铁);H1=0.8H;C=H/5;C1=H/6;R=0.5H;1.5D4>l≥b。
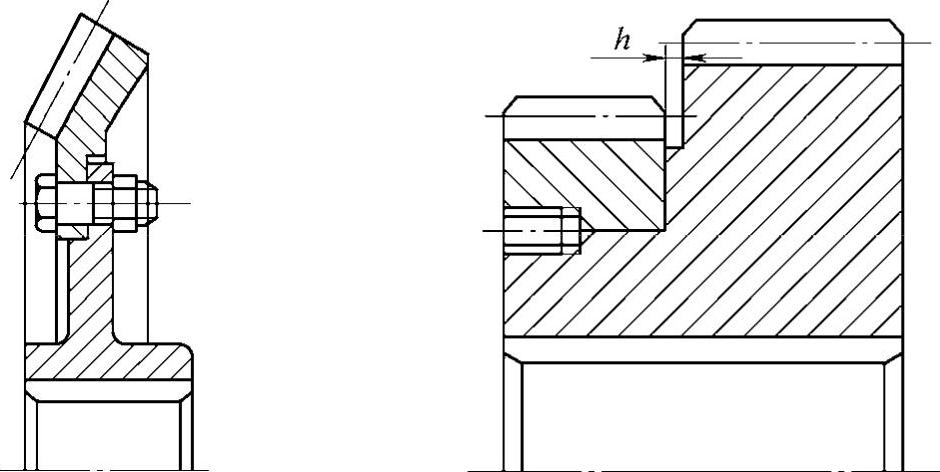
图6-45 组合式结构齿轮
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






